Método de bisección

Unas cuantas iteraciones del método de bisección aplicadas en un intervalo [a₁;b₁]. El punto rojo es la raíz de la función.

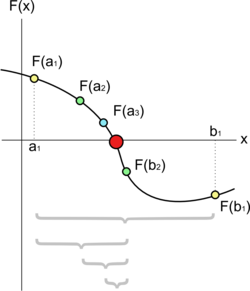
En matemáticas, el método de bisección es un algoritmo de búsqueda de raíces que trabaja dividiendo el intervalo a la mitad y seleccionando el subintervalo que tiene la raíz.

Introducción

Supóngase que queremos resolver la ecuación f(x) = 0 (donde f es continua. Dados dos puntos a y b tal que f(a) y f(b) tengan signos distintos, sabemos por el Teorema de Bolzano que f debe tener, al menos, una raíz en el intervalo [a, b]. El método de bisección divide el intervalo en dos, usando un tercer punto c = (a+b) / 2. En este momento, existen dos posibilidades: f(a) y f(c), ó f(c) y f(b) tienen distinto signo. El algoritmo de bisección se aplica al subintervalo donde el cambio de signo ocurre.

El método de bisección es menos eficiente que el método de Newton, pero es mucho más seguro asegurar la convergencia.

Si f es una función continua en el intervalo [a, b] y f(a)f(b) < 0, entonces este método converge a la raíz de f. De hecho, una cota del error absoluto es:

${\frac {\left|b-a\right|}{2^{n}}}$

en la n-ésima iteración. La bisección converge linealmente, por lo cual es un poco lento. Sin embargo, se garantiza la convergencia si f(a) y f(b) tienen distinto signo.

Si existieran más de una raíz en el intervalo entonces el método sigue siendo convergente pero no resulta tan fácil caracterizar hacia qué raíz converge el método.

Algoritmo

Para aplicar el método consideremos tres sucesiones $a_{n}\leq p_{n}\leq b_{n}\,$ definidas por las siguientes relaciones:

$p_{n}={\frac {a_{n}+b_{n}}{2}},\quad a_{n+1}={\begin{cases}a_{n}&{\mbox{si }}f(a_{n})\cdot f(p_{n})\leq 0\\p_{n}&{\mbox{si }}f(a_{n})\cdot f(p_{n})>0\end{cases}},\quad b_{n+1}={\begin{cases}p_{n}&{\mbox{si }}f(a_{n})\cdot f(p_{n})\leq 0\\b_{n}&{\mbox{si }}f(a_{n})\cdot f(p_{n})>0\end{cases}}$

Donde los valores iniciales vienen dados por:

$a_{0}:=a,\quad b_{0}:=b$

Se puede probar que las tres sucesiones convergen al valor de la única raíz del intervalo:

$\lim _{n\to \infty }a_{n}=\lim _{n\to \infty }p_{n}=\lim _{n\to \infty }b_{n}$

Método de bisección en diferentes lenguajes de Programación

C

El siguiente código en lenguaje C, Permite la obtención de de las raíces de una función usando el Método de bisección:

#include<stdio.h>
#include<math.h>
// #include<conio.h>                // NOTA: conio.h no es parte de ANSI C, es una libreria de C de Borland
//Funcion Que Queremos hallar
double f(double x){
   return ((pow(x/3, 2))+(9)); //Esta funcion es Y=(X*X*X)/3)+9 Reemplazar por la funcion deseada ej: Y=(x*x)+(3*x)+6
}

// Funcion pausar
char pausa()
{
     char c;
     printf("Presiona enter para contiuar...");
     c=getchar();
}

//biseccion: Retorna el valor de la funcion usando metodo de biseccion
//parametros: a= valor menor al punto
//parametros: b= valor mayor al punto
//parametros: p= el punto que deseamos encontrar
//parametros: errorDeseado = margen de error
double biseccion(double a, double b, double p, double errorDeseado){
   double xr, errorAbsoluto; //xr representa el punto intermedio
   printf("valor a:%f valorb:%f\n",a,b);
   xr=((b+a)/2);
   printf("biseccion a,b: %f\n",f(xr));
   //Cambia A o B por el valor del punto dependiendo de cuales se encuentran en medio de p
   if(p<xr){
      b=xr;
   }else{
      a=xr;
   }
   //calcula el error relativo
   errorAbsoluto=fabs(f(p)-fabs(f(xr)));
   //Si el margen de error ya es valido retorna la funcion.
   if (errorAbsoluto<errorDeseado){
      return xr;
   }else{
      return biseccion(a,b, p, errorDeseado);
   }
}
int main(){
   printf("%f\n", biseccion(-424,146, 7, 0.02)); // introduce un rango amplio
   // getch();        // NOTA: Se recomienda para pausar crear su propia funciona de caracter para continuar, o usar la pausa nativa de OS.
   pausa();           // system("pause"); es otra opcion en sistemas windows.
   return 0;
}

MatLab

function  x = biseccion(fun,a,b,tol)
% Aproxima por el método  de la bisección una raíz de la ecuación fun(x)=0
disp('Método de la bisección');
u=feval(fun,a);
v=feval(fun,b);
n=1; 
if sign(u)==sign(v)
   disp('Error la función debe cambiar de signo en (a,b)');
end 
while ((b-a)*0.5>tol)
   c=(b+a)/2; w=feval(fun,c);
   disp(['n=', num2str(n)]);
   disp(['c=', num2str(c)]);
   disp(['f(c)=', num2str(w)]);
if sign(u)==sign(w)
	a = c; u=w;
else
	b=c; v=w;
end
	n=n+1;
end;
x=c

Python

# -*- coding: utf-8 -*-
from math import * //porque a miguel le gusta el pico.

ec=raw_input('De la funcion a resolver: ')
x1=float(raw_input('de el extremo inferior del intervalo aproximado: '))
x2=float(raw_input('de el extremo superior del intervalo aproximado: '))
errordeseado=float(raw_input('De el error deseado: '))

def f(x):
    return eval(ec)

while True:
    xmed=(x1+x2)/2
    if f(xmed)==0.0:
        break
    if (f(x1)*f(xmed))<0:
        x2=xmed
    else:
        x1=xmed
    error=abs(x2-x1)
    if error<errordeseado:
        break
print 'La raiz es',xmed

SciLab

El siguiente código para SciLab, Permite la obtención de de las raíces de una función usando el Método de bisección:

function  x = biseccion(LaFuncion,a,b,tolerancia)
disp('Método de la bisección');
u=evstr("LaFuncion(a)");
v=evstr("LaFuncion(b)");
n=1; 
disp(sign(u));
disp(sign(v));
if sign(u)==sign(v)
   disp('Error la La función debe cambiar de signo en (a,b)');
end 
while ((b-a)*0.5>tolerancia)
   c=(b+a)/2; 
   w=evstr("LaFuncion(c)");
   disp(['************ Paso :  ', string(n), '************'] );
   disp(['Valor c=', string(c)]);
   disp(['f(c)=', string(w)]);   
if sign(u)==sign(w)
	a=c; 
	u=w;
else
	b=c;
	v=w;
end
	n=n+1;
end;
disp('************* La Raiz : *************');
x=c;
endfunction;

Referencia

Bibliografía

• Richard L Burden, J. Douglas Faires (2000), "Numerical Analysis, (7th Ed)", Brooks/Cole. ISBN 0-534-38216-9.