Estado crítico (mecánica de suelos)

El suelo normalmente consolidado pasa a estado crítico a lo largo de la trayectoria de tensión en la superficie de Roscoe.  

La mecánica del suelo de estado crítico es el área de la mecánica del suelo que abarca los modelos conceptuales que representan el comportamiento mecánico de los suelos saturados remoldeados en base al concepto del Estado Crítico. 

Formulación 

El concepto de Estado Crítico es una idealización del comportamiento observado de las arcillas saturadas remoldeadas en un ensayo triaxial de compresión, y es asumido que aplica a suelos no alterados. Establece que los suelos y otros materiales granulares, si son continuamente distorsionados (cortados) hasta que fluyan como un fluido friccional, entraran en un estado crítico bien definido. Al inicio del estado crítico, las distorsiones por cortante $\ \varepsilon _{s}$ , ocurren sin ningún otro cambio en el esfuerzo efectivo promedio$\ p'$, esfuerzo desviador $\ q$ (o esfuerzo de cedencia, $\ \sigma _{y}$, en tensión uniaxial de acuerdo con el criterio de cedencia de von Mises), o volumen específico$\ \nu$:  

$\ {\frac {\partial p'}{\partial \varepsilon _{s}}}={\frac {\partial q}{\partial \varepsilon _{s}}}={\frac {\partial \nu }{\partial \varepsilon _{s}}}=0$

Donde, 

$\ \nu =1+e$

$\ p'={\frac {1}{3}}(\sigma _{1}'+\sigma _{2}'+\sigma _{3}')$

$\ q={\sqrt {\frac {(\sigma _{1}'-\sigma _{2}')^{2}+(\sigma _{2}'-\sigma _{3}')^{2}+(\sigma _{1}'-\sigma _{3}')^{2}}{2}}}$

Sin embargo, para las condiciones de compresión triaxial $\ \sigma _{2}'=\sigma _{3}'$. Entonces,

$\ p'={\frac {1}{3}}(\sigma _{1}'+2\sigma _{3}')$

$\ q=(\sigma _{1}'-\sigma _{3}')$

Todos los estados críticos, para un suelo dado, forman una línea única llamada la Línea del Estado Crítico (CSL) definida por las siguientes ecuaciones en el espacio \ (p',q,v):  

$\ q=Mp'$

$\ \nu =\Gamma -\lambda \ln(p')$

donde $\ M$, $\ \Gamma$, and $\ \lambda$ son constantes del suelo. La primera ecuación determina la magnitud del esfuerzo desviador $\ q$  necesario para mantener el suelo fluyendo continuamente como el producto de una constante friccional $\ M$ (mayúscula$\ \mu$) y el esfuerzo efectivo promedio $\ p'$. La segunda ecuaciones establece que el volumen específico$\ \nu$  ocupado por unidad de volumen de las partículas que fluyen disminuirá mientras el logaritmo del esfuerzo efectivo promedio aumenta.  

Historia 

En un intento de técnicas de ensayos avanzados de suelos, Kenneth Harry Roscoe de la Universidad de Cambridge, a finales de los años 40 y principios de los 50, desarrolló un aparato de cortante simple en el que sus estudiantes posteriores intentaron estudiar los cambios en las condiciones en la zona de cortante, tanto en arena como en suelos arcillosos. En 1958 un estudio de la cedencia del suelo basado en algunos datos de Cambridge del ensayo en el aparato de cortante simple, y en muchos más datos de ensayos triaxiales en el Colegio Imperial de Londres de la investigación liderada por el profesor Sir Alex Skempton en los Laboratorios Imperiales de Geotecnia, llevó a la publicación del concepto de estado crítico (Roscoe, Schofield & Wroth 1958). 

Roscoe obtuvo su grado de licenciatura en ingeniería mecánica[1] y sus experiencias tratando de crear túneles para escapar cuando estuvo prisionero de guerra por los nazis durante la Segunda Guerra Mundial lo introdujeron a la mecánica de suelos.[1] Con posterioridad a su artículo de 1958, los conceptos de plasticidad fueron introducidos por Schofield (Schofield & Wroth 1968). Schofield fue alumno en Cambridge del profesor John Baker, un ingeniero estructural que era un ferviente creyente de las estructuras diseñadas que fallarían "plásticamente". Las teorías del profesor Baker influenciaron fuertemente el pensamiento de Schofield sobre el cortante de los suelos. Los puntos de vista de Baker fueron desarrollados desde su trabajo pre guerra en estructuras de acero y posteriormente informado por su experiencia en tiempos de guerra evaluando estructuras dañadas por explosiones y con el diseño del "Refugio Morrison", un refugio contra ataques aéreos el cual se podía colocar adentro (Schofield 2006).   

Modelo Cam-Clay original 

El modelo original Cam-Clay está basado en la asunción de que el suelo es isotrópico, elasto plástico y se deforma como un continuo, además no es afectado por el creep. La superficie de cedencia del modelo Cam Clay está descrita por la siguiente ecuación 

$f(p,q,p_{c})=q+M\,p\,\ln \left[{\frac {p}{p_{c}}}\right]\leq 0$

donde $q$ es el esfuerzo equivalente, $p$ es la presión, $p_{c}$ es la presión de preconsolidación, y $M$ es la pendiente de la línea de estado crítico en el espacio $p-q$

La presión de preconsolidación evoluciona como la razón de vacío (e) (y por lo tanto el volumen específico v) del suelo cambia. Una relación comúnmente usada es 

$e=e_{0}-\lambda \ln \left[{\frac {p_{c}}{p_{c0}}}\right]$

donde $\lambda$ es el índice de compresión virgen del suelo. Una limitación de este modelo es la posibilidad de volúmenes específicos negativos a valores de esfuerzo realistas. 

Una mejora para el modelo mencionado en $p_{c}$ es la forma bi-logarítmica 

$\ln \left[{\frac {1+e}{1+e_{0}}}\right]=\ln \left[{\frac {v}{v_{0}}}\right]=-{\tilde {\lambda }}\ln \left[{\frac {p_{c}}{p_{c0}}}\right]$

donde ${\tilde {\lambda }}$ es el índice de compresibilidad apropiado para el suelo.  

Superficie de cedencia en espacio p-q del Cam-clay 

Superficie de cedencia en espacio de esfuerzo principal del Cam-clay  

Modelo Cam-Clay modificado 

El profesor John Burland del Colegio Imperial, quien trabajó con el profesor Roscoe, está acreditado con el desarrollo de la versión modificada del modelo original. La diferencia entre el Cam Clay y el Cam Clay Modificado [2] (MCC) consiste en que la superficie de cedencia del MCC es descrita por una elipse, y por lo tanto el vector de incremento de la deformación plástica (el cual es perpendicular a la superficie de cedencia) para el valor más grande del esfuerzo efectivo promedio es horizontal, y por lo tanto ningún incremento de la deformación plástica desviatoria toma lugar para un cambia en el esfuerzo efectivo promedio (para estados de estrés puramente hidrostáticos). Esto es muy conveniente para el modelado constitutivo en un análisis numérico, especialmente en el análisis de elementos finitos, donde los problemas de estabilidad numérica son importantes (así como una curva necesita ser continua para ser diferenciable). 

La superficie de cedencia del Cam-clay modificado tiene la forma 

$f(p,q,p_{c})=\left[{\frac {q}{M}}\right]^{2}+p\,(p-p_{c})\leq 0$

donde $p$ es la presión, $q$ es el esfuerzo equivalente, $p_{c}$ es la presión de preconsolidación, y $M$ es la pendiente de la línea de estado crítico.   

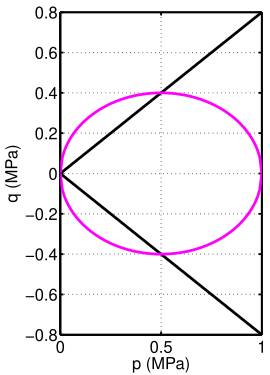
La superficie de cedencia del Cam-clay modificado en un espacio p-q  

Superficie de cedencia del Cam-clay modificado en un espacio de esfuerzo principal.  

Crítica 

Los conceptos básicos del acercamiento elastoplástico fueron primeramente propuestos por dos matemáticos, Daniel C. Drucker y William Prager (Drucker y Prager, 1952) en una nota corta de 8 páginas. [3] En su nota, Drucker y Prager también demostraron cómo usar su acercamiento para calcular la altura crítica de un banco vertical usando ya sea un plano o una superficie de falla log espiral. Su criterio de cedencia es hoy día llamado el Drucker-Prager criterio de cedencia. Su acercamiento fue subsecuentemente extendido por Kenneth H. Roscoe y otros en el departamento de mecánica de suelos de la Universidad de Cambridge. 

El estado crítico y la mecánica de suelos elastoplástica han sido tema de crítica desde que fueron introducidas. El factor clave que maneja la crítica es primariamente la asunción implícita de que los suelos están hechos de partículas puntuales isotrópicas. Los suelos reales están compuestos por partículas de tamaños finitos con propiedades anisotrópicas que fuertemente determinan el comportamiento observado. Consecuentemente, los modelos basados en una teoría basada en metales de plasticidad no son capaces de modelar el comportamiento de suelos que son el resultado de propiedades anisotrópicas de partículas, un ejemplo de esto es la caída de la resistencia cortante post pico, i.e., comportamiento deformación-suavizamiento. Debido a que estos modelos elastoplásticos de suelo  son únicamente capaces de modelar "curvas esfuerzo-deformación simples" como las de arcillas "gordas" isotrópicas y normal o ligeramente sobre consolidadas, i.e., tipos de suelo CL-ML constituidos de partículas de grano muy fino.    

También, en general, el cambio de volumen es gobernado por consideraciones de elasticidad y esta suposición siendo grandemente falsa para suelos reales, resulta en emparejamientos muy pobres de estos modelos a los cambios de volumen o cambios de presiones de poro. Además, los modelos elastoplásticos describen el elemento entero como un todo y no condiciones específicas directas en el plano de falla, como una consecuencia de que estos no modelas las curvas de esfuerzo-deformación post falla, particularmente para suelos que muestran deformación-suavizamiento post-pico. Finalmente, muchos modelos separan los efectos del esfuerzo hidrostático y el esfuerzo cortante, con cada uno asumiendo que provocan únicamente cambio de volumen y cambio de cortante respectivamente. En realidad, la estructura del suelo, siendo análoga a una "casa de naipes," muestra tanto la deformación cortante en la aplicación de una compresión pura, y los cambios de volumen en la aplicación de cortante puro.  

Críticas adicionales son que la teoría es "solamente descriptiva,"i.e., únicamente describe el comportamiento conocido y le falta la habilidad de explicar o predecir el comportamiento estándar del suelo como, por qué la relación de vacíos en un ensayo de compresión unidimensional varía linealmente con el logaritmo del esfuerzo efectivo vertical. Para este comportamiento, el estado crítico de la mecánica de suelos simplemente asume que está dado.  

Por estas razones, el estado crítico y la mecánica de suelos elastoplástica han sido tildadas de escolásticas; los ensayos para demostrar su validez son usualmente "ensayos de conformación" donde únicamente curvas de esfuerzo-deformación simple han sido modeladas satisfactoriamente. El estado crítico y los conceptos a su alrededor tienen una larga historia de ser "escolásticos," con Sir Alec Skempton, el "padre fundador" de la mecánica de suelos británica, atribuyendo la naturaleza escolástica de CSSM a Roscoe, de quien dijo: "...hizo muy poco trabajo de campo y creo yo que nunca estuvo involucrado en un trabajo práctico de ingeniería,"[4]. En 1960s y 1970s, el profesor Alan Bishop en el Colegio Imperial acostumbraba a demostrar la inhabilidad de estas teorías para emparejar las curvas esfuerzo-deformación de suelos reales. Joseph (2013) ha sugerido que el estado crítico y la mecánica de suelos elasto plásticas alcanzan el grado de un "programa de investigación degenerado", un concepto propuesto por el filósofo de la ciencia Imre Lakatos para teorías donde las excusas son usadas para justificar la inhabilidad de la teoría para emparejar los datos empíricos. [5]  

Respuesta 

Los reclamos de que el estado crítico de la mecánica de suelos es solo descriptivo y alcanza el criterio de programa de investigación degenerado no han sido establecidos. Andrew Jenike usó una relación logarítmica-logarítmica para describir el ensayo de compresión en su teoría del estado crítico y admitió reducciones en esfuerzo durante flujo convergente y aumentos en esfuerzo durante flujo divergente. [6] Chris Szalwinski definió un estado crítico como un estado multifase donde el volumen específico es el mismo en las fases sólidas y líquidas. [7] Según esta definición, la relación lineal-logarítmica de la teoría original y la teoría logarítmica-logarítmica de Jenike son casos especiales de un fenómeno físico más general.  

Referencias 

• Datos: Q5186771