Teorema del coseno

El objetivo de este apéndice es presentar pruebas de algunas afirmaciones usadas en el artículo Teorema del coseno, pero que por razones didácticas es preferible separar del cuerpo principal, ya que incluirlas directamente interrumpiría el flujo de la explicación con digresiones no relacionadas directamente con el tema central de la exposición.

Area de un paralelogramo

Deducción del teorema sobre área de un paralelogramo.

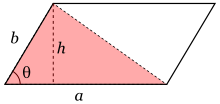
Se afirma:

Un paralelogramo cuyos lados miden a y b, formando un ángulo de 90°-γ, tiene un área de ab cos(γ).

Consideremos un paralelogramo de lados a y b, formando un ángulo de θ, como n el diagrama. Dividamos el paralelogramo por medio de una diagonal para obtener dos zonas triangulares. En una de ellas, dibujemos una altura h como se muestra en la figura.

La zona triangular roja tiene por área ah/2. Por definición, sin(θ)=h/b, de modo que h=b sin(θ). La sustitución en la fórmula del área triangular prueba que:

El área de un triángulo en donde dos lados de medidas a y b forman un ángulo de θ es $A_{T}={\frac {ab\,\cos \theta }{2}}$

Dado que el área del paralelogramo es el doble del triángulo, se concluye que

El área de un paralelogramo de lados a y b formando un ángulo de θ es $A_{P}=ab\,\cos \theta$

La conclusión se sigue notando que si θ=90-γ entonces sen(θ)=sen(90°-γ) = cos(γ). Se hace notar también que la demostración es independiente de cual de las diagonales del paralelogramo se escoja, puesto que sen(θ)=sen(180°-θ).

Cuerdas en un círculo

Diagrama usado en la prueba basada en potencia de un punto

En la demostración del Teorema del coseno usando potencia de un punto, se afirma que el segmento CK en el diagrama mide precisamente -2a cos(γ).

La demostración más sencilla consiste en prolongar el segmento CB hasta cortar nuevamente la circunferencia en un punto D, de modo que CD es un diámetro del círculo, puesto que pasa por el centro del mismo.

Al ser un diámetro, el ángulo inscrito CKD es necesariamente recto por lo que el triángulo CKD es rectángulo. El ángulo DCK mide θ=180°-γ y por definición:

$\cos(\theta )={\frac {CK}{CD}}={\frac {CK}{2a}}$

y por tanto

$CK=2a\cos(\theta )=2a\cos(180^{\circ }-\gamma )=-2a\cos(\gamma )$

ya que cos(180°-x) = -cos(x) para cualquier valor de x.