Problema de transporte

Un problema de transporte​ es, en matemáticas y economía, un caso particular de problema de programación lineal en el cual se debe minimizar el coste del abastecimiento a una serie de puntos de demanda a partir de un grupo de puntos de oferta —posiblemente de distinto número—, teniendo en cuenta los distintos precios de envío de cada punto de oferta a cada punto de demanda.

Planteamiento

Se disponen $n\in \mathbb {N}$ puntos de oferta o factorías con una producción determinada (representada mediante un vector, F) y $m\in \mathbb {N}$ puntos de demanda o mercados de demanda determinada (vector M):

$F\in \mathbb {R} ^{n};\;F=(F_{1},F_{2},F_{3},\cdots ,F_{n})$

$M\in \mathbb {R} ^{m};\;M=(M_{1},M_{2},M_{3},\cdots ,M_{m})$

Además se dispone como dato de una matriz de precios, C, de forma que $C_{ij}$ es el precio de envío por unidad desde la factoría $F_{i}$ al mercado $M_{j}$:

$C\in {\mathcal {M}}_{n\times m}(\mathbb {R} )$

El objetivo es calcular una nueva matriz, X, de forma que $X_{ij}$ sea el número de unidades que se envían de la factoría $F_{i}$ al mercado $M_{j}$.

$X\in {\mathcal {M}}_{n\times m}(\mathbb {R} )$

Con estos datos podemos formular las condiciones que se han de cumplir:

$\sum _{i=1}^{n}X_{ij}\geq M_{j}\;\;\forall j\in \mathbb {N} /1\leq j\leq m$

$\sum _{j=1}^{m}X_{ij}\leq F_{i}\;\;\forall i\in \mathbb {N} /1\leq i\leq n$

$X_{ij}\geq 0\;\;(i,j\in \mathbb {N} ;1\leq i\leq n;1\leq j\leq m)$

El precio total a pagar por el transporte, $C_{T}$, que se ha de minimizar, se determinará por la suma de los productos del precio de cada unidad por el coste de envío por unidad de cada fábrica a cada mercado:

$C_{T}=\sum _{i=1}^{n}\sum _{j=1}^{m}X_{ij}\cdot C_{ij}$

$\min \;C_{T}$

Problemas equilibrados​

Se dice que el problema está equilibrado cuando se cumple que:

$\sum _{i=1}^{n}F_{i}=\sum _{j=1}^{m}M_{j}$

(o, abreviadamente, $\sum F=\sum M$, es decir, la oferta total es igual a la demanda total).

En caso de que $\sum F>\sum M$ (Oferta total sea mayor a la demanda total) se incorporaría un centro de consumo adicional al problema, el centro de consumo artificial, $M_{a}$, de forma que su demanda sea el excedente ( $M_{a}=\sum F-\sum M$) y el coste de envío a este mercado sea nulo:

$C_{ia}=0\;\;\forall i\in \mathbb {N} /1\leq i\leq n$.

En caso de que $\sum F<\sum M$ (Demanda total mayor a la oferta total) se incorporaría una factoría adicional al problema, la factoría artificial, $M_{b}$, de forma que su oferta sea el excedente ($M_{b}=\sum M-\sum F$ ) y el coste de envío de esta factoría sea nulo:

$C_{bj}=0\;\;\forall j\in \mathbb {N} /1\leq j\leq m$.

Representación Gráfica del Problema de Transporte

Se muestra la presentación gráfica del problema de transporte donde:

Representación Gráfica del Problema de Transporte

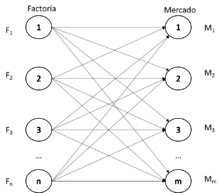
• Nodos: Factorías y Mercados. A cada nodo se le asocia una restricción con su oferta Fi y demanda Mj.
• Arcos: Ruta a seguir para transportar las mercancías. A cada arco se le asocia una variable de decisión $X_{i,j}$.

Tabla de Transporte

La estructura del problema de transporte permite una representación compacta del problema utilizando el formato de tabla de transporte como se muestra a continuación.​

	Mercado 1	Mercado 2		Mercado j		Mercado m
Factoría 1	costo(1, 1)	costo(1, 2)	...	costo (1, j)	...	costo(1, m)	Oferta 1 ($F_{1}$)
Factoría 2	costo(2,1)	costo(2,2)	...	costo (2, j)	...	costo(2, m)	Oferta 2 ($F_{2}$)
...	...	...	...	...	...	...	...
Factoría i	costo (i,1)	costo (i,2)	...	costo(i,j)	...	costo(i,m)	Oferta i ($F_{i}$)
...	...	...	...	...	...	...	...
Factoría n	costo(n, 1)	costo(n,2)	...	...	...	costo(n, m)	Oferta n ($F_{n}$)
	Demanda 1 ($M_{1}$)	Demanda 2 ($M_{2}$)	...	Demanda j ($M_{j}$)		Demanda m ($M_{m}$)

Cabe mencionar que los costes deben ser colocados en la esquina superior derecha.

Comparación entre los planteamientos

Entre cada representación existe una equivalencia que se menciona a continuación:

Modelo de Programación Lineal	Gráfica	Tabla de Transporte	Número
Restricción	Nodo	Renglón (oferta) o columna (demanda)	n+m
Variable $X_{i,j}$	Arco	Casilla	nm

Solución del Problema de Transporte

El problema de transporte puede ser resuelto de las siguientes formas:

• Método Simplex: El problema de transporte puede ser resuelto planteando el modelo de programación lineal y utilizar ya sea el método de la gran M o el método de las dos fases (métodos variantes del método simplex).
• Técnica de Transporte: Consta de los mismos pasos del método simplex sin embargo es una técnica específica de solución.

Para que un problema de transporte pueda ser resuelto a través de la técnica de transporte debe cumplir con las características:

• Ser un problema equilibrado (la oferta total y la demanda total deben ser igual).
• Contar con $n+m-1$ variables básicas, siendo $n$ los puntos de demanda y $m$ los puntos de oferta.

Técnica de Transporte

Para aplicar la técnica de transporte se utiliza la tabla de transporte equilibrada. Los pasos son los mismos del método simplex, los cuales contemplan:

• Establecer solución básica factible inicial:

Existen varios métodos para hacer esto: Noreste y sus variaciones(Suroeste, Suroeste, etc), y Costo mínimo o el método de Vogel:​ Con cualquiera de estos métodos se debe obtener una solución que contemple $n+m-1$ variables básicas.

• Definir la variable de entrada:

Para encontrar la variable de entrada se utilizará los criterios ya establecidos del método simplex para un caso minimizado. Y se encontrará la variable utilizando el método de multiplicadores o método de u-v. Dicho método utiliza el modelo dual del modelo de programación lineal. El método calcula los valores de las variables duales $u_{i}$ y $v_{j}$ (cada renglón tendrá un $u_{i}$ y cada columna tendrá un $v_{j}$). Estos multiplicadores se obtienen de las ecuaciones: $u_{i}+v_{j}=c_{i,j}$ para cada variable básica $x_{i,j}$

En total se tendrán n+m-1 ecuaciones y m+n multiplicadores. Es necesario utilizar un valor arbitrario para uno de ellos y de ahí encontrar los demás valores de los multiplicadores.

Para encontrar el $z_{j}-c_{j}$ de las variables no básicas se utiliza la relación:

Suponga que $x_{s,r}$ es la variable no básica, entonces se calcula con $u_{s}+v_{r}-c_{s,r}$.

Si al calcular estos valores alguno es positivo, se elige al valor más grande del $z_{j}-c_{j}$ como la variable de entrada. En el caso de que todos sean $z_{j}-c_{j}<0$, entonces la solución actual es la óptima.

• Establecer la variable de salida

Para identificar la variable de salida será necesario construir un circuito. Los circuitos se construyen a partir de la solución básica factible. Un circuito debe contener únicamente variables básicas con excepción de la variable de entrada. Suponga un ejemplo con la siguiente tabla con 3 factorías y 4 mercados, en este caso se tendrán 6 variables básicas (3+4-1) y una posible solución inicial podría ser (se pone B para indicar que es variable básica):

	Mercado 1	Mercado 2	Mercado 3	Mercado 4
Factoría 1	B	B
Factoría 2		B	B	B
Factoría 3				B

Suponga que la variable entrada es la casilla (3,1), esta variable deberá tomar un valor de $+\nu$, esto ocasiona un reajuste de las demás casillas básicas, el análisis se realiza por columna y por renglón, por tanto el reajuste será:

	Mercado 1	Mercado 2	Mercado 3	Mercado 4
Factoría 1	B$-\nu$	B$+\nu$
Factoría 2		B$-\nu$	B	B$+\nu$
Factoría 3	$+\nu$			B$-\nu$

Para determinar el valor de la variable de entrada $x_{i,j}$ y establecer la variable de salida:

$x_{i,j}=min\left\{X_{p,q}/X_{p,q}-\nu \ X_{p,q}b{\acute {a}}sica\right\}$

En este caso el valor de la variable de entrada $\nu$ se encuentra en los valores de las casillas (1,1), (2,2) y (3,4) de estos se elige el valor más pequeño (esta casilla será la variable de salida). Una vez que se tenga el valor $\nu$ se hace las sumas y las restas de las demás casillas del circuito. Se regresa al paso de la variable de entrada.

Véase también

• Problema del viajante
• Movilidad de último kilómetro

Bibliografía

• Hillier, F. S., Lieberman, G. J., & Elmer, M. M. (2006). Introducción a la Investigación de Operaciones. México, D.F.: McGraw-Hill.
• Taha, H. A. (2011). Operations research: An introduction. Upper Saddle River, NJ: Prentice Hall.
• Winston, W. L., & Goldberg, J. B. (2004). Investigación de Operaciones: Aplicaciones y algoritmos. Australia: Thomson.

• Datos: Q1929885
• Multimedia: Transportation theory / Q1929885