Grafo cactus

De Wikipedia, la enciclopedia libre
Un grafo cactus

En teoría de grafos, un cactus (a veces llamado árbol de cactus) es un grafo conectado en el que dos ciclos simples tienen como máximo un vértice en común. De manera equivalente, es un grafo conectado en el que cada arista pertenece a un ciclo simple como máximo, o (para cactus no triviales) en el que cada bloque (subgrafo máximo sin vértices de corte) es una arista o un ciclo.

Propiedades[editar]

Los grafos cactus son plano exteriores. Cada seudoárbol es un cactus. Un grafo no trivial es un cactus si y solo si cada unos de sus bloques es un ciclo simple o una sola arista.

La familia de grafos en los que cada componente es un cactus es cerrada hacia abajo respecto a las operaciones de determinación de menores. Esta familia de grafos se puede caracterizar por un solo menor prohibido, el grafo diamante de cuatro vértices formado al eliminar un borde del grafo completo K4.[1]​

Cactus triangular[editar]

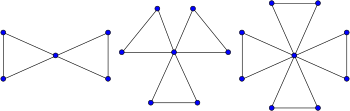
Los grafos de la amistad son cactus triangulares

Un cactus triangular es un tipo especial de grafo cactus en el que cada ciclo tiene una longitud de tres y cada arista pertenece a un ciclo. Por ejemplo, los grafos de la amistad, grafos formados a partir de una colección de triángulos unidos en un solo vértice compartido, son cactus triangulares. Además de ser grafos de cactus, los cactus triangulares también son grafos bloque y localmente lineales.

Los cactus triangulares tienen la propiedad de permanecer unidos si se les quita algún emparejamiento; para un número dado de vértices, tienen la menor cantidad posible de aristas con esta propiedad. Cada árbol con un número impar de vértices puede convertirse en un cactus triangular añadiéndole aristas, dando un aumentado mínimo con la propiedad de permanecer conectado después de la eliminación de un emparejamiento.[2]​

El cactus triangular más grande en cualquier grafo se puede encontrar en tiempo polinómico usando un algoritmo para el problema de la paridad de matroides. Dado que los grafos cactus triangulares son planos, el cactus triangular más grande se puede usar como una aproximación al subgrafo plano más grande, un subproblema importante en planarización. Como algoritmo de aproximación, este método tiene algoritmo de aproximación 4/9, el más conocido para el problema del subgrafo plano máximo.[3]​

El algoritmo para encontrar el cactus triangular más grande está asociado con un teorema de Lovász y Plummer que caracteriza el número de triángulos en este cactus más grande.[4]​ Lovász y Plummer consideran pares de particiones de vértices y aristas del grafo dado en subconjuntos, con la propiedad de que cada triángulo del grafo tiene dos vértices en una sola clase de partición de vértices o las tres aristas en una sola clase de grafo de partición de arista; llaman a un par de particiones con esta propiedad "válidas".

Entonces, el número de triángulos en el cactus triangular más grande es igual al máximo, sobre pares de particiones válidas y , de

,

donde es el número de vértices en el grafo dado y es el número de clases de vértices que cumple la clase de arista .

Recientemente, se probó un límite extremo estrecho[5]​ que demostraba que dado cualquier grafo plano , siempre existe un subgrafo de cactus que contiene al menos la fracción de las caras triangulares de . Este resultado implica un análisis directo del algoritmo de aproximación 4/9 para el problema del subgrafo plano máximo sin usar la fórmula mín-máx anterior.

Conjetura de Rosa[editar]

Una conjetura importante relacionada con el cactus triangular es la conjetura de Rosa, llamada así por Alexander Rosa, que dice que todos los cactus triangulares son elegantes o casi elegantes.[6]​ Más precisamente

En todos los cactus triangulares con t ≡ 0, los 1 mod 4 bloques son elegantes, y en aquellos con t ≡ 2, los 3 mod 4 bloques son casi elegantes.

Algoritmos y aplicaciones[editar]

Algunos problemas de ubicación de instalaciones que son de dificultad NP para grafos generales, así como algunos otros problemas de grafos, pueden resolverse en tiempo polinómico en el caso de los grafos cactus.[7]​[8]​

Dado que los cactus son casos especiales de grafos planos exteriores, se pueden resolver varios problemas de optimización combinatoria en grafos en tiempo polinómico.[9]​

Los grafos cactus representan circuitos que tienen propiedades útiles. Una de sus primeras aplicaciones se asoció con la representación de amplificadores operacionales.[10]​[11]​[12]​

También se han utilizado en genómica comparativa como una forma de representar la relación entre diferentes genomas o partes de genomas.[13]​

Si un grafo cactus está conectado, y cada uno de sus vértices pertenece como máximo a dos bloques, entonces se llama cactus de Navidad. Cada grafo poliédrico tiene un subgrafo de cactus navideño que incluye todos sus vértices, un hecho que juega un papel esencial en una prueba de Leighton y Moitra (2010) de que cada grafo poliédrico tiene un embebido ávido en un espacio bidimensional, una asignación de coordenadas a los vértices para los cuales un procedimiento de reenvío ávido logra enrutar mensajes entre todos los pares de vértices.[14]​

En teoría de grafos topológica, los grafos cuyos embebidos celulares son todos planos son exactamente la subfamilia de los grafos de cactus con la propiedad adicional de que cada vértice pertenece como máximo a un ciclo. Estos grafos tienen dos menores prohibidos, el grafo de diamante y el grafo de la amistad de cinco vértices.[15]​

Historia[editar]

Los grafos cactus se estudiaron por primera vez con el nombre de árboles de Husimi, término ideado por Frank Harary y George Eugene Uhlenbeck en honor al trabajo previo de Kôdi Husimi en estos grafos.[16]​[17]​ El mismo artículo de Harary-Uhlenbeck reservaba el nombre de cactus para grafos de este tipo en los que cada ciclo es un triángulo, pero posteriormente se permiten ciclos de cualquier longitud como estándar.

Mientras tanto, el nombre árbol de Husimi comúnmente vino a referirse a grafos en los que cada bloque es un grafo completo (equivalentemente, los grafos de intersección de los bloques en algún otro grafo). Este uso tuvo poco que ver con el trabajo de Husimi, y ahora se usa el término más pertinente grafo bloque para esta familia. Sin embargo, debido a esta ambigüedad, esta frase se usa con menos frecuencia para referirse a los grafos de cactus.[18]​

Referencias[editar]

  1. ↑ El-Mallah, Ehab; Colbourn, Charles J. (1988), «The complexity of some edge deletion problems», IEEE Transactions on Circuits and Systems 35 (3): 354-362, doi:10.1109/31.1748 .
  2. ↑ Farley, Arthur M.; Proskurowski, Andrzej (1982), «Networks immune to isolated line failures», Networks 12 (4): 393-403, MR 686540, doi:10.1002/net.3230120404 .
  3. ↑ Călinescu, Gruia; Fernandes, Cristina G; Finkler, Ulrich; Karloff, Howard (2002), «A Better Approximation Algorithm for Finding Planar Subgraphs», Journal of Algorithms, 2 27 (2): 269-302, S2CID 8329680, doi:10.1006/jagm.1997.0920, «citeseerx: 10.1.1.47.4731» .
  4. ↑ Lovász, L.; Plummer, M.D. (2009), Matching Theory, AMS Chelsea Publishing Series, ISBN 9780821847596 .
  5. ↑ Chalermsook, Parinya; Schmid, Andreas; Uniyal, Sumedha (2019), «A tight extremal bound on the Lovász cactus number in planar graphs», en Niedermeier, Rolf; Paul, Christophe, eds., 36th International Symposium on Theoretical Aspects of Computer Science, STACS 2019, March 13-16, 2019, Berlin, Germany, LIPIcs 126, Schloss Dagstuhl - Leibniz-Zentrum für Informatik, pp. 19:1-19:14, arXiv:1804.03485, doi:10.4230/LIPIcs.STACS.2019.19 .
  6. ↑ Rosa, A. (1988), «Cyclic Steiner Triple Systems and Labelings of Triangular Cacti», Scientia 1: 87-95 ..
  7. ↑ Ben-Moshe, Boaz; Bhattacharya, Binay; Shi, Qiaosheng (2005), «Efficient algorithms for the weighted 2-center problem in a cactus graph», Algorithms and Computation, 16th Int. Symp., ISAAC 2005, Lecture Notes in Computer Science 3827, Springer-Verlag, pp. 693-703, ISBN 978-3-540-30935-2, doi:10.1007/11602613_70 .
  8. ↑ Zmazek, Blaz; Zerovnik, Janez (2005), «Estimating the traffic on weighted cactus networks in linear time», Ninth International Conference on Information Visualisation (IV'05), pp. 536-541, ISBN 978-0-7695-2397-2, S2CID 15963409, doi:10.1109/IV.2005.48 .
  9. ↑ Korneyenko, N. M. (1994), «Combinatorial algorithms on a class of graphs», Discrete Applied Mathematics 54 (2–3): 215-217, doi:10.1016/0166-218X(94)90022-1. . Translated from Notices of the BSSR Academy of Sciences, Ser. Phys.-Math. Sci., (1984) no. 3, pp. 109-111 (en ruso)
  10. ↑ Nishi, Tetsuo; Chua, Leon O. (1986), «Topological proof of the Nielsen-Willson theorem», IEEE Transactions on Circuits and Systems 33 (4): 398-405, doi:10.1109/TCS.1986.1085935 .
  11. ↑ Nishi, Tetsuo; Chua, Leon O. (1986), «Uniqueness of solution for nonlinear resistive circuits containing CCCS's or VCVS's whose controlling coefficients are finite», IEEE Transactions on Circuits and Systems 33 (4): 381-397, doi:10.1109/TCS.1986.1085934 .
  12. ↑ Nishi, Tetsuo (1991), «On the number of solutions of a class of nonlinear resistive circuit», Proceedings of the IEEE International Symposium on Circuits and Systems, Singapore, pp. 766-769 .
  13. ↑ Paten, Benedict; Diekhans, Mark; Earl, Dent; St. John, John; Ma, Jian; Suh, Bernard; Haussler, David (2010), «Cactus Graphs for Genome Comparisons», Research in Computational Molecular Biology, Lecture Notes in Computer Science 6044, pp. 410–425, ISBN 978-3-642-12682-6, doi:10.1007/978-3-642-12683-3_27 .
  14. ↑ Leighton, Tom; Moitra, Ankur (2010), «Some Results on Greedy Embeddings in Metric Spaces», Discrete & Computational Geometry 44 (3): 686-705, S2CID 11186402, doi:10.1007/s00454-009-9227-6 ..
  15. ↑ Nordhaus, E. A.; Ringeisen, R. D.; Stewart, B. M.; White, A. T. (1972), «A Kuratowski-type theorem for the maximum genus of a graph», Journal of Combinatorial Theory, Series B 12 (3): 260-267, MR 0299523, doi:10.1016/0095-8956(72)90040-8 .
  16. ↑ Harary, Frank; Uhlenbeck, George E. (1953), «On the number of Husimi trees, I», Proceedings of the National Academy of Sciences 39 (4): 315-322, Bibcode:1953PNAS...39..315H, MR 0053893, PMC 1063779, PMID 16589268, doi:10.1073/pnas.39.4.315 .
  17. ↑ Husimi, Kodi (1950), «Note on Mayers' theory of cluster integrals», Journal of Chemical Physics 18 (5): 682-684, Bibcode:1950JChPh..18..682H, MR 0038903, doi:10.1063/1.1747725 .
  18. ↑ See, e.g., MR 0659742, a 1983 review by Robert E. Jamison of a paper using the other definition, which attributes the ambiguity to an error in a book by Mehdi Behzad and Gary Chartrand.

Enlaces externos[editar]

Obtenido de «https://es.wikipedia.org/w/index.php?title=Grafo_cactus&oldid=145997453»