Problema de los 100 prisioneros

En el dilema de los 100 prisioneros, cada prisionero debe encontrar su número en uno de los 100 cajones, pero cada uno sólo puede abrir 50 cajones.

El dilema de los 100 prisioneros y 100 cajones es un problema en la teoría de la probabilidad y la combinatoria. Consiste en que cada uno de 100 prisioneros debe encontrar su número en uno de los 100 cajones para sobrevivir y si alguno no lo encuentra, todos morirán; y, cada prisionero puede abrir sólo 50 cajones y no puede comunicarse con los demás prisioneros, excepto en el debate previo de la estrategia.

A primera vista, la situación es desesperada, pero existe una estrategia que ofrece a los cautivos una oportunidad de supervivencia aproximadamente del 30%. El científico en computación danés Peter Bro Miltersen fue el primero en proponer este problema en el 2003.

Problema

En la literatura se encuentran diferentes enunciados de este problema. A continuación se muestra la versión de Philippe Flajolet y Robert Sedgewick:

El director de una prisión ofrece a un centenar de condenados a muerte (numerados del 1 al 100) una última oportunidad. En una sala hay un armario con 100 cajones. El director coloca aleatoriamente en cada cajón uno de los números de 1 a 100. Los prisioneros entran en la sala, uno tras otro. Cada uno de los prisioneros puede: abrir y comprobar sólo 50 cajones en cualquier orden, y después cierra todos los cajones. Si en esta búsqueda todos los prisioneros han encontrado respectivamente su número, todos los prisioneros son perdonados; si un prisionero no encontrara su número, todos los prisioneros serán ejecutados. Antes de que el primer prisionero busque su número, los prisioneros pueden discutir la estrategia, pero no pueden comunicarse a partir de este momento. ¿Cuál es la mejor estrategia de los prisioneros? ^{[cita requerida]}

Si el prisionero selecciona 50 cajones de 100 al azar, la probabilidad de que encuentre su número es el 50%. La probabilidad de que todos los prisioneros, buscando aleatoriamente en los cajones de dicho armario, encuentren sus números, es el producto de la probabilidad de éxito individual de cada prisionero, es decir, (1/2)¹⁰⁰ ≈ 0,0000000000000000000000000000008, un número significativamente pequeño. La situación parece desesperada.

Solución

La estrategia

Sorprendentemente existe una estrategia que proporciona la probabilidad de supervivencia de más del 30%. La clave del éxito radica en el hecho de que los prisioneros no necesitan decidir de antemano cuáles cajones abrir: cada prisionero puede utilizar la información recibida del contenido de los cajones ya abiertos, para decidir cuál abrir después. Otra importante observación es que el éxito de un prisionero no es independiente del éxito de otros prisioneros, ya que todo depende de cómo se distribuyeron los números en los cajones.

La estrategia descrita cubre no sólo los prisioneros, sino también los cajones numerados del 1 al 100 (por ejemplo, hilera por hilera, a partir del primer cajón de la esquina superior izquierda del armario). La estrategia a seguir es:

1. Cada prisionero, primero abre el cajón con su número.
2. Si este cajón contiene su número, el prisionero ha concluido con éxito.
3. En caso contrario, el cajón contiene un número de otro prisionero, y se abre el cajón con dicho número.
4. El prisionero repite los pasos 2 y 3 hasta que encuentre su número o hasta abrir los 50 cajones.

Comenzando con su propio número el prisionero se garantiza de seguir una secuencia de apertura de cajones en el que pueda finalmente encontrar su número. La única cuestión reside en si la secuencia es mayor de 50.

Ejemplos

La razón del éxito de esta estrategia puede ilustrarse en el siguiente ejemplo, usando 8 prisioneros y 8 cajones, cada prisionero puede abrir 4 cajones. Supongamos que el director ha distribuido los números de prisioneros aleatoriamente en cada cajón de la siguiente manera:

número de cajón	1	2	3	4	5	6	7	8
número de prisionero	7	4	6	8	1	3	5	2

De acuerdo con la anterior estrategia, los prisioneros deben actuar de la siguiente manera:

1. El prisionero 1, en primer lugar abre el cajón 1 y encuentra en el número 7. A continuación, abre el cajón 7 y encuentra el número 5. A continuación, abre el cajón 5, donde encuentra su número y por lo tanto termina con éxito.
2. El prisionero 2 abre por orden los cajones 2, 4 y 8. En el último cajón encuentra su número.
3. El prisionero 3 abre los cajones de 3 y 6; en este último encuentra su número.
4. El prisionero 4 abre los cajones de 4, 8 y 2, antes de encontrar su número. Observe que es el mismo ciclo del prisionero número 2, aunque ninguno de estos prisioneros lo sabe.
5. Los prisioneros numerados del 5 al 8 también encontrarán sus números de igual manera.

En este ejemplo, todos los prisioneros encuentran sus números. Sin embargo, esto siempre no es así. Por ejemplo, si se cambia el contenido de los cajones 5 y 8, el prisionero 1 utiliza todos sus intentos, abriendo los cajones 1, 7, 5 y 2, y no encontrará su número:

número de cajón	1	2	3	4	5	6	7	8
número de prisionero	7	4	6	8	2	3	5	1

Y en la siguiente distribución, el prisionero 1 abriendo los cajones de 1, 3, 7 y 4, tampoco tendrá éxito:

número de cajón	1	2	3	4	5	6	7	8
número de prisionero	3	1	7	5	8	6	4	2

En realidad, en este ejemplo, todos los prisioneros, excepto el prisionero 6, fracasarán.

Esta estrategia se puede explicar a través de la permutación y de la teoría de la probabilidad

Representación de permutación

Representaciones de las permutaciones con grafos (1 7 5)(2 4 8)(3 6) y (1 3 7 4 5 8 2)(6)

La asignación por el director de los números de prisioneros a cada cajón se puede describir matemáticamente como una permutación de los números del 1 al 100. Dicha permutación es una aplicación biyectiva del conjunto de números naturales del 1 al 100 a sí mismo. Una secuencia de números que después de la aplicación repetida de la permutación vuelve al primer número se denomina ciclo de la permutación. Toda permutación puede descomponerse en ciclos disjuntos, es decir, ciclos que no tienen elementos comunes. La permutación del primer ejemplo anterior se puede escribir en notación cíclica como

$(1~7~5)(2~4~8)(3~6)$

y, por lo tanto, consta de dos ciclos de longitud 3 y un ciclo de longitud 2. La permutación del segundo ejemplo es, en consecuencia,

$(1~3~7~4~5~8~2)(6)$

y consiste en un ciclo de longitud 7 y un ciclo de longitud 1. La notación del ciclo no es única ya que un ciclo de longitud l se puede escribir en l diferentes formas dependiendo del número de inicio del ciclo. Durante la apertura de los cajones en la estrategia anterior, cada prisionero sigue un ciclo único que siempre termina con su propio número. En el caso de ocho prisioneros, esta estrategia de seguimiento del ciclo tiene éxito sí y solo sí la duración del ciclo más largo de la permutación es como máximo 4. Si una permutación contiene un ciclo de longitud 5 o más, todos los prisioneros cuyos números se encuentren en dicho ciclo no alcanzan su propio número después de cuatro pasos.

Probabilidad de éxito

Distribución de probabilidad de la duración del ciclo más largo de una permutación aleatoria de los números del 1 al 100. El área verde corresponde a la probabilidad de supervivencia de los prisioneros

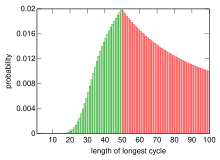
En el problema inicial, los 100 prisioneros tienen éxito si el ciclo más largo de la permutación tiene una longitud de 50 como máximo. Por lo tanto, su probabilidad de supervivencia es igual a la probabilidad de que una permutación aleatoria de los números del 1 al 100 no contenga ningún ciclo de longitud superior a 50. Esta probabilidad se determina a continuación.

Una permutación de los números del 1 al 100 puede contener como máximo un ciclo de longitud l > 50. Hay exactamente ${\tbinom {100}{l}}$ maneras de seleccionar los números de dicho ciclo (ver combinación). Dentro de este ciclo, estos números se pueden ordenar en (l-1)! ya que hay l permutaciones para representar distintos ciclos de longitud l debido a la simetría cíclica. Los números restantes se pueden organizar en (100-l)! maneras. Por lo tanto, el número de permutaciones de los números del 1 al 100 con un ciclo de longitud l > 50 es igual a

${\binom {100}{l}}\cdot (l-1)!\cdot (100-l)!={\frac {100!}{l}}.$

La probabilidad de que una permutación aleatoria (uniformemente distribuida) no contenga ningún ciclo de duración superior a 50 se calcula con la fórmula para eventos individuales y la fórmula para eventos complementarios así dada por

$1-{\frac {1}{100!}}\left({\frac {100!}{51}}+\ldots +{\frac {100!}{100}}\right)=1-\left({\frac {1}{51}}+\ldots +{\frac {1}{100}}\right)=1-(H_{100}-H_{50})\approx 0.31183,$

donde $H_{n}$ es el $n$-ésimo número armónico. Por lo tanto, utilizando la estrategia de seguimiento del ciclo, los prisioneros sobreviven en un sorprendente 31% de los casos.

Variantes

Problema de Monty Hall

En 2009, Adam S. Landsberg propuso la siguiente variante más simple del problema de los 100 prisioneros, que se basa en el conocido problema de Monty Hall.

Detrás de tres puertas cerradas, un coche, las llaves del coche y una cabra se distribuyen al azar. Hay dos jugadores: el primer jugador tiene que encontrar el coche, el segundo jugador las llaves del coche. Sólo si ambos jugadores tienen éxito pueden conducir el coche a casa. El primer jugador entra en la sala y puede abrir dos de las tres puertas consecutivamente. Si tiene éxito, las puertas se cierran de nuevo y el segundo jugador entra en la sala. El segundo jugador también puede abrir dos de las tres puertas, pero no puede comunicarse con el primer jugador de ninguna forma. ¿Cuál es la probabilidad de ganar si ambos jugadores actúan de forma óptima? ^{[cita requerida]}

Véase también

• Dilema del prisionero

• Datos: Q17265625