Arista (teoría de grafos)

En teoría de grafos, una arista o línea​ corresponde a una relación entre dos vértices de un grafo. En un grafo no dirigido, se trata de relaciones simétricas sin dirección, mientras que en un grafo dirigido son relaciones direccionales, también conocidas como arcos.​

Para caracterizar un grafo G son suficientes únicamente el conjunto de todas sus aristas, comúnmente denotado con la letra E (del término en inglés edge), junto con el conjunto de sus vértices, denotado por V. Así, dicho grafo se puede representar como G(V,E), o bien G = (V,E).

En un grafo, dos vértices son adyacentes si están conectados por una arista. En tal caso, cada uno de estos vértices es incidente a dicha arista.​

Representación

Representaciones gráficas de un grafo no dirigido, de un grafo dirigido, y de un grafo dirigido etiquetado.

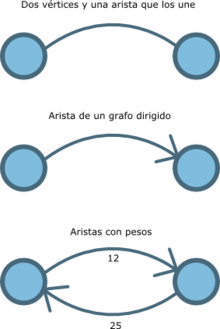
Gráficamente las aristas se representan, para el caso de los grafos no dirigidos, como una línea que une a los dos vértices. Si el grafo es dirigido, entonces la arista se representa como una flecha, que parte del nodo origen y apunta al nodo destino.

Algebraicamente, dado un grafo $G=(V,E)$ y dos vértices $a,b\in V$, una arista $e\in E$ se define, para un grafo no dirigido, como el conjunto $e=\{a,b\}=\{b,a\}$, en tanto que para un grafo dirigido, como el par ordenado $e=(a,b)=<a,b>$. Note que $(a,b)\neq (b,a)$.​

Por otro lado, también es normal que las aristas lleven asociadas una etiqueta (un número, una letra o un valor cualquiera) que indica una información asociada a ambos vértices, a veces un coste o indicación del trabajo necesario para recorrer el camino de un vértice al otro.

No es obligatorio que todo vértice esté unido con otro por una arista. Tales vértices se llaman vértices o nodos aislados.

Tampoco es necesario que ambos nodos unidos por una arista sean distintos. Dado un vértice a, de existir una arista {a, a} o bien (a, a), entonces se dice que el grafo posee un bucle.

Aplicaciones

En análisis de redes sociales, donde una red social se puede representar como un grafo, las aristas permiten construir díadas y se suelen interpretar como lazos interpersonales.​

Véase también

• Vértice
• Arista (geometría)

Bibliografía

• Diestel, Reinhard (1997), Graph Theory (en inglés), Springer-Verlag, Nueva York .
• Wasserman, Stanley; Faust, Katherine (2013) [1994]. Análisis de redes sociales: Métodos y aplicaciones. Madrid: Centro de Investigaciones Sociológicas. ISBN 978-84-7476-631-8. OCLC 871814053. 

• Datos: Q3297804