Plano de Laguerre

En matemáticas, un plano de Laguerre es uno de los tres tipos de Plano de Benz, que son el Plano de Möbius, el plano de Laguerre y el Minkowski plane. Los planos de Laguerre llevan el nombre del matemático French Edmond Laguerre.

classical Laguerre plane: 2d/3d-model

El plano de Laguerre clásico es un estructura de incidencia que describe el comportamiento de incidencia de las curvas $y=ax^{2}+bx+c$, es decir, parábolas y rectas, en el real affine plane. Para simplificar la estructura, a cualquier curva $y=ax^{2}+bx+c$ se le suma el punto $(\infty ,a)$. Una ventaja adicional de esta finalización es que la geometría plana de las parábolas/líneas completadas es isomorfismo con respecto a la geometría de las sección (geometría) de un cilindro (ver más abajo).

El plano de Laguerre real clásico

Originalmente, el plano de Laguerre clásico se definió como la geometría de las líneas y círculos orientados en el plano euclidiano real (ver​). Aquí preferimos el modelo de parábola del plano clásico de Laguerre.

Definimos:

${\mathcal {P}}:=\mathbb {R} ^{2}\cup (\{\infty \}\times \mathbb {R} ),\ \infty \notin \mathbb {R} ,$ el conjunto de puntos, ${\mathcal {Z}}:=\{\{(x,y)\in \mathbb {R} ^{2}\mid y=ax^{2}+bx+c\}\cup \{(\infty ,a)\}\mid a,b,c\in \mathbb {R} \}$ el conjunto de ciclos.

La estructura de incidencia $({\mathcal {P}},{\mathcal {Z}},\in )$ se denomina plano de Laguerre clásico.

El conjunto de puntos es $\mathbb {R} ^{2}$ más una copia de $\mathbb {R}$ (ver figura). Cualquier parábola/línea $y=ax^{2}+bx+c$ obtiene el punto adicional $(\infty ,a)$.

Los puntos con la misma coordenada x no pueden conectarse mediante curvas $y=ax^{2}+bx+c$. Por ello definimos:

Dos puntos $A,B$ son paralelos ($A\parallel B$) si $A=B$ o no hay ningún ciclo que contenga $A$ y $B$.

Para la descripción del plano real clásico de Laguerre sobre dos puntos $(a_{1},a_{2}),(b_{1},b_{2})$ son paralelos si y solo si $a_{1}=b_{1}$. $\parallel$ es un relación de equivalencia, similar a la paralelidad de líneas.

La estructura de incidencia $({\mathcal {P}},{\mathcal {Z}},\in )$ tiene las siguientes propiedades:

Lema:'

• Para tres puntos cualesquiera $A,B,C$, por pares y no paralelos, hay exactamente un ciclo $z$ que contiene $A,B,C$.
• Para cualquier punto $P$ y cualquier ciclo $z$ existe exactamente un punto $P'\in z$ tal que $P\parallel P'$.
• Para cualquier ciclo $z$, cualquier punto $P\in z$ y cualquier punto $Q\notin z$ que no sea paralelo a $P$ hay exactamente un ciclo $z'$ a $P,Q$ con $z\cap z'=\{P\}$, es decir, $z$ y $z'$ se tocan entre sí en $P$.

Laguerre-plane: stereographic projection of the x-z-plane onto a cylinder

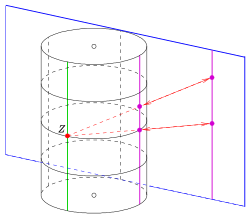
Similar al modelo de esfera del Plano de Möbius clásico, existe un modelo de cilindro para el plano de Laguerre clásico:

$({\mathcal {P}},{\mathcal {Z}},\in )$ es isomorfo a la geometría de secciones planas de un cilindro circular en $\mathbb {R} ^{3}$.

El siguiente mapeo $\Phi$ es una proyección con centro $(0,1,0)$ que mapea el plano x-z en el cilindro con la ecuación $u^{2}+v^{2}-v=0$, eje $(0,{\tfrac {1}{2}},..)$ y radio $r={\tfrac {1}{2}}\ :$.

$\Phi :\ (x,z)\rightarrow ({\frac {x}{1+x^{2}}},{\frac {x^{2}}{1+x^{2}}},{\frac {z}{1+x^{2}}})=(u,v,w)\ .$

• Los puntos $(0,1,a)$ (línea del cilindro que pasa por el centro) no aparecen como imágenes.
• $\Phi$ proyecta la parábola/recta con ecuación $z=ax^{2}+bx+c$ en el plano $w-a=bu+(a-c)(v-1)$. Entonces, la imagen de la parábola/línea es la sección plana del cilindro con un plano no perpendicular y por lo tanto un círculo/elipse sin punto $(0,1,a)$. Las parábolas/línea $z=ax^{2}+a$ se asignan a círculos (horizontales).
• Se asigna una línea (a=0) a un círculo/elipse que pasa por el centro $(0,1,0)$ y una parábola ($a\neq 0$) a un círculo/elipse que no contiene $(0,1,0)$.

Los axiomas de un plano de Laguerre

El Lema anterior da lugar a la siguiente definición:

Sea ${\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )$ una estructura de incidencia con el conjunto de puntos ${\mathcal {P}}$ y el conjunto de ciclos ${\mathcal {Z}}$.
Dos puntos $A,B$ son paralelos ($A\parallel B$) si $A=B$ o no hay ningún ciclo que contenga $A$ y $B$.
${\mathcal {L}}$ se denomina plano de Laguerre si se cumplen los siguientes axiomas:

Laguerre-plane: axioms

B1: Para tres puntos cualesquiera $A,B,C$, por pares y no paralelos, hay exactamente un ciclo $z$ que contiene $A,B,C$.

B2: Para cualquier punto $P$ y cualquier ciclo $z$ existe exactamente un punto $P'\in z$ tal que $P\parallel P'$.

B3: Para cualquier ciclo $z$, cualquier punto $P\in z$ y cualquier punto $Q\notin z$ que no sea paralelo a $P$ hay exactamente un ciclo $z'$ a $P,Q$ con $z\cap z'=\{P\}$,

es decir, $z$ y $z'$ se tocan entre sí en $P$.

B4: Cualquier ciclo contiene al menos tres puntos. Hay al menos un ciclo. Hay al menos cuatro puntos que no están en un ciclo.

Cuatro puntos $A,B,C,D$ son concíclicos si hay un ciclo $z$ con $A,B,C,D\in z$.

De la definición de la relación $\parallel$ y el axioma B2 obtenemos

Lema:' La relación $\parallel$ es una relación de equivalencia.

Siguiendo el modelo cilíndrico del plano de Laguerre clásico introducimos la denotación:

a) Para $P\in {\mathcal {P}}$ configuramos ${\overline {P}}:=\{Q\in {\mathcal {P}}\|\ P\parallel Q\}$. b) Una clase de equivalencia ${\overline {P}}$ se denomina generador.

Para el plano clásico de Laguerre, un generador es una línea paralela al eje y (modelo plano) o una línea en el cilindro (modelo espacial).

La conexión con la geometría lineal viene dada por la siguiente definición:

Para un plano de Laguerre ${\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )$ definimos la estructura local

${\mathcal {A}}_{P}:=({\mathcal {P}}\setminus \{{\overline {P}}\},\{z\setminus \{{\overline {P}}\}\|\ P\in z\in {\mathcal {Z}}\}\cup \{{\overline {Q}}\|\ Q\in {\mathcal {P}}\setminus \{{\overline {P}}\},\in )$

y llámelo residuo en el punto P.

En el modelo plano del plano clásico de Laguerre, ${\mathcal {A}}_{\infty }$ es el plano afín real $\mathbb {R} ^{2}$. En general obtenemos

Teorema: Cualquier residuo de un plano de Laguerre es un affine plane.

Y la definición equivalente de plano de Laguerre:

Teorema: Una estructura de incidencia junto con una relación de equivalencia $\parallel$ sobre ${\mathcal {P}}$ es una Plano de Laguerre si y solo si para cualquier punto $P$ el residuo ${\mathcal {A}}_{P}$ es un plano afín.

Planos finitos de Laguerre

minimal model of a Laguerre plane (only 4 of 8 cycles are shown)

La siguiente estructura de incidencia es un "modelo mínimo" de un plano de Laguerre:

${\mathcal {P}}:=\{A_{1},A_{2},B_{1},B_{2},C_{1},C_{2}\}\ ,$

${\mathcal {Z}}:=\{\{A_{i},B_{j},C_{k}\}\|\ i,j,k=1,2\}\ ,$

$A_{1}\parallel A_{2},\ B_{1}\parallel B_{2},\ C_{1}\parallel C_{2}\ .$

Por eso

$|{\mathcal {P}}|=6$ y $|{\mathcal {Z}}|=8\ .$

Para planos de Laguerre finitos, es decir $|{\mathcal {P}}|<\infty$, obtenemos:

Lema:' Para cualquier ciclo $z_{1},z_{2}$ y cualquier generador ${\overline {P}}$ de un plano de Laguerre finito ${\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )$ tenemos:

$|z_{1}|=|z_{2}|=|{\overline {P}}|+1$.

Para un plano de Laguerre finito ${\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )$ y un ciclo $z\in {\mathcal {Z}}$, el número entero $n:=|z|-1$ se denomina orden de ${\mathcal {L}}$.

De la combinatoria obtenemos

Lema:' Sea ${\mathcal {L}}:=({\mathcal {P}},{\mathcal {Z}},\in )$ un plano de orden de Laguerre $n$. Entonces

a) cualquier residuo ${\mathcal {A}}_{P}$ es un plano afín de orden $n\quad ,$ b) $|{\mathcal {P}}|=n^{2}+n,$ c) $|{\mathcal {Z}}|=n^{3}.$

Miquelian Laguerre aviones

A diferencia de los planos de Moebius, la generalización formal del modelo clásico de un plano de Laguerre, es decir, reemplazar $\mathbb {R}$ por un campo arbitrario $K$, siempre conduce a un ejemplo de plano de Laguerre.

Teorema: Para un field $K$ y

${\mathcal {P}}:=K^{2}\cup$ $(\{\infty \}\times K),\ \infty \notin K$,

${\mathcal {Z}}:=\{\{(x,y)\in K^{2}\|\ y=ax^{2}+bx+c\}\cup \{(\infty ,a)\}\|\ a,b,c\in K\}$ la estructura de incidencia

${\mathcal {L}}(K):=({\mathcal {P}},{\mathcal {Z}},\in )$ es un plano de Laguerre con la siguiente relación paralela: $(a_{1},a_{2})\parallel (b_{1},b_{2})$ si y solo si $a_{1}=b_{1}$.

De manera similar a un plano de Möbius, la versión de Laguerre del Teorema de Miquel sostiene:

Theorem of Miquel (circles drawn instead of parabolas)

Teorema de Miquel: Para el plano de Laguerre ${\mathcal {L}}(K)$ se cumple lo siguiente:

Si para 8 puntos $P_{1},\ldots ,P_{8}$ no paralelos en pares se pueden asignar a los vértices de un cubo de modo que los puntos en 5 caras correspondan a cuádruples concíclicos, entonces el sexto cuádruple de puntos también es concíclico.

(Para una mejor visión general en la figura hay círculos dibujados en lugar de parábolas)

La importancia del Teorema de Miquel se demuestra en el siguiente teorema, que se debe a v. d. Waerden, Smid y Chen:

Teorema: solo un plano de Laguerre ${\mathcal {L}}(K)$ satisface el teorema de Miquel.

Debido al último teorema, ${\mathcal {L}}(K)$ se denomina "plano de Miquelian Laguerre".

El modelo mínimo de un plano de Laguerre es miqueliano. Es isomorfo al plano de Laguerre ${\mathcal {L}}(K)$ con $K=GF(2)$ (campo $\{0,1\}$).

Un proyección estereográfica adecuado muestra que ${\mathcal {L}}(K)$ es isomorfo a la geometría de las secciones planas de un cilindro cuádrico sobre el campo $K$.

Planos ovoidales Laguerre

Hay muchos planos de Laguerre que no son miquelianos (ver enlace web más abajo). La clase que más se parece a los aviones miquelianos de Laguerre son los aviones ovoidales de Laguerre. Un plano ovoidal de Laguerre es la geometría de las secciones planas de un cilindro que se construye utilizando una oval en lugar de una cónica no degenerada. Un óvalo es un quadratic set y tiene las mismas propiedades geométricas que una cónica no degenerada en un plano proyectivo: 1) una recta corta a un óvalo en cero, uno o dos puntos y 2) en cualquier punto hay una tangente única. Se puede construir un óvalo simple en el plano real pegando dos mitades adecuadas de elipses diferentes, de modo que el resultado no sea una cónica. Incluso en el caso finito existen óvalos (ver quadratic set).

Véase también

• Transformaciones de Laguerre

Enlaces externos

• Plano Benz en el Encyclopaedia of Mathematics
• Nota de conferencia Geometrías circulares planas, una introducción a los planos de Moebius, Laguerre y Minkowski, págs.67

• Datos: Q15825031