Diferencia entre revisiones de «Teselado de Ammann-Beenker»

Contenido eliminado Contenido añadido

En renglón

Revisión del 16:23 21 sep 2023

A portion of tiling by Ammann's aperiodic A5 set of tiles, decorated with finite, local matching rules which force infinite, global structure, that of Amman–Beenker tiling.

En geometría, un mosaico de Ammann-Beenker es un tiling no periódico que puede generarse mediante un conjunto aperiódico de prototile como lo hizo Robert Ammann en la década de 1970, o mediante el método de cortar y proyectar como lo hizo de forma independiente F. P. M. Beenker. Son uno de los cinco conjuntos de mosaicos descubiertos por Ammann y descritos en Mosaicos y patrones.^[1]

Los mosaicos de Ammann-Beenker tienen muchas propiedades similares a los Teselación de Penrose más famosos:

No son periódicos, lo que significa que carecen de simetría traslacional.
Su no periodicidad está implícita en su estructura jerárquica: los mosaicos son mosaicos de sustitución que surgen de reglas de sustitución para parches cada vez más grandes. Esta estructura de sustitución también implica que:
Cualquier región finita (parche) en un mosaico aparece infinitas veces en ese mosaico y, de hecho, en cualquier otro mosaico. Por lo tanto, todos los mosaicos infinitos se ven similares entre sí, si uno mira solo los parches finitos.
Son cuasicristalline: implementados como una estructura física, un mosaico de Ammann-Beenker producirá Ley de Bragg; el difractograma revela tanto la simetría óctuple subyacente como el orden de largo alcance. Este orden refleja el hecho de que las cosas están organizadas, no a través de simetría traslacional, sino más bien a través de un proceso llamado a veces "deflación" o "inflación".
Toda esta estructura global infinita se fuerza a través de reglas de coincidencia locales en un par de mosaicos, uno de los conjuntos de mosaicos aperiódicos más simples jamás encontrados, el conjunto A5 de Ammann.^[1]

Se han propuesto varios métodos para describir los mosaicos: reglas de emparejamiento, sustituciones, esquemas de corte y proyecto^[2] y revestimientos.^[3]^[4] En 1987 Wang, Chen y Kuo anunciaron el descubrimiento de un cuasicristal con simetría octogonal.^[5]

==Descripción de los azulejos==.

Amman's A and B pair of A5 tiles, decorated with matching rules; any tiling by these tilings is necessarily non-periodic, and the tiles are therefore aperiodic.

Ammann A5 substitution rules, used to prove that the A5 tiles can only form non-periodic hierarchical tilings and thus are aperiodic tiles.

Los mosaicos A y B de Amman en su par A5, un rombo de 45-135 grados y un triángulo de 45-45-90 grados, decorados con reglas coincidentes que permitían solo ciertos arreglos en cada región, forzando las estructuras no periódicas, jerárquicas y cuasiperiódicas. de cada uno del infinito número de teselaciones individuales de Ammann-Beenker.

Un conjunto alternativo de mosaicos, también descubierto por Ammann, y denominado "Ammann 4" en Grünbaum y Shephard,^[1], consta de dos piezas no convexas con bordes en ángulo recto. Uno consta de dos cuadrados superpuestos sobre un cuadrado más pequeño, mientras que el otro consta de un cuadrado grande unido a un cuadrado más pequeño. Los siguientes diagramas muestran las piezas y una parte de los mosaicos.

Esta es la regla de sustitución para el conjunto de mosaicos alternativo.

La relación entre los dos conjuntos de mosaicos.

Además de las flechas de borde en el conjunto de mosaicos habitual, las reglas de coincidencia para ambos conjuntos de mosaicos se pueden expresar dibujando piezas de flechas grandes en los vértices y exigiendo que se unan para formar flechas completas.

Katz^[6] ha estudiado los mosaicos adicionales permitidos al eliminar las restricciones de los vértices e imponer solo el requisito de que las flechas de los bordes coincidan. Dado que este requisito es preservado por las reglas de sustitución, cualquier nuevo mosaico tiene una secuencia infinita de copias "ampliadas" obtenidas mediante aplicaciones sucesivas de la regla de sustitución. Cada mosaico de la secuencia es indistinguible de un verdadero mosaico de Ammann-Beenker en una escala sucesivamente mayor. Dado que algunos de estos mosaicos son periódicos, se deduce que no se puede determinar ninguna decoración de los mosaicos que fuerce la aperiodicidad observando cualquier parche finito del mosaico. La orientación de las flechas de los vértices que fuerzan la aperiodicidad, entonces, solo puede deducirse de todo el mosaico infinito.

El mosaico tiene también una propiedad extrema: entre los mosaicos cuyos rombos se "alternan" (es decir, siempre que dos rombos son adyacentes o separados por una fila de cuadrados, aparecen en diferentes orientaciones), la proporción de cuadrados resulta ser mínimo en los mosaicos de Ammann-Beenker.^[7]

Características de la relación Pell y plata

Los mosaicos de Ammann-Beenker están estrechamente relacionados con número plateado ( $1+{\sqrt {2}}$ ) y Número de Pell.

el esquema substitution $R\to RrR;r\to R$ introduce la relación como factor de escala: su matriz es la matriz de sustitución de Pell, y la serie de palabras producidas por la sustitución tiene la propiedad de que el número de $r$ y $R$ son iguales a números de Pell sucesivos.
los vector, valor y espacio propios de la matriz de sustitución son $1+{\sqrt {2}}$ y $1-{\sqrt {2}}$ .
En el conjunto de mosaicos alternativo, los bordes largos tienen lados $1+{\sqrt {2}}$ veces más largos que los bordes cortos.
Un conjunto de gusanos Conway, formado por las diagonales corta y larga de los rombos, forma las cadenas anteriores, con r como la diagonal corta y R como la diagonal larga. Por lo tanto, los Ammann bars también forman cuadrículas ordenadas por Pell.^[8]

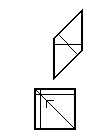Los Ammann bar para el conjunto de mosaicos habitual. Si se considera que las líneas exteriores en negrita tienen una longitud $2{\sqrt {2}}$ , las barras dividen los bordes en segmentos de longitud $1+{\sqrt {2}}$ y ${\sqrt {2}}-1$ . Estos mosaicos se denominan azulejos Ammann A5.

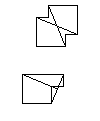Las barras de Ammann para el conjunto de mosaicos alternativo. Tenga en cuenta que las barras de la losa asimétrica se extienden parcialmente fuera de ella. Estos mosaicos se denominan azulejos Ammann A4.

Construcción de corte y proyecto

El tesseractic honeycomb tiene una simetría rotacional óctuple, correspondiente a una simetría rotacional óctuple del teseracto. Una matriz de rotación que representa esta simetría es:

A={\begin{bmatrix}0&0&0&-1\\1&0&0&0\\0&-1&0&0\\0&0&-1&0\end{bmatrix}}.

Transformando esta matriz a las nuevas coordenadas dadas por

B={\begin{bmatrix}-1/2&0&-1/2&{\sqrt {2}}/2\\1/2&{\sqrt {2}}/2&-1/2&0\\-1/2&0&-1/2&-{\sqrt {2}}/2\\-1/2&{\sqrt {2}}/2&1/2&0\end{bmatrix}}

producirá:

BAB^{-1}={\begin{bmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2&0&0\\-{\sqrt {2}}/2&{\sqrt {2}}/2&0&0\\0&0&-{\sqrt {2}}/2&{\sqrt {2}}/2\\0&0&-{\sqrt {2}}/2&-{\sqrt {2}}/2\end{bmatrix}}.

Esta tercera matriz corresponde entonces a una rotación tanto de 45° (en las dos primeras dimensiones) como de 135° (en las dos últimas). Luego podemos obtener un mosaico de Ammann-Beenker proyectando una losa de hipercubos en las dos primeras o las dos últimas de las nuevas coordenadas.

Alternativamente, se puede obtener un mosaico de Ammann-Beenker dibujando rombos y cuadrados alrededor de los puntos de intersección de un par de celosías cuadradas de igual escala superpuestas en un ángulo de 45 grados. Estas dos técnicas fueron desarrolladas por Beenker en su artículo.

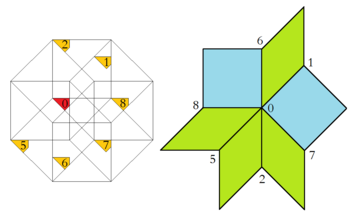
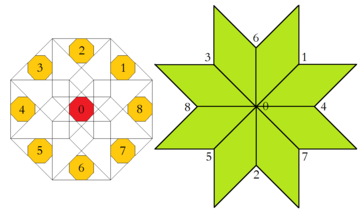
Una incrustación de alta dimensión relacionada en el tesseractic honeycomb es la construcción de Klotz, como se detalla en su aplicación aquí en el artículo de Baake y Joseph.^[9] Por lo tanto, el dominio de aceptación octogonal se puede dividir en partes, cada una de las cuales da lugar a exactamente una configuración de vértice. Además, el área relativa de cualquiera de estas regiones equivale a la frecuencia de la configuración de vértice correspondiente dentro del mosaico infinito.

Region of Acceptance Domain and Corresponding Vertex Configuration

Referencias y notas

↑ ^a ^b ^c Grünbaum, B.; Shephard, G. C. (1986). Tilings and Patterns. New York: Freeman. ISBN 0-7167-1193-1.
↑ Beenker FPM, Algebraic theory of non periodic tilings of the plane by two simple building blocks: a square and a rhombus, TH Report 82-WSK-04 (1982), Technische Hogeschool, Eindhoven
↑ F. Gähler, in Proceedings of the 6th International Conference on Quasicrystals, edited by S. Takeuchi and T. Fujiwara, World Scientific, Singapore, 1998, p. 95.
↑ Ben-Abraham, S. I.; Gähler, F. (1999). «Covering cluster description of octagonal MnSiAl quasicrystals». Physical Review B 60 (2): 860-864. doi:10.1103/PhysRevB.60.860. Archivado desde el original el June 17, 2007.
↑ Wang, N.; Chen, H.; Kuo, K. H. (1987). «Two-dimensional quasicrystal with eightfold rotational symmetry». Physical Review Letters 59 (9): 1010-1013. Bibcode:1987PhRvL..59.1010W. PMID 10035936. doi:10.1103/PhysRevLett.59.1010.
↑ Katz, A (1995). «Matching rules and quasiperiodicity: the octagonal tilings». En Axel, F.; Gratias, D., eds. Beyond quasicrystals. Springer. pp. 141-189. ISBN 978-3-540-59251-8. doi:10.1007/978-3-662-03130-8_6.
↑ Bédaride, N.; Fernique, T. (2013). «The Ammann-Beenker Tilings Revisited». En Schmid, S.; Withers, R.; Lifshitz, R., eds. Aperiodic Crystals. Springer. pp. 59-65. ISBN 978-94-007-6430-9. S2CID 8483564. arXiv:1208.3545v1. doi:10.1007/978-94-007-6431-6_8.
↑ Socolar, J E S (1989). «Simple octagonal and dodecagonal quasicrystals». Physical Review B 39 (15): 10519–10551. Bibcode:1989PhRvB..3910519S. PMID 9947860. doi:10.1103/PhysRevB.39.10519. MR0998533.
↑ Baake, M; Joseph, D (1990). «Ideal and Defective Vertex Configurations in the Planar Octagonal Quasilattice». Physical Review B 42 (13): 8091-8102. Bibcode:1990PhRvB..42.8091B. PMID 9994979. doi:10.1103/physrevb.42.8091.

Enlaces externos

Datos: Q4747168
Multimedia: Ammann–Beenker tiling / Q4747168

[ReferenceA-1] Grünbaum, B.; Shephard, G. C. (1986). Tilings and Patterns. New York: Freeman. ISBN 0-7167-1193-1.

[2] Beenker FPM, Algebraic theory of non periodic tilings of the plane by two simple building blocks: a square and a rhombus, TH Report 82-WSK-04 (1982), Technische Hogeschool, Eindhoven

[3] F. Gähler, in Proceedings of the 6th International Conference on Quasicrystals, edited by S. Takeuchi and T. Fujiwara, World Scientific, Singapore, 1998, p. 95.

[4] Ben-Abraham, S. I.; Gähler, F. (1999). «Covering cluster description of octagonal MnSiAl quasicrystals». Physical Review B 60 (2): 860-864. doi:10.1103/PhysRevB.60.860. Archivado desde el original el June 17, 2007.

[5] Wang, N.; Chen, H.; Kuo, K. H. (1987). «Two-dimensional quasicrystal with eightfold rotational symmetry». Physical Review Letters 59 (9): 1010-1013. Bibcode:1987PhRvL..59.1010W. PMID 10035936. doi:10.1103/PhysRevLett.59.1010.

[6] Katz, A (1995). «Matching rules and quasiperiodicity: the octagonal tilings». En Axel, F.; Gratias, D., eds. Beyond quasicrystals. Springer. pp. 141-189. ISBN 978-3-540-59251-8. doi:10.1007/978-3-662-03130-8_6.

[7] Bédaride, N.; Fernique, T. (2013). «The Ammann-Beenker Tilings Revisited». En Schmid, S.; Withers, R.; Lifshitz, R., eds. Aperiodic Crystals. Springer. pp. 59-65. ISBN 978-94-007-6430-9. S2CID 8483564. arXiv:1208.3545v1. doi:10.1007/978-94-007-6431-6_8.

[8] Socolar, J E S (1989). «Simple octagonal and dodecagonal quasicrystals». Physical Review B 39 (15): 10519–10551. Bibcode:1989PhRvB..3910519S. PMID 9947860. doi:10.1103/PhysRevB.39.10519. MR0998533.

[9] Baake, M; Joseph, D (1990). «Ideal and Defective Vertex Configurations in the Planar Octagonal Quasilattice». Physical Review B 42 (13): 8091-8102. Bibcode:1990PhRvB..42.8091B. PMID 9994979. doi:10.1103/physrevb.42.8091.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]