Diferencia entre revisiones de «Modelos compartimentales en epidemiología»
Traducido de en:Compartmental models in epidemiology Etiquetas: posible pruebas sin categorizar |
Traducido de en:Compartmental models in epidemiology exactamente de la versión https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology, bajo licencia GFDL y CC-BY-SA 3.0 |
||
| Línea 1: | Línea 1: | ||
Los modelos compartimentales constituyen una técnica utilizada para simplificar la modelización matemática de las enfermedades infecciosas.La población se divide en compartimentos, asumiendo que cada individuo en un mismo compartimento tiene las mismas características.Su origen se encuentra a principios del siglo XX, siendo un trabajo importante la primera investigación de Kermack y McKendrick en 1927. Los modelos suelen investigarse mediante ecuaciones diferenciales ordinarias (las cuales son determinísticas), pero también se pueden observar en un marco estocástico, el cual es más realista pero también más complicado de analizar.Los modelos compartimentales se pueden utilizar para predecir las características de propagación de una enfermedad, por ejemplo, la prevalencia (número total de infectados) o la duración de una [[epidemia]].Además, el modelo permite comprender cómo diferentes situaciones pueden afectar el resultado de la [[epidemia]], por ejemplo, cuál es la técnica más eficiente para emitir un número limitado de vacunas en una determinada población. |
Los modelos compartimentales constituyen una técnica utilizada para simplificar la modelización matemática de las enfermedades infecciosas.La población se divide en compartimentos, asumiendo que cada individuo en un mismo compartimento tiene las mismas características.Su origen se encuentra a principios del siglo XX, siendo un trabajo importante la primera investigación de Kermack y McKendrick en 1927. Los modelos suelen investigarse mediante ecuaciones diferenciales ordinarias (las cuales son determinísticas), pero también se pueden observar en un marco estocástico, el cual es más realista pero también más complicado de analizar.Los modelos compartimentales se pueden utilizar para predecir las características de propagación de una enfermedad, por ejemplo, la prevalencia (número total de infectados) o la duración de una [[epidemia]].Además, el modelo permite comprender cómo diferentes situaciones pueden afectar el resultado de la [[epidemia]], por ejemplo, cuál es la técnica más eficiente para emitir un número limitado de vacunas en una determinada población. |
||
== El modelo SIR == |
== El modelo SIR == |
||
El modelo SIR es uno de los modelos compartimentales más simples y muchos modelos derivan de este modelo básico.El modelo consta de tres compartimentos: S para el número de susceptibles, I para el número de infectados y R para el número de recuperados (o inmunes).Este modelo es razonablemente predictivo para enfermedades infecciosas que se transmiten de humano a humano y donde la recuperación confiere resistencia duradera, como el [[sarampión]], las paperas y la [[rubéola]]. |
El modelo SIR es uno de los modelos compartimentales más simples y muchos modelos derivan de este modelo básico.El modelo consta de tres compartimentos: S para el número de susceptibles, I para el número de infectados y R para el número de recuperados (o inmunes).Este modelo es razonablemente predictivo para enfermedades infecciosas que se transmiten de humano a humano y donde la recuperación confiere resistencia duradera, como el [[sarampión]], las paperas y la [[rubéola]]. |
||
Estas variables (S, I y R) representan el número de personas en cada compartimiento en un momento concreto.Para representar que el número de individuos susceptibles, infectados y recuperados puede variar con el tiempo (incluso si el tamaño de la población total permanece constante), los números precisos se convierten en una función de t (tiempo): S(t), I(t) y R(t).Para una enfermedad específica en una población específica, estas funciones pueden calcularse para predecir posibles brotes y controlarlos. |
Estas variables (S, I y R) representan el número de personas en cada compartimiento en un momento concreto.Para representar que el número de individuos susceptibles, infectados y recuperados puede variar con el tiempo (incluso si el tamaño de la población total permanece constante), los números precisos se convierten en una función de t (tiempo): S(t), I(t) y R(t).Para una enfermedad específica en una población específica, estas funciones pueden calcularse para predecir posibles brotes y controlarlos. |
||
=== El modelo SIR es dinámico en tres sentidos === |
=== El modelo SIR es dinámico en tres sentidos === |
||
En cuanto a la función variable de la t, el modelo es dinámico en tanto que los números en cada compartimento pueden fluctuar con el tiempo.La importancia de este aspecto dinámico es más evidente en una enfermedad endémica con un corto período infeccioso, como el [[sarampión]] en el Reino Unido antes de la introducción de la vacuna en 1968.Estas enfermedades tienden a ocurrir en ciclos de brotes debido a la variación en el número de casos susceptibles (S(t)) a lo largo del tiempo.Durante una [[epidemia]], el número de individuos susceptibles decrece rápidamente a medida que se infectan y, en consecuencia, entran en los compartimentos de infectados y recuperados.La enfermedad no puede brotar de nuevo hasta que el número de susceptibles haya vuelto a acumularse, por ejemplo, como resultado de la descendencia, que nace en el compartimento susceptible. |
En cuanto a la función variable de la t, el modelo es dinámico en tanto que los números en cada compartimento pueden fluctuar con el tiempo.La importancia de este aspecto dinámico es más evidente en una enfermedad endémica con un corto período infeccioso, como el [[sarampión]] en el Reino Unido antes de la introducción de la vacuna en 1968.Estas enfermedades tienden a ocurrir en ciclos de brotes debido a la variación en el número de casos susceptibles (S(t)) a lo largo del tiempo.Durante una [[epidemia]], el número de individuos susceptibles decrece rápidamente a medida que se infectan y, en consecuencia, entran en los compartimentos de infectados y recuperados.La enfermedad no puede brotar de nuevo hasta que el número de susceptibles haya vuelto a acumularse, por ejemplo, como resultado de la descendencia, que nace en el compartimento susceptible. |
||
Cada miembro de la población suele pasar de susceptible a infectado, y a recuperado.Esto se puede mostrar como un diagrama de flujo en el que los cuadros representan los diferentes compartimentos y las flechas la transición entre compartimentos, por ejemplo: |
Cada miembro de la población suele pasar de susceptible a infectado, y a recuperado.Esto se puede mostrar como un diagrama de flujo en el que los cuadros representan los diferentes compartimentos y las flechas la transición entre compartimentos, por ejemplo: |
||
=== Tasas de transición === |
=== Tasas de transición === |
||
Para que el modelo sea completamente específico, las flechas se tienen que etiquetar con las tasas de transición entre los compartimentos.Entre S y I, la tasa de transición es βI, donde β es el número promedio de contactos por persona por tiempo, multiplicado por la probabilidad de transmisión de la enfermedad en un contacto entre un sujeto susceptible y uno infectado.Entre I y R, la tasa de transición es γ (simplemente es la tasa de recuperación o muerte, es decir, el número de recuperados o muertos durante un día, dividido entre el número total de infectados de ese mismo día, suponiendo que el «día» es la unidad de tiempo).Si la duración de la infección es indicada como D, entonces γ = 1/D, ya que un individuo experimenta una recuperación en D unidades de tiempo.Se asume que la permanencia de cada sujeto en los estados epidémicos es una variable aleatoria con distribución exponencial.Se pueden utilizar distribuciones más complejas y realistas (como la distribución de Erlang) con algunas modificaciones. |
Para que el modelo sea completamente específico, las flechas se tienen que etiquetar con las tasas de transición entre los compartimentos.Entre S y I, la tasa de transición es βI, donde β es el número promedio de contactos por persona por tiempo, multiplicado por la probabilidad de transmisión de la enfermedad en un contacto entre un sujeto susceptible y uno infectado. Entre I y R, la tasa de transición es γ (simplemente es la tasa de recuperación o muerte, es decir, el número de recuperados o muertos durante un día, dividido entre el número total de infectados de ese mismo día, suponiendo que el «día» es la unidad de tiempo). Si la duración de la infección es indicada como D, entonces γ = 1/D, ya que un individuo experimenta una recuperación en D unidades de tiempo. Se asume que la permanencia de cada sujeto en los estados epidémicos es una variable aleatoria con distribución exponencial. Se pueden utilizar distribuciones más complejas y realistas (como la distribución de Erlang) con algunas modificaciones. |
||
== Tratamiento determinístico biomatemático del modelo SIR == |
== Tratamiento determinístico biomatemático del modelo SIR == |
||
=== El modelo SIR sin dinámica vital. === |
=== El modelo SIR sin dinámica vital. === |
||
La dinámica de una [[epidemia]], por ejemplo la [[gripe]], a menudo es mucho más rápida que la dinámica del nacimiento y la muerte, por lo tanto, el nacimiento y la muerte suelen omitirse en modelos compartimentales simples.El sistema SIR sin la denominada dinámica vital (nacimiento y muerte, a veces denominada demografía), descrito anteriormente, puede expresarse mediante el siguiente conjunto de ecuaciones diferenciales ordinarias: |
La dinámica de una [[epidemia]], por ejemplo la [[gripe]], a menudo es mucho más rápida que la dinámica del nacimiento y la muerte, por lo tanto, el nacimiento y la muerte suelen omitirse en modelos compartimentales simples. El sistema SIR sin la denominada dinámica vital (nacimiento y muerte, a veces denominada demografía), descrito anteriormente, puede expresarse mediante el siguiente conjunto de [[ecuaciones diferenciales]] ordinarias:<ref>{{cite journal |author=Hethcote H |title=The Mathematics of Infectious Diseases |journal=SIAM Review |volume=42 |issue= 4|pages=599–653 |year=2000 |doi=10.1137/s0036144500371907|bibcode=2000SIAMR..42..599H }}</ref> |
||
:<math> |
|||
\begin{align} |
|||
& \frac{dS}{dt} = - \frac{\beta I S}{N}, \\[6pt] |
|||
& \frac{dI}{dt} = \frac{\beta I S}{N}- \gamma I, \\[6pt] |
|||
& \frac{dR}{dt} = \gamma I, |
|||
\end{align} |
|||
</math> |
|||
donde <math>S</math> es el conjunto de la población susceptible, <math>I</math> es el conjunto de infectados, <math>R</math> el de la población sin la enfermedad (por muerte o recuperación) y <math>N</math> la suma de los tres. |
|||
Este modelo fue propuesto por primera vez por O. Kermack y Anderson Gray Mckendrick, como un caso especial de lo que ahora llamamos la teoría de Kermack y McKendrick, y dio seguimiento al trabajo de McKendrick con [[Ronald Ross]]. Este sistema es no lineal, sin embargo, es posible derivar su solución analítica de forma cerrada.<ref name="Harko">{{Cite journal|last=Harko|first=Tiberiu|last2=Lobo|first2=Francisco S. N.|last3=Mak|first3=M. K. |title=Exact analytical solutions of the Susceptible-Infected-Recovered (SIR) epidemic model and of the SIR model with equal death and birth rates |journal=Applied Mathematics and Computation|language=en|volume=236|pages=184–194|year=2014 |doi=10.1016/j.amc.2014.03.030|bibcode=2014arXiv1403.2160H |arxiv=1403.2160 }}</ref> Otras herramientas numéricas incluyen métodos de Monte Carlo, como el algoritmo Gillespie.Primero, nótese que: |
|||
:<math> \frac{dS}{dt} + \frac{dI}{dt} + \frac{dR}{dt} = 0,</math> |
|||
a lo que sigue: |
|||
:<math> S(t) + I(t) + R(t) = \text{constant} = N,</math> |
|||
expresando en términos matemáticos la constante de población <math> N </math>. Nótese que la relación anterior implica que tan solo se tiene que estudiar dos de las tres ecuaciones. |
|||
d |
|||
S |
|||
d |
|||
t |
|||
= |
|||
− |
|||
β |
|||
I |
|||
S |
|||
N |
|||
, |
|||
d |
|||
I |
|||
d |
|||
t |
|||
= |
|||
β |
|||
I |
|||
S |
|||
N |
|||
− |
|||
γ |
|||
I |
|||
, |
|||
d |
|||
R |
|||
d |
|||
t |
|||
= |
|||
γ |
|||
I |
|||
, |
|||
{\displaystyle {\begin{aligned}&{\frac {dS}{dt}}=-{\frac {\beta IS}{N}},\\[6pt]&{\frac {dI}{dt}}={\frac {\beta IS}{N}}-\gamma I,\\[6pt]&{\frac {dR}{dt}}=\gamma I,\end{aligned}}} |
|||
where |
|||
S |
|||
{\displaystyle S} |
|||
is the stock of susceptible population, |
|||
I |
|||
{\displaystyle I} |
|||
is the stock of infected, |
|||
R |
|||
{\displaystyle R} |
|||
is the stock of recovered population, and |
|||
N |
|||
{\displaystyle N} |
|||
is the sum of these three. |
|||
Este modelo fue propuesto por primera vez por O. Kermack y Anderson Gray Mckendrick, como un caso especial de lo que ahora llamamos la teoría de Kermack y McKendrick, y dio seguimiento al trabajo de McKendrick con [[Ronald Ross]].Este sistema es no lineal, sin embargo, es posible derivar su solución analítica de forma cerrada.Otras herramientas numéricas incluyen métodos de Monte Carlo, como el algoritmo Gillespie.Primero, nótese que: |
|||
d |
|||
S |
|||
d |
|||
t |
|||
+ |
|||
d |
|||
I |
|||
d |
|||
t |
|||
+ |
|||
d |
|||
R |
|||
d |
|||
t |
|||
= |
|||
0 |
|||
, |
|||
{\displaystyle {\frac {dS}{dt}}+{\frac {dI}{dt}}+{\frac {dR}{dt}}=0,} |
|||
it follows that: |
|||
S |
|||
( |
|||
t |
|||
) |
|||
+ |
|||
I |
|||
( |
|||
t |
|||
) |
|||
+ |
|||
R |
|||
( |
|||
t |
|||
) |
|||
= |
|||
constant |
|||
= |
|||
N |
|||
, |
|||
{\displaystyle S(t)+I(t)+R(t)={\text{constant}}=N,} |
|||
expressing in mathematical terms the constancy of population |
|||
N |
|||
{\displaystyle N} |
|||
. Note that the above relationship implies that one need only study the equation for two of the three variables. |
|||
En segundo lugar, observamos que la dinámica de la clase infecciosa depende de la siguiente relación: |
En segundo lugar, observamos que la dinámica de la clase infecciosa depende de la siguiente relación: |
||
:<math> R_0 = \frac{\beta}{\gamma},</math> |
|||
el llamado [[número básico reproductivo]] (también llamada ratio básica reproductiva). Esta ratio está derivada como el número de nuevas infecciones esperadas (estas nuevas infecciones se llaman secundarias) de una sola infección en una población donde todos los sujetos son susceptibles.<ref name="Bailey1975">{{cite book |author=Bailey, Norman T. J. |title=The mathematical theory of infectious diseases and its applications |publisher=Griffin |location=London |year=1975 |isbn=0-85264-231-8 |edition=2nd}}</ref><ref name="nunn2006">{{cite book |author1=Sonia Altizer |author2=Nunn, Charles |title=Infectious diseases in primates: behavior, ecology and evolution |publisher=Oxford University Press |location=Oxford [Oxfordshire] |year=2006 |isbn=0-19-856585-2 |series=Oxford Series in Ecology and Evolution}}</ref> Esta idea se puede comprobar mejor si se establece el tiempo típico entre contactos como <math>T_{c} = \beta^{-1}</math> y el tiempo típico hasta que no se tiene la enfermedad como <math>T_{r} = \gamma^{-1}</math>. Desde aquí sigue que, en general, el número de contactos con una persona infecciosa antes de que ya no tenga la enfermedad es: <math>T_{r}/T_{c}.</math> |
|||
R |
|||
0 |
|||
= |
|||
β |
|||
γ |
|||
, |
|||
{\displaystyle R_{0}={\frac {\beta }{\gamma }},} |
|||
the so-called basic reproduction number (also called basic reproduction ratio). This ratio is derived as the expected number of new infections (these new infections are sometimes called secondary infections) from a single infection in a population where all subjects are susceptible. This idea can probably be more readily seen if we say that the typical time between contacts is |
|||
T |
|||
c |
|||
= |
|||
β |
|||
− |
|||
1 |
|||
{\displaystyle T_{c}=\beta ^{-1}} |
|||
, and the typical time until recovery is |
|||
T |
|||
r |
|||
= |
|||
γ |
|||
− |
|||
1 |
|||
{\displaystyle T_{r}=\gamma ^{-1}} |
|||
. From here it follows that, on average, the number of contacts by an infected individual with others before the infected has recovered is: |
|||
T |
|||
r |
|||
/ |
|||
T |
|||
c |
|||
. |
|||
{\displaystyle T_{r}/T_{c}.} |
|||
Dividiendo la primera ecuación diferencial entre un tercio, separando las variables e integrando los datos obtenemos |
Dividiendo la primera ecuación diferencial entre un tercio, separando las variables e integrando los datos obtenemos |
||
:<math> S(t) = S(0) e^{-R_0(R(t) - R(0))/N}, </math> |
|||
donde <math>S(0)</math> y <math>R(0)</math> son los números iniciales de, respectivamente, susceptibles y sin enfermedad. Si escribimos <math>s_0 = S(0) / N</math> para la proporción inicial de susceptibles y <math>s_\infty = S(\infty) / N</math> and |
|||
<math>r_\infty = R(\infty) / N</math> para los susceptibles y sin enfermedad, respectivamente, en el límite <math>t \to \infty,</math> se obtiene |
|||
:<math>s_\infty = 1 - r_\infty = s_0 e^{-R_0(r_\infty - r_0)}</math> |
|||
(nótese que el compartimento de infecciosos se vacía en este límite). |
|||
S |
|||
( |
|||
t |
|||
) |
|||
= |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
Esta [[ecuación transcendental]] tiene una solución en términos de [[Lambert W function|Lambert {{mvar|W}} function]],<ref>{{cite web |author1=Wolfram Research, Inc. |title=Mathematica, Version 12.1 |url=https://www.wolfram.com/mathematica |publisher=Champaign IL, 2020}}</ref> que es: |
|||
e |
|||
:<math>s_\infty = 1-r_\infty = - R_0^{-1}\, W(-s_0 R_0 e^{-R_0(1-r_0)}).</math> |
|||
− |
|||
Esto muestra que al final de una epidemia, a no ser que <math>s_0=0</math>, no todos los individuos de una población no tienen la enfermedad, por lo tanto algunos pueden ser susceptibles. Esto quiere decir que el final de una epidemia está causada por el descenso en el número de infecciosos y no por la falta de sujetos susceptibles. |
|||
R |
|||
El rol del [[número básico reproductivo]] es extremadamente importante. De hecho, si reescribimos la ecuación para un individuo infeccioso de la siguiente manera: |
|||
0 |
|||
:<math> \frac{dI}{dt} = \left(R_0 \frac{S}{N} - 1\right) \gamma I,</math> |
|||
vemos que si: |
|||
( |
|||
R |
|||
( |
|||
t |
|||
) |
|||
− |
|||
R |
|||
( |
|||
0 |
|||
) |
|||
) |
|||
:<math> R_{0} > \frac{N}{S(0)},</math> |
|||
/ |
|||
entonces: |
|||
N |
|||
:<math> \frac{dI}{dt}(0) >0 ,</math> |
|||
habrá un brote epidémico con un número más alto de casos (lo que puede alcanzar a una gran parte de la población). Por el contrario: |
|||
, |
|||
:<math> R_{0} < \frac{N}{S(0)} ,</math> |
|||
entonces: |
|||
{\displaystyle S(t)=S(0)e^{-R_{0}(R(t)-R(0))/N},} |
|||
(where |
|||
:<math> \frac{dI}{dt}(0) <0 ,</math> |
|||
independientemente del tamaño inicial de la población susceptible, la enfermedad nunca puede causar un brote epidémico. Como consecuencia, está claro que el [[número básico reproductivo es muy importante. |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
{\displaystyle S(0)} |
|||
and |
|||
R |
|||
( |
|||
0 |
|||
) |
|||
{\displaystyle R(0)} |
|||
are the initial numbers of, respectively, susceptible and recovered subjects). Thus, in the limit |
|||
t |
|||
→ |
|||
+ |
|||
∞ |
|||
{\displaystyle t\to +\infty } |
|||
, the proportion of recovered individuals obeys the following transcendental equation |
|||
R |
|||
∞ |
|||
= |
|||
N |
|||
− |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
e |
|||
− |
|||
R |
|||
0 |
|||
( |
|||
R |
|||
∞ |
|||
− |
|||
R |
|||
( |
|||
0 |
|||
) |
|||
) |
|||
/ |
|||
N |
|||
. |
|||
{\displaystyle R_{\infty }=N-S(0)e^{-R_{0}(R_{\infty }-R(0))/N}.} |
|||
This equation shows that at the end of an epidemic, unless |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
= |
|||
0 |
|||
, |
|||
{\displaystyle S(0)=0,} |
|||
not all individuals of the population have recovered, so some must remain susceptible. This means that the end of an epidemic is caused by the decline in the number of infected individuals rather than an absolute lack of susceptible subjects. The role of the basic reproduction number is extremely important. In fact, upon rewriting the equation for infectious individuals as follows: |
|||
d |
|||
I |
|||
d |
|||
t |
|||
= |
|||
( |
|||
R |
|||
0 |
|||
S |
|||
N |
|||
− |
|||
1 |
|||
) |
|||
γ |
|||
I |
|||
, |
|||
{\displaystyle {\frac {dI}{dt}}=\left(R_{0}{\frac {S}{N}}-1\right)\gamma I,} |
|||
it yields that if: |
|||
R |
|||
0 |
|||
> |
|||
N |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
, |
|||
{\displaystyle R_{0}>{\frac {N}{S(0)}},} |
|||
then: |
|||
d |
|||
I |
|||
d |
|||
t |
|||
( |
|||
0 |
|||
) |
|||
> |
|||
0 |
|||
, |
|||
{\displaystyle {\frac {dI}{dt}}(0)>0,} |
|||
i.e., there will be a proper epidemic outbreak with an increase of the number of the infectious (which can reach a considerable fraction of the population). On the contrary, if |
|||
R |
|||
0 |
|||
< |
|||
N |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
, |
|||
{\displaystyle R_{0}<{\frac {N}{S(0)}},} |
|||
then |
|||
d |
|||
I |
|||
d |
|||
t |
|||
( |
|||
0 |
|||
) |
|||
< |
|||
0 |
|||
, |
|||
{\displaystyle {\frac {dI}{dt}}(0)<0,} |
|||
i.e., independently from the initial size of the susceptible population the disease can never cause a proper epidemic outbreak. As a consequence, it is clear that the basic reproduction number is extremely important. |
|||
=== La fuerza de la infección === |
=== La fuerza de la infección === |
||
Hay que tener en cuenta que en el modelo anterior la función: |
Hay que tener en cuenta que en el modelo anterior la función: |
||
:<math> F = \beta I,</math> |
|||
modela la ratio de transición del compartimento susceptible al infeccioso, así que se llama fuerza de la infección. Sin embargo, para clases de enfermedades más comunicables, es mas realista considerar la fuerza de la infección que no depende del número absoluto de infecciosos, pero de la fracción (con respecto a la constante total de población <math>N</math>): |
|||
:<math> F = \beta \frac{I}{N} .</math> |
|||
Capasso y, después, otros autores han propuesto fuerzas no-lineares para modelar de manera más realista el proceso de contagio. |
|||
F |
|||
= |
|||
β |
|||
I |
|||
, |
|||
{\displaystyle F=\beta I,} |
|||
models the transition rate from the compartment of susceptible individuals to the compartment of infectious individuals, so that it is called the force of infection. However, for large classes of communicable diseases it is more realistic to consider a force of infection that does not depend on the absolute number of infectious subjects, but on their fraction (with respect to the total constant population |
|||
N |
|||
{\displaystyle N} |
|||
): |
|||
F |
|||
= |
|||
β |
|||
I |
|||
N |
|||
. |
|||
{\displaystyle F=\beta {\frac {I}{N}}.} |
|||
Capasso and, afterwards, other authors have proposed nonlinear forces of infection to model more realistically the contagion process. |
|||
=== Soluciones analíticas exactas al modelo SIR === |
=== Soluciones analíticas exactas al modelo SIR === |
||
En el 2014, Harko y coautores derivaron una solución analítica exacta al modelo SIR.En el caso sin dinámica vital, para |
En el 2014, Harko y coautores derivaron una solución analítica exacta al modelo SIR. <ref name="Harko" /> En el caso sin dinámica vital, para <math>\mathcal{S}(u)=S(t)</math>, etc., corresponde a la siguiente parametización: |
||
:<math>\mathcal{S}(u)= S(0)u </math> |
|||
:<math>\mathcal{I}(u)= N -\mathcal{R}(u)-\mathcal{S}(u) </math> |
|||
:<math>\mathcal{R}(u)=R(0) -\rho \ln(u)</math> |
|||
para |
|||
:<math>t= \frac{N}{\beta}\int_u^1 \frac{du^*}{u^*\mathcal{I}(u^*)} , \quad \rho=\frac{\gamma N}{\beta},</math> |
|||
con condiciones iniciales |
|||
:<math>(\mathcal{S}(1),\mathcal{I}(1),\mathcal{R}(1))=(S(0),N -R(0)-S(0),R(0)), \quad u_T<u<1,</math> |
|||
S |
|||
donde <math>u_T</math> satisface <math>\mathcal{I}(u_T)=0</math>. Con la ecuación trascendental <math>R_{\infty}</math> anterior, sigue que <math>u_T=e^{-(R_{\infty}-R(0))/\rho}(=S_{\infty}/S(0)</math>, si <math>S(0) \neq 0)</math> y<math>I_{\infty}=0</math>. |
|||
Se encontró una solución analítica equivalente a los rendimientos de Miller<ref>{{cite journal | author = Miller, J.C. | title = A note on the derivation of epidemic final sizes | journal = Bulletin of Mathematical Biology | volume = 74 | issue = 9 | year=2012 | at= section 4.1| doi = 10.1007/s11538-012-9749-6 | pmid = 22829179 | pmc = 3506030 }}</ref><ref>{{cite journal | author = Miller, J.C. | title = Mathematical models of SIR disease spread with combined non-sexual and sexual transmission routes | journal = Infectious Disease Modelling | volume = 2 | issue = 1 | year=2017 | at = section 2.1.3| doi = 10.1016/j.idm.2016.12.003 | pmid = 29928728 | pmc = 5963332 }}</ref>: |
|||
( |
|||
u |
|||
) |
|||
= |
|||
S |
|||
( |
|||
t |
|||
) |
|||
:<math> |
|||
\begin{align} |
|||
S(t) & = S(0) e^{-\xi(t)} \\[8pt] |
|||
I(t) & = N-S(t)-R(t) \\[8pt] |
|||
R(t) & = R(0) + \rho \xi(t) \\[8pt] |
|||
\xi(t) & = \frac{\beta}{N}\int_0^t I(t^*) \, dt^* |
|||
\end{align} |
|||
</math> |
|||
Aquí <math>\xi(t)</math> se puede interpretar como el número esperado de transmisiones que un individuo ha recibido por tiempo <math>t</math>. Estas dos soluciones están relacionadas por <math>e^{-\xi(t)} = u</math |
|||
{\displaystyle {\mathcal {S}}(u)=S(t)} |
|||
, etc., it corresponds to the following time parametrization |
|||
Efectivamente, el mismo resultado puede encontrarse en el trabajo original de Kermack y Mckendrick. <ref name="Kermack–McKendrick" /> |
|||
Estas soluciones se entienden mejor si vemos que todos los términos en la parte de la derecha de las ecuaciones diferenciales son proporcionales a <math>I</math>. Las ecuaciones pueden ser divididas por <math>I</math>, y el tiempo reescalado para que el operador en la izquierda se convierta simplemente en <math>d/d\tau</math>, donde <math>d\tau=I dt</math>, por ejemplo <math>\tau=\int I dt</math>. Las ecuaciones diferenciales son ahora lineares y la tercera, con forma <math>dR/d\tau =</math> const., muestra que <math>\tau</math> y <math>R</math> (y arriba <math>\xi</math>) se crean simplemente lineares. |
|||
S |
|||
( |
|||
u |
|||
) |
|||
= |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
u |
|||
{\displaystyle {\mathcal {S}}(u)=S(0)u} |
|||
I |
|||
( |
|||
u |
|||
) |
|||
= |
|||
N |
|||
− |
|||
R |
|||
( |
|||
0 |
|||
) |
|||
+ |
|||
ρ |
|||
ln |
|||
|
|||
( |
|||
u |
|||
) |
|||
− |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
u |
|||
{\displaystyle {\mathcal {I}}(u)=N-R(0)+\rho \ln(u)-S(0)u} |
|||
R |
|||
( |
|||
u |
|||
) |
|||
= |
|||
R |
|||
( |
|||
0 |
|||
) |
|||
− |
|||
ρ |
|||
ln |
|||
|
|||
( |
|||
u |
|||
) |
|||
{\displaystyle {\mathcal {R}}(u)=R(0)-\rho \ln(u)} |
|||
for |
|||
t |
|||
= |
|||
∫ |
|||
u |
|||
1 |
|||
N |
|||
β |
|||
s |
|||
( |
|||
N |
|||
− |
|||
R |
|||
( |
|||
0 |
|||
) |
|||
+ |
|||
ρ |
|||
ln |
|||
|
|||
( |
|||
s |
|||
) |
|||
− |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
s |
|||
) |
|||
d |
|||
s |
|||
, |
|||
ρ |
|||
= |
|||
γ |
|||
N |
|||
β |
|||
, |
|||
{\displaystyle t=\int _{u}^{1}{\frac {N}{\beta s(N-R(0)+\rho \ln(s)-S(0)s)}}\,ds,\quad \rho ={\frac {\gamma N}{\beta }},} |
|||
with initial conditions |
|||
( |
|||
S |
|||
( |
|||
1 |
|||
) |
|||
, |
|||
I |
|||
( |
|||
1 |
|||
) |
|||
, |
|||
R |
|||
( |
|||
1 |
|||
) |
|||
) |
|||
= |
|||
( |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
, |
|||
N |
|||
− |
|||
R |
|||
( |
|||
0 |
|||
) |
|||
− |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
, |
|||
R |
|||
( |
|||
0 |
|||
) |
|||
) |
|||
, |
|||
u |
|||
T |
|||
< |
|||
u |
|||
< |
|||
1 |
|||
, |
|||
{\displaystyle ({\mathcal {S}}(1),{\mathcal {I}}(1),{\mathcal {R}}(1))=(S(0),N-R(0)-S(0),R(0)),\quad u_{T}<u<1,} |
|||
where |
|||
u |
|||
T |
|||
{\displaystyle u_{T}} |
|||
satisfies |
|||
I |
|||
( |
|||
u |
|||
T |
|||
) |
|||
= |
|||
0 |
|||
{\displaystyle {\mathcal {I}}(u_{T})=0} |
|||
. By the transcendental equation for |
|||
R |
|||
∞ |
|||
{\displaystyle R_{\infty }} |
|||
above, it follows that |
|||
u |
|||
T |
|||
= |
|||
e |
|||
− |
|||
( |
|||
R |
|||
∞ |
|||
− |
|||
R |
|||
( |
|||
0 |
|||
) |
|||
) |
|||
/ |
|||
ρ |
|||
( |
|||
= |
|||
S |
|||
∞ |
|||
/ |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
{\displaystyle u_{T}=e^{-(R_{\infty }-R(0))/\rho }(=S_{\infty }/S(0)} |
|||
, if |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
≠ |
|||
0 |
|||
) |
|||
{\displaystyle S(0)\neq 0)} |
|||
and |
|||
I |
|||
∞ |
|||
= |
|||
0 |
|||
{\displaystyle I_{\infty }=0} |
|||
. |
|||
Se encontró una solución analítica equivalente a los rendimientos de Miller |
|||
S |
|||
( |
|||
t |
|||
) |
|||
= |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
e |
|||
− |
|||
ξ |
|||
( |
|||
t |
|||
) |
|||
I |
|||
( |
|||
t |
|||
) |
|||
= |
|||
N |
|||
− |
|||
S |
|||
( |
|||
t |
|||
) |
|||
− |
|||
R |
|||
( |
|||
t |
|||
) |
|||
R |
|||
( |
|||
t |
|||
) |
|||
= |
|||
R |
|||
( |
|||
0 |
|||
) |
|||
+ |
|||
N |
|||
γ |
|||
β |
|||
ξ |
|||
( |
|||
t |
|||
) |
|||
ξ |
|||
( |
|||
t |
|||
) |
|||
= |
|||
β |
|||
∫ |
|||
0 |
|||
t |
|||
I |
|||
( |
|||
t |
|||
∗ |
|||
) |
|||
d |
|||
t |
|||
∗ |
|||
N |
|||
{\displaystyle {\begin{aligned}S(t)&=S(0)e^{-\xi (t)}\\[8pt]I(t)&=N-S(t)-R(t)\\[8pt]R(t)&=R(0)+N{\frac {\gamma }{\beta }}\xi (t)\\[8pt]\xi (t)&={\frac {\beta \int _{0}^{t}I(t^{*})\,dt^{*}}{N}}\end{aligned}}} |
|||
Here |
|||
ξ |
|||
( |
|||
t |
|||
) |
|||
{\displaystyle \xi (t)} |
|||
can be interpreted as the expected number of transmissions an individual has received by time |
|||
t |
|||
{\displaystyle t} |
|||
. The two solutions are related by |
|||
e |
|||
− |
|||
ξ |
|||
( |
|||
t |
|||
) |
|||
= |
|||
u |
|||
{\displaystyle e^{-\xi (t)}=u} |
|||
. |
|||
Efectivamente, el mismo resultado puede encontrarse en el trabajo original de Kermack y Mckendrick. |
|||
=== El modelo SIR con dinámica vital y población constante === |
=== El modelo SIR con dinámica vital y población constante === |
||
Considere una población caracterizada por una tasa de mortalidad |
Considere una población caracterizada por una tasa de mortalidad <math>\mu</math> y una ratio de nacimiento <math>\Lambda</math>, y donde enfermedades comunicables se propagan. El modelo de transmisión es: |
||
:<math> |
|||
\begin{align} |
|||
\frac{dS}{dt} & = \Lambda - \mu S - \frac{\beta I S}{N} \\[8pt] |
|||
\frac{dI}{dt} & = \frac{\beta I S}{N} - \gamma I -\mu I \\[8pt] |
|||
\frac{dR}{dt} & = \gamma I - \mu R |
|||
\end{align} |
|||
</math> |
|||
para el cual el equilibrio sin enfermedad (DFE, en inglés) es: |
|||
:<math>\left(S(t),I(t),R(t)\right) =\left(\frac{\Lambda}{\mu},0,0\right).</math> |
|||
μ |
|||
In this case, we can derive a [[basic reproduction number]]: |
|||
:<math> R_0 = \frac{ \beta\Lambda }{\mu(\mu+\gamma)}, </math> |
|||
{\displaystyle \mu } |
|||
and birth rate |
|||
which has threshold properties. In fact, independently from biologically meaningful initial values, one can show that: |
|||
:<math> R_0 \le 1 \Rightarrow \lim_{t \to \infty} (S(t),I(t),R(t)) = \textrm{DFE} = \left(\frac{\Lambda}{\mu},0,0\right) </math> |
|||
:<math> R_0 > 1 , I(0)> 0 \Rightarrow \lim_{t \to \infty} (S(t),I(t),R(t)) = \textrm{EE} = \left(\frac{\gamma+\mu}{\beta},\frac{\mu}{\beta}\left(R_0-1\right), \frac{\gamma}{\beta} \left(R_0-1\right)\right). </math> |
|||
The point EE is called the Endemic Equilibrium (the disease is not totally eradicated and remains in the population). With heuristic arguments, one may show that <math>R_{0}</math> may be read as the average number of infections caused by a single infectious subject in a wholly susceptible population, the above relationship biologically means that if this number is less than or equal to one the disease goes extinct, whereas if this number is greater than one the disease will remain permanently endemic in the population. |
|||
Λ |
|||
{\displaystyle \Lambda } |
|||
, and where a communicable disease is spreading. The model with mass-action transmission is: |
|||
d |
|||
S |
|||
d |
|||
t |
|||
= |
|||
Λ |
|||
− |
|||
μ |
|||
S |
|||
− |
|||
β |
|||
I |
|||
S |
|||
d |
|||
I |
|||
d |
|||
t |
|||
= |
|||
β |
|||
I |
|||
S |
|||
− |
|||
γ |
|||
I |
|||
− |
|||
μ |
|||
I |
|||
d |
|||
R |
|||
d |
|||
t |
|||
= |
|||
γ |
|||
I |
|||
− |
|||
μ |
|||
R |
|||
{\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\Lambda -\mu S-\beta IS\\[8pt]{\frac {dI}{dt}}&=\beta IS-\gamma I-\mu I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R\end{aligned}}} |
|||
for which the disease-free equilibrium (DFE) is: |
|||
( |
|||
S |
|||
( |
|||
t |
|||
) |
|||
, |
|||
I |
|||
( |
|||
t |
|||
) |
|||
, |
|||
R |
|||
( |
|||
t |
|||
) |
|||
) |
|||
= |
|||
( |
|||
Λ |
|||
μ |
|||
, |
|||
0 |
|||
, |
|||
0 |
|||
) |
|||
. |
|||
{\displaystyle \left(S(t),I(t),R(t)\right)=\left({\frac {\Lambda }{\mu }},0,0\right).} |
|||
In this case, we can derive a basic reproduction number: |
|||
R |
|||
0 |
|||
= |
|||
β |
|||
Λ |
|||
μ |
|||
( |
|||
μ |
|||
+ |
|||
γ |
|||
) |
|||
, |
|||
{\displaystyle R_{0}={\frac {\beta \Lambda }{\mu (\mu +\gamma )}},} |
|||
which has threshold properties. In fact, independently from biologically meaningful initial values, one can show that: |
|||
R |
|||
0 |
|||
≤ |
|||
1 |
|||
⇒ |
|||
lim |
|||
t |
|||
→ |
|||
∞ |
|||
( |
|||
S |
|||
( |
|||
t |
|||
) |
|||
, |
|||
I |
|||
( |
|||
t |
|||
) |
|||
, |
|||
R |
|||
( |
|||
t |
|||
) |
|||
) |
|||
= |
|||
DFE |
|||
= |
|||
( |
|||
Λ |
|||
μ |
|||
, |
|||
0 |
|||
, |
|||
0 |
|||
) |
|||
{\displaystyle R_{0}\leq 1\Rightarrow \lim _{t\to \infty }(S(t),I(t),R(t))={\textrm {DFE}}=\left({\frac {\Lambda }{\mu }},0,0\right)} |
|||
R |
|||
0 |
|||
> |
|||
1 |
|||
, |
|||
I |
|||
( |
|||
0 |
|||
) |
|||
> |
|||
0 |
|||
⇒ |
|||
lim |
|||
t |
|||
→ |
|||
∞ |
|||
( |
|||
S |
|||
( |
|||
t |
|||
) |
|||
, |
|||
I |
|||
( |
|||
t |
|||
) |
|||
, |
|||
R |
|||
( |
|||
t |
|||
) |
|||
) |
|||
= |
|||
EE |
|||
= |
|||
( |
|||
γ |
|||
+ |
|||
μ |
|||
β |
|||
, |
|||
μ |
|||
β |
|||
( |
|||
R |
|||
0 |
|||
− |
|||
1 |
|||
) |
|||
, |
|||
γ |
|||
β |
|||
( |
|||
R |
|||
0 |
|||
− |
|||
1 |
|||
) |
|||
) |
|||
. |
|||
{\displaystyle R_{0}>1,I(0)>0\Rightarrow \lim _{t\to \infty }(S(t),I(t),R(t))={\textrm {EE}}=\left({\frac {\gamma +\mu }{\beta }},{\frac {\mu }{\beta }}\left(R_{0}-1\right),{\frac {\gamma }{\beta }}\left(R_{0}-1\right)\right).} |
|||
The point EE is called the Endemic Equilibrium. With heuristic arguments, one may show that |
|||
R |
|||
0 |
|||
{\displaystyle R_{0}} |
|||
may be read as the average number of infections caused by a single infectious subject in a wholly susceptible population, the above relationship biologically means that if this number is less than or equal to one the disease goes extinct, whereas if this number is greater than one the disease will remain permanently endemic in the population. |
|||
== Modelo SIS == |
== Modelo SIS == |
||
[[File:SIS System Graph.svg|thumb|Yellow=Susceptible, Maroon=Infected]] |
|||
Algunas infecciones, por ejemplo las de la [[gripe]] común y la influenza, no confieren inmunidad duradera.Estas infecciones no dan inmunización al recuperarse de la infección, y los individuos vuelven a ser susceptibles. |
Algunas infecciones, por ejemplo las de la [[gripe]] común y la influenza, no confieren inmunidad duradera.Estas infecciones no dan inmunización al recuperarse de la infección, y los individuos vuelven a ser susceptibles. |
||
[[File:SIS compartment model.svg|400px|center|SIS compartmental model]] |
|||
Tenemos el modelo: |
Tenemos el modelo: |
||
:<math> |
|||
\begin{align} |
|||
\frac{dS}{dt} & = - \frac{\beta S I}{N} + \gamma I \\[6pt] |
|||
\frac{dI}{dt} & = \frac{\beta S I}{N} - \gamma I |
|||
\end{align} |
|||
</math> |
|||
Note that denoting with ''N'' the total population it holds that: |
|||
:<math>\frac{dS}{dt} + \frac{dI}{dt} = 0 \Rightarrow S(t)+I(t) = N</math>. |
|||
It follows that: |
|||
:<math> \frac{dI}{dt} = (\beta - \gamma) I - \frac{\beta}{N} I^2 </math>, |
|||
i.e. the dynamics of infectious is ruled by a [[logistic function]], so that <math>\forall I(0) > 0</math>: |
|||
:<math> |
|||
\begin{align} |
|||
& \frac{\beta}{\gamma} \le 1 \Rightarrow \lim_{t \to +\infty}I(t)=0, \\[6pt] |
|||
& \frac{\beta}{\gamma} > 1 \Rightarrow \lim_{t \to +\infty}I(t) = \left(1 - \frac{\gamma}{\beta} \right) N. |
|||
\end{align} |
|||
</math> |
|||
It is possible to find an analytical solution to this model (by making a transformation of variables: <math>I = y^{-1}</math> and substituting this into the mean-field equations),<ref name="Hethcote1989">{{cite book |last=Hethcote |first=Herbert W. |chapter=Three Basic Epidemiological Models |title=Applied Mathematical Ecology |editor1-last=Levin |editor1-first=Simon A. |editor2-last=Hallam |editor2-first=Thomas G. |editor3-last=Gross |editor3-first=Louis J. |series=Biomathematics |volume=18 |publisher=Springer |location=Berlin |year=1989 |pages=119–144 |isbn=3-540-19465-7 |doi=10.1007/978-3-642-61317-3_5 }}</ref> such that the basic reproduction rate is greater than unity. The solution is given as |
|||
:<math>I(t) = \frac{I_\infty}{1+V e^{-\chi t}}</math>. |
|||
where <math>I_\infty = (1 -\gamma/\beta)N</math> is the endemic infectious population, <math>\chi = \beta-\gamma</math>, and <math>V = I_\infty/I_0 - 1</math>. As the system is assumed to be closed, the susceptible population is then <math>S(t) = N - I(t)</math>. |
|||
As a special case, one obtains the usual logistic function by assuming <math>\gamma=0</math>. This can be also considered in the SIR model with <math>R=0</math>, i.e. no removal will take place. That is the ''SI model''.<ref>[http://math.colgate.edu/~wweckesser/math312Spring06/handouts/IMM_SI_Model.pdf (p. 19) The SI Model]</ref> The differential equation system using <math>S=N-I</math> thus reduces to: |
|||
d |
|||
S |
|||
:<math> |
|||
\frac{dI}{dt} \propto I\cdot (N-I). |
|||
</math> |
|||
In the long run, in this model, all individuals will become infected. |
|||
d |
|||
t |
|||
= |
|||
− |
|||
β |
|||
S |
|||
I |
|||
N |
|||
+ |
|||
γ |
|||
I |
|||
d |
|||
I |
|||
d |
|||
t |
|||
= |
|||
β |
|||
S |
|||
I |
|||
N |
|||
− |
|||
γ |
|||
I |
|||
{\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=-{\frac {\beta SI}{N}}+\gamma I\\[6pt]{\frac {dI}{dt}}&={\frac {\beta SI}{N}}-\gamma I\end{aligned}}} |
|||
Note that denoting with N the total population it holds that: |
|||
d |
|||
S |
|||
d |
|||
t |
|||
+ |
|||
d |
|||
I |
|||
d |
|||
t |
|||
= |
|||
0 |
|||
⇒ |
|||
S |
|||
( |
|||
t |
|||
) |
|||
+ |
|||
I |
|||
( |
|||
t |
|||
) |
|||
= |
|||
N |
|||
{\displaystyle {\frac {dS}{dt}}+{\frac {dI}{dt}}=0\Rightarrow S(t)+I(t)=N} |
|||
it follows that: |
|||
d |
|||
I |
|||
d |
|||
t |
|||
= |
|||
( |
|||
β |
|||
− |
|||
γ |
|||
) |
|||
I |
|||
− |
|||
β |
|||
N |
|||
I |
|||
2 |
|||
{\displaystyle {\frac {dI}{dt}}=(\beta -\gamma )I-{\frac {\beta }{N}}I^{2}} |
|||
i.e. the dynamics of infectious is ruled by a logistic equation, so that |
|||
∀ |
|||
I |
|||
( |
|||
0 |
|||
) |
|||
> |
|||
0 |
|||
{\displaystyle \forall I(0)>0} |
|||
: |
|||
β |
|||
γ |
|||
≤ |
|||
1 |
|||
⇒ |
|||
lim |
|||
t |
|||
→ |
|||
+ |
|||
∞ |
|||
I |
|||
( |
|||
t |
|||
) |
|||
= |
|||
0 |
|||
β |
|||
γ |
|||
> |
|||
1 |
|||
⇒ |
|||
lim |
|||
t |
|||
→ |
|||
+ |
|||
∞ |
|||
I |
|||
( |
|||
t |
|||
) |
|||
= |
|||
( |
|||
1 |
|||
− |
|||
γ |
|||
β |
|||
) |
|||
N |
|||
{\displaystyle {\begin{aligned}&{\frac {\beta }{\gamma }}\leq 1\Rightarrow \lim _{t\to +\infty }I(t)=0\\[6pt]&{\frac {\beta }{\gamma }}>1\Rightarrow \lim _{t\to +\infty }I(t)=\left(1-{\frac {\gamma }{\beta }}\right)N\end{aligned}}} |
|||
It is possible to find an analytical solution to this model (by making a transformation of variables: |
|||
I |
|||
= |
|||
y |
|||
− |
|||
1 |
|||
{\displaystyle I=y^{-1}} |
|||
and substituting this into the mean-field equations), such that the basic reproduction rate is greater than unity. The solution is given as |
|||
I |
|||
( |
|||
t |
|||
) |
|||
= |
|||
I |
|||
∞ |
|||
1 |
|||
+ |
|||
V |
|||
e |
|||
− |
|||
χ |
|||
t |
|||
{\displaystyle I(t)={\frac {I_{\infty }}{1+Ve^{-\chi t}}}} |
|||
where |
|||
I |
|||
∞ |
|||
= |
|||
( |
|||
1 |
|||
− |
|||
γ |
|||
/ |
|||
β |
|||
) |
|||
N |
|||
{\displaystyle I_{\infty }=(1-\gamma /\beta )N} |
|||
is the endemic infected population, |
|||
χ |
|||
= |
|||
β |
|||
− |
|||
γ |
|||
{\displaystyle \chi =\beta -\gamma } |
|||
, and |
|||
V |
|||
= |
|||
I |
|||
∞ |
|||
/ |
|||
I |
|||
0 |
|||
− |
|||
1 |
|||
{\displaystyle V=I_{\infty }/I_{0}-1} |
|||
. As the system is assumed to be closed, the susceptible population is then |
|||
S |
|||
( |
|||
t |
|||
) |
|||
= |
|||
N |
|||
− |
|||
I |
|||
( |
|||
t |
|||
) |
|||
{\displaystyle S(t)=N-I(t)} |
|||
. |
|||
== Explicaciones sobre el modelo SIR básico == |
== Explicaciones sobre el modelo SIR básico == |
||
| Línea 2007: | Línea 201: | ||
=== El modelo MSIR === |
=== El modelo MSIR === |
||
En muchas infecciones, incluyendo el [[sarampión]], los bebés no nacen en el compartimento susceptible, sino que son inmunes a la enfermedad durante los primeros meses de vida debido a la protección de los anticuerpos maternos (transmitidos a través de la [[placenta]] y adicionalmente a través del [[calostro]]).Esto se denomina inmunidad pasiva.Este detalle adicional puede demostrarse con una clase M (para la inmunidad maternal) al inicio del modelo |
En muchas infecciones, incluyendo el [[sarampión]], los bebés no nacen en el compartimento susceptible, sino que son inmunes a la enfermedad durante los primeros meses de vida debido a la protección de los anticuerpos maternos (transmitidos a través de la [[placenta]] y adicionalmente a través del [[calostro]]).Esto se denomina inmunidad pasiva.Este detalle adicional puede demostrarse con una clase M (para la inmunidad maternal) al inicio del modelo |
||
Para indicar esto matemáticamente, se añade un compartimento adicional, M(t), que tiene como resultado las siguientes ecuaciones diferenciales: |
Para indicar esto matemáticamente, se añade un compartimento adicional, M(t), que tiene como resultado las siguientes ecuaciones diferenciales: |
||
[[File:MSIR.PNG|800px|center|MSIR compartmental model]]To indicate this mathematically, an additional compartment is added, ''M''(''t'')''.'' This results in the following differential equations: |
|||
::<math> |
|||
\begin{align} |
|||
\frac{dM}{dT} & = \Lambda - \delta M - \mu M\\[8pt] |
|||
\frac{dS}{dT} & = \delta M - \frac{\beta SI}{N} - \mu S\\[8pt] |
|||
\frac{dI}{dT} & = \frac{\beta SI}{N} - \gamma I - \mu I\\[8pt] |
|||
\frac{dR}{dT} & = \gamma I - \mu R |
|||
\end{align} |
|||
</math> |
|||
d |
|||
M |
|||
d |
|||
T |
|||
= |
|||
B |
|||
− |
|||
δ |
|||
M |
|||
− |
|||
μ |
|||
M |
|||
d |
|||
S |
|||
d |
|||
T |
|||
= |
|||
δ |
|||
M |
|||
− |
|||
β |
|||
S |
|||
I |
|||
− |
|||
μ |
|||
S |
|||
d |
|||
I |
|||
d |
|||
T |
|||
= |
|||
β |
|||
S |
|||
I |
|||
− |
|||
γ |
|||
I |
|||
− |
|||
μ |
|||
I |
|||
d |
|||
R |
|||
d |
|||
T |
|||
= |
|||
γ |
|||
I |
|||
− |
|||
μ |
|||
R |
|||
{\displaystyle {\begin{aligned}{\frac {dM}{dT}}&=B-\delta M-\mu M\\[8pt]{\frac {dS}{dT}}&=\delta M-\beta SI-\mu S\\[8pt]{\frac {dI}{dT}}&=\beta SI-\gamma I-\mu I\\[8pt]{\frac {dR}{dT}}&=\gamma I-\mu R\end{aligned}}} |
|||
=== Estado de portador === |
=== Estado de portador === |
||
Algunas personas que han tenido una enfermedad infecciosa como la [[tuberculosis]] nunca se recuperan completamente y siguen llevando la infección, pese a que no sufren la enfermedad.Pueden volver a entrar al compartimento de infectados y sufrir síntomas (como en la [[tuberculosis]]) o pueden seguir infectando a otros en su estado de portador, a pesar de no padecer síntomas.El ejemplo más famoso de esto es, probablemente, Mary Mallon, que infectó a 22 personas con [[fiebre tifoidea]].El compartimento de portadores está marcado con C. |
Algunas personas que han tenido una enfermedad infecciosa como la [[tuberculosis]] nunca se recuperan completamente y siguen llevando la infección, pese a que no sufren la enfermedad.Pueden volver a entrar al compartimento de infectados y sufrir síntomas (como en la [[tuberculosis]]) o pueden seguir infectando a otros en su estado de portador, a pesar de no padecer síntomas.El ejemplo más famoso de esto es, probablemente, Mary Mallon, que infectó a 22 personas con [[fiebre tifoidea]].El compartimento de portadores está marcado con C. |
||
[[File:SIR with carrier model.png|A simple modification of previous image by Viki Male to make the word "Carrier" plainly visible.]] |
|||
=== Modelo SEIR === |
=== Modelo SEIR === |
||
Para muchas infecciones importantes existe un período de incubación significativo durante el cual los individuos han sido infectados, pero aún no son infecciosos por si mismos.Durante este periodo el individuo se encuentra en el compartimento E (de exposición). |
Para muchas infecciones importantes existe un período de incubación significativo durante el cual los individuos han sido infectados, pero aún no son infecciosos por si mismos.Durante este periodo el individuo se encuentra en el compartimento E (de exposición). |
||
[[File:SEIR.PNG|800px|center|SEIR compartmental model]] |
|||
Asumiendo que el período de incubación es una variable aleatoria con distribución exponencial con parámetro |
|||
Asumiendo que el período de incubación es una variable aleatoria con distribución exponencial con parámetro<math>a</math> (i.e. the average incubation period is <math>a^{-1}</math>), and also assuming the presence of vital dynamics with birth rate <math>\Lambda</math> equal to death rate <math>\mu</math>, we have the model: |
|||
:<math> |
|||
\begin{align} |
|||
\frac{dS}{dt} & = \mu N - \mu S - \beta \frac{I}{N} S \\[8pt] |
|||
\frac{dE}{dt} & = \beta \frac{I}{N} S - (\mu +a ) E \\[8pt] |
|||
\frac{dI}{dt} & = a E - (\gamma +\mu ) I \\[8pt] |
|||
\frac{dR}{dt} & = \gamma I - \mu R. |
|||
\end{align} |
|||
</math> |
|||
We have <math>S+E+I+R=N,</math> but this is only constant because of the (degenerate) assumption that birth and death rates are equal; in general <math>N</math> is a variable. |
|||
a |
|||
{\displaystyle a} |
|||
(i.e. the average incubation period is |
|||
a |
|||
− |
|||
1 |
|||
{\displaystyle a^{-1}} |
|||
), and also assuming the presence of vital dynamics with birth rate |
|||
Λ |
|||
{\displaystyle \Lambda } |
|||
equal to death rate |
|||
μ |
|||
{\displaystyle \mu } |
|||
, we have the model: |
|||
d |
|||
S |
|||
d |
|||
t |
|||
= |
|||
Λ |
|||
− |
|||
μ |
|||
S |
|||
− |
|||
β |
|||
I |
|||
N |
|||
S |
|||
d |
|||
E |
|||
d |
|||
t |
|||
= |
|||
β |
|||
I |
|||
N |
|||
S |
|||
− |
|||
( |
|||
μ |
|||
+ |
|||
a |
|||
) |
|||
E |
|||
d |
|||
I |
|||
d |
|||
t |
|||
= |
|||
a |
|||
E |
|||
− |
|||
( |
|||
γ |
|||
+ |
|||
μ |
|||
) |
|||
I |
|||
d |
|||
R |
|||
d |
|||
t |
|||
= |
|||
γ |
|||
I |
|||
− |
|||
μ |
|||
R |
|||
. |
|||
{\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\Lambda -\mu S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dE}{dt}}&=\beta {\frac {I}{N}}S-(\mu +a)E\\[8pt]{\frac {dI}{dt}}&=aE-(\gamma +\mu )I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R.\end{aligned}}} |
|||
We have |
|||
S |
|||
+ |
|||
E |
|||
+ |
|||
I |
|||
+ |
|||
R |
|||
= |
|||
N |
|||
, |
|||
{\displaystyle S+E+I+R=N,} |
|||
but this is only constant because of the (degenerate) assumption that birth and death rates are equal; in general |
|||
N |
|||
{\displaystyle N} |
|||
is a variable. |
|||
Para este modelo, el número de reproducción básico es: |
Para este modelo, el número de reproducción básico es: |
||
:<math>R_0 = \frac{a}{\mu+a}\frac{\beta}{\mu+\gamma}.</math> |
|||
Similarly to the SIR model, also, in this case, we have a Disease-Free-Equilibrium (''N'',0,0,0) and an Endemic Equilibrium EE, and one can show that, independently from biologically meaningful initial conditions |
|||
:<math> \left(S(0),E(0),I(0),R(0)\right) \in \left\{(S,E,I,R)\in [0,N]^4 : S \ge 0, E \ge 0, I\ge 0, R\ge 0, S+E+I+R = N \right\} </math> |
|||
it holds that: |
|||
:<math> R_0 \le 1 \Rightarrow \lim_{t \to +\infty} \left(S(t),E(t),I(t),R(t)\right) = DFE = (N,0,0,0),</math> |
|||
R |
|||
:<math> R_0 > 1 , I(0)> 0 \Rightarrow \lim_{t \to +\infty} \left(S(t),E(t),I(t),R(t)\right) = EE. </math> |
|||
0 |
|||
= |
|||
a |
|||
μ |
|||
+ |
|||
a |
|||
β |
|||
μ |
|||
+ |
|||
γ |
|||
. |
|||
{\displaystyle R_{0}={\frac {a}{\mu +a}}{\frac {\beta }{\mu +\gamma }}.} |
|||
Similarly to the SIR model, also in this case we have a Disease-Free-Equilibrium (N,0,0,0) and an Endemic Equilibrium EE, and one can show that, independently from biologically meaningful initial conditions |
|||
( |
|||
S |
|||
( |
|||
0 |
|||
) |
|||
, |
|||
E |
|||
( |
|||
0 |
|||
) |
|||
, |
|||
I |
|||
( |
|||
0 |
|||
) |
|||
, |
|||
R |
|||
( |
|||
0 |
|||
) |
|||
) |
|||
∈ |
|||
{ |
|||
( |
|||
S |
|||
, |
|||
E |
|||
, |
|||
I |
|||
, |
|||
R |
|||
) |
|||
∈ |
|||
[ |
|||
0 |
|||
, |
|||
N |
|||
] |
|||
4 |
|||
: |
|||
S |
|||
≥ |
|||
0 |
|||
, |
|||
E |
|||
≥ |
|||
0 |
|||
, |
|||
I |
|||
≥ |
|||
0 |
|||
, |
|||
R |
|||
≥ |
|||
0 |
|||
, |
|||
S |
|||
+ |
|||
E |
|||
+ |
|||
I |
|||
+ |
|||
R |
|||
= |
|||
N |
|||
} |
|||
{\displaystyle \left(S(0),E(0),I(0),R(0)\right)\in \left\{(S,E,I,R)\in [0,N]^{4}:S\geq 0,E\geq 0,I\geq 0,R\geq 0,S+E+I+R=N\right\}} |
|||
it holds that: |
|||
R |
|||
0 |
|||
≤ |
|||
1 |
|||
⇒ |
|||
lim |
|||
t |
|||
→ |
|||
+ |
|||
∞ |
|||
( |
|||
S |
|||
( |
|||
t |
|||
) |
|||
, |
|||
E |
|||
( |
|||
t |
|||
) |
|||
, |
|||
I |
|||
( |
|||
t |
|||
) |
|||
, |
|||
R |
|||
( |
|||
t |
|||
) |
|||
) |
|||
= |
|||
D |
|||
F |
|||
E |
|||
= |
|||
( |
|||
N |
|||
, |
|||
0 |
|||
, |
|||
0 |
|||
, |
|||
0 |
|||
) |
|||
, |
|||
{\displaystyle R_{0}\leq 1\Rightarrow \lim _{t\to +\infty }\left(S(t),E(t),I(t),R(t)\right)=DFE=(N,0,0,0),} |
|||
R |
|||
0 |
|||
> |
|||
1 |
|||
, |
|||
I |
|||
( |
|||
0 |
|||
) |
|||
> |
|||
0 |
|||
⇒ |
|||
lim |
|||
t |
|||
→ |
|||
+ |
|||
∞ |
|||
( |
|||
S |
|||
( |
|||
t |
|||
) |
|||
, |
|||
E |
|||
( |
|||
t |
|||
) |
|||
, |
|||
I |
|||
( |
|||
t |
|||
) |
|||
, |
|||
R |
|||
( |
|||
t |
|||
) |
|||
) |
|||
= |
|||
E |
|||
E |
|||
. |
|||
{\displaystyle R_{0}>1,I(0)>0\Rightarrow \lim _{t\to +\infty }\left(S(t),E(t),I(t),R(t)\right)=EE.} |
|||
In case of periodically varying contact rate |
|||
β |
|||
( |
|||
t |
|||
) |
|||
{\displaystyle \beta (t)} |
|||
the condition for the global attractiveness of DFE is that the following linear system with periodic coefficients: |
|||
d |
|||
E |
|||
1 |
|||
d |
|||
t |
|||
= |
|||
β |
|||
( |
|||
t |
|||
) |
|||
I |
|||
1 |
|||
− |
|||
( |
|||
γ |
|||
+ |
|||
a |
|||
) |
|||
E |
|||
1 |
|||
d |
|||
I |
|||
1 |
|||
d |
|||
t |
|||
= |
|||
a |
|||
E |
|||
1 |
|||
− |
|||
( |
|||
γ |
|||
+ |
|||
μ |
|||
) |
|||
I |
|||
1 |
|||
In case of periodically varying contact rate <math>\beta(t)</math> the condition for the global attractiveness of DFE is that the following linear system with periodic coefficients: |
|||
: <math> |
|||
\begin{align} |
|||
\frac{dE_1}{dt} & = \beta(t) I_1 - (\gamma +a ) E_1 \\[8pt] |
|||
\frac{dI_1}{dt} & = a E_1 - (\gamma +\mu ) I_1 |
|||
\end{align} |
|||
</math> |
|||
is stable (i.e. it has its Floquet's eigenvalues inside the unit circle in the complex plane). |
|||
{\displaystyle {\begin{aligned}{\frac {dE_{1}}{dt}}&=\beta (t)I_{1}-(\gamma +a)E_{1}\\[8pt]{\frac {dI_{1}}{dt}}&=aE_{1}-(\gamma +\mu )I_{1}\end{aligned}}} |
|||
is stable (i.e. it has its Floquet's eigenvalues inside the unit circle in the complex plane). |
|||
| Línea 2711: | Línea 269: | ||
:::<math>{\color{blue}{\mathcal{S} \to \mathcal{E} \to \mathcal{I} \to \mathcal{S}}}</math> |
|||
In this model an infection does not leave any immunity thus individuals that have recovered return to being susceptible, moving back into the ''S''(''t'') compartment. The following differential equations describe this model: |
|||
::<math> |
|||
\begin{align} |
|||
\frac{dS}{dT} & = \Lambda - \frac{\beta SI}{N} - \mu S + \gamma I \\[6pt] |
|||
\frac{dE}{dT} & = \frac{\beta SI}{N} - (\epsilon + \mu)E \\[6pt] |
|||
\frac{dI}{dT} & = \varepsilon E - (\gamma + \mu)I |
|||
\end{align} |
|||
S |
|||
</math> |
|||
→ |
|||
E |
|||
→ |
|||
I |
|||
→ |
|||
S |
|||
{\displaystyle {\color {blue}{{\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {S}}}}} |
|||
In this model an infection does not leave any immunity thus individuals that have recovered return to being susceptible again, moving back into the S(t) compartment. The following differential equations describe this model: |
|||
d |
|||
S |
|||
d |
|||
T |
|||
= |
|||
B |
|||
− |
|||
β |
|||
S |
|||
I |
|||
− |
|||
μ |
|||
S |
|||
+ |
|||
γ |
|||
I |
|||
d |
|||
E |
|||
d |
|||
T |
|||
= |
|||
β |
|||
S |
|||
I |
|||
− |
|||
( |
|||
ϵ |
|||
+ |
|||
μ |
|||
) |
|||
E |
|||
d |
|||
I |
|||
d |
|||
T |
|||
= |
|||
ε |
|||
E |
|||
− |
|||
( |
|||
γ |
|||
+ |
|||
μ |
|||
) |
|||
I |
|||
{\displaystyle {\begin{aligned}{\tfrac {dS}{dT}}&=B-\beta SI-\mu S+\gamma I\\[6pt]{\tfrac {dE}{dT}}&=\beta SI-(\epsilon +\mu )E\\[6pt]{\tfrac {dI}{dT}}&=\varepsilon E-(\gamma +\mu )I\end{aligned}}} |
|||
| Línea 2859: | Línea 286: | ||
En el caso de una enfermedad con los factores de inmunidad pasiva y un período de latencia, existe el modelo MSEIR. |
En el caso de una enfermedad con los factores de inmunidad pasiva y un período de latencia, existe el modelo MSEIR. |
||
:::<math> \color{blue}{\mathcal{M} \to \mathcal{S} \to \mathcal{E} \to \mathcal{I} \to \mathcal{R}} </math> |
|||
::<math> |
|||
\begin{align} |
|||
\frac{dM}{dT} & = \Lambda - \delta M - \mu M \\[6pt] |
|||
\frac{dS}{dT} & = \delta M - \frac{\beta SI}{N} - \mu S \\[6pt] |
|||
\frac{dE}{dT} & = \frac{\beta SI}{N} - (\varepsilon + \mu)E \\[6pt] |
|||
\frac{dI}{dT} & = \varepsilon E - (\gamma + \mu)I \\[6pt] |
|||
\frac{dR}{dT} & = \gamma I - \mu R |
|||
M |
|||
\end{align} |
|||
</math> |
|||
→ |
|||
S |
|||
→ |
|||
E |
|||
→ |
|||
I |
|||
→ |
|||
R |
|||
{\displaystyle \color {blue}{{\mathcal {M}}\to {\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {R}}}} |
|||
d |
|||
M |
|||
d |
|||
T |
|||
= |
|||
B |
|||
− |
|||
δ |
|||
M |
|||
− |
|||
μ |
|||
M |
|||
d |
|||
S |
|||
d |
|||
T |
|||
= |
|||
δ |
|||
M |
|||
− |
|||
β |
|||
S |
|||
I |
|||
− |
|||
μ |
|||
S |
|||
d |
|||
E |
|||
d |
|||
T |
|||
= |
|||
β |
|||
S |
|||
I |
|||
− |
|||
( |
|||
ε |
|||
+ |
|||
μ |
|||
) |
|||
E |
|||
d |
|||
I |
|||
d |
|||
T |
|||
= |
|||
ε |
|||
E |
|||
− |
|||
( |
|||
γ |
|||
+ |
|||
μ |
|||
) |
|||
I |
|||
d |
|||
R |
|||
d |
|||
T |
|||
= |
|||
γ |
|||
I |
|||
− |
|||
μ |
|||
R |
|||
{\displaystyle {\begin{aligned}{\tfrac {dM}{dT}}&=B-\delta M-\mu M\\[6pt]{\tfrac {dS}{dT}}&=\delta M-\beta SI-\mu S\\[6pt]{\tfrac {dE}{dT}}&=\beta SI-(\varepsilon +\mu )E\\[6pt]{\tfrac {dI}{dT}}&=\varepsilon E-(\gamma +\mu )I\\[6pt]{\tfrac {dR}{dT}}&=\gamma I-\mu R\end{aligned}}} |
|||
| Línea 3066: | Línea 301: | ||
Un modelo MSEIRS es similar al modelo MSEIR, pero la inmunidad en la clase R sería temporal, por lo que los individuos recuperarían su susceptibilidad cuando terminara la inmunidad temporal. |
Un modelo MSEIRS es similar al modelo MSEIR, pero la inmunidad en la clase R sería temporal, por lo que los individuos recuperarían su susceptibilidad cuando terminara la inmunidad temporal. |
||
:::<math>{\color{blue}{\mathcal{M} \to \mathcal{S} \to \mathcal{E} \to \mathcal{I} \to \mathcal{R} \to \mathcal{S}}}</math> |
|||
M |
|||
→ |
|||
S |
|||
→ |
|||
E |
|||
→ |
|||
I |
|||
→ |
|||
R |
|||
→ |
|||
S |
|||
{\displaystyle {\color {blue}{{\mathcal {M}}\to {\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {R}}\to {\mathcal {S}}}}} |
|||
=== Tasas de contacto variables y [[epidemia]]s plurianuales o caóticas. === |
=== Tasas de contacto variables y [[epidemia]]s plurianuales o caóticas. === |
||
Es bien sabido que la probabilidad de contraer una enfermedad no es constante en el tiempo.Algunas enfermedades son estacionales, tales como los virus del [[resfriado común]], que son más frecuentes durante el invierno.Con las enfermedades de la infancia, tales como el [[sarampión]], las paperas y la [[rubéola]], existe una fuerte correlación con el calendario escolar, por lo que durante las vacaciones escolares la probabilidad de contraer dicha enfermedad disminuye notablemente.Como consecuencia, para muchas clases de enfermedades se debe considerar una fuerza de infección con tasa de contacto periódica y variable ('estacional'). |
Es bien sabido que la probabilidad de contraer una enfermedad no es constante en el tiempo.Algunas enfermedades son estacionales, tales como los virus del [[resfriado común]], que son más frecuentes durante el invierno.Con las enfermedades de la infancia, tales como el [[sarampión]], las paperas y la [[rubéola]], existe una fuerte correlación con el calendario escolar, por lo que durante las vacaciones escolares la probabilidad de contraer dicha enfermedad disminuye notablemente.Como consecuencia, para muchas clases de enfermedades se debe considerar una fuerza de infección con tasa de contacto periódica y variable ('estacional'). |
||
s a consequence, for many classes of diseases, one should consider a force of infection with periodically ('seasonal') varying contact rate |
|||
:<math> F = \beta(t) \frac{I}{N} , \quad \beta(t+T)=\beta(t)</math> |
|||
with period T equal to one year. |
|||
F |
|||
= |
|||
β |
|||
( |
|||
t |
|||
) |
|||
I |
|||
N |
|||
, |
|||
β |
|||
( |
|||
t |
|||
+ |
|||
T |
|||
) |
|||
= |
|||
β |
|||
( |
|||
t |
|||
) |
|||
{\displaystyle F=\beta (t){\frac {I}{N}},\quad \beta (t+T)=\beta (t)} |
|||
with period T equal to one year. |
|||
Por lo tanto, nuestro modelo se convierte en |
Por lo tanto, nuestro modelo se convierte en |
||
\begin{align} |
|||
\frac{dS}{dt} & = \mu N - \mu S - \beta(t) \frac{I}{N} S \\[8pt] |
|||
\frac{dI}{dt} & = \beta(t) \frac{I}{N} S - (\gamma +\mu ) I |
|||
\end{align} |
|||
</math> |
|||
(the dynamics of recovered easily follows from <math>R=N-S-I</math>), i.e. a nonlinear set of differential equations with periodically varying parameters. It is well known that this class of dynamical systems may undergo very interesting and complex phenomena of nonlinear parametric resonance. It is easy to see that if: |
|||
:<math>\frac 1 T \int_0^T \frac{\beta(t)}{\mu+\gamma} \, dt < 1 \Rightarrow \lim_{t \to +\infty} (S(t),I(t)) = DFE = (N,0), </math> |
|||
whereas if the integral is greater than one the disease will not die out and there may be such resonances. For example, considering the periodically varying contact rate as the 'input' of the system one has that the output is a periodic function whose period is a multiple of the period of the input. |
|||
d |
|||
S |
|||
d |
|||
t |
|||
= |
|||
μ |
|||
N |
|||
− |
|||
μ |
|||
S |
|||
− |
|||
β |
|||
( |
|||
t |
|||
) |
|||
I |
|||
N |
|||
S |
|||
d |
|||
I |
|||
d |
|||
t |
|||
= |
|||
β |
|||
( |
|||
t |
|||
) |
|||
I |
|||
N |
|||
S |
|||
− |
|||
( |
|||
γ |
|||
+ |
|||
μ |
|||
) |
|||
I |
|||
{\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-\beta (t){\frac {I}{N}}S\\[8pt]{\frac {dI}{dt}}&=\beta (t){\frac {I}{N}}S-(\gamma +\mu )I\end{aligned}}} |
|||
(the dynamics of recovered easily follows from |
|||
R |
|||
= |
|||
N |
|||
− |
|||
S |
|||
− |
|||
I |
|||
{\displaystyle R=N-S-I} |
|||
), i.e. a nonlinear set of differential equations with periodically varying parameters. It is well known that this class of dynamical systems may undergo very interesting and complex phenomena of nonlinear parametric resonance. It is easy to see that if: |
|||
1 |
|||
T |
|||
∫ |
|||
0 |
|||
T |
|||
β |
|||
( |
|||
t |
|||
) |
|||
μ |
|||
+ |
|||
γ |
|||
d |
|||
t |
|||
< |
|||
1 |
|||
⇒ |
|||
lim |
|||
t |
|||
→ |
|||
+ |
|||
∞ |
|||
( |
|||
S |
|||
( |
|||
t |
|||
) |
|||
, |
|||
I |
|||
( |
|||
t |
|||
) |
|||
) |
|||
= |
|||
D |
|||
F |
|||
E |
|||
= |
|||
( |
|||
N |
|||
, |
|||
0 |
|||
) |
|||
, |
|||
{\displaystyle {\frac {1}{T}}\int _{0}^{T}{\frac {\beta (t)}{\mu +\gamma }}\,dt<1\Rightarrow \lim _{t\to +\infty }(S(t),I(t))=DFE=(N,0),} |
|||
whereas if the integral is greater than one the disease will not die out and there may be such resonances. For example, considering the periodically varying contact rate as the 'input' of the system one has that the output is a periodic function whose period is a multiple of the period of the input. |
|||
Esto permitió ayudar a explicar los brotes epidémicos polianuales (típicamente bienales) de algunas enfermedades infecciosas como interacción entre el período de las oscilaciones de la tasa de contacto y el seudo-período de las fluctuaciones que se encuentran cerca de la región endémica.Notablemente, el comportamiento también puede ser cuasi-periódico o incluso caótico. |
Esto permitió ayudar a explicar los brotes epidémicos polianuales (típicamente bienales) de algunas enfermedades infecciosas como interacción entre el período de las oscilaciones de la tasa de contacto y el seudo-período de las fluctuaciones que se encuentran cerca de la región endémica.Notablemente, el comportamiento también puede ser cuasi-periódico o incluso caótico. |
||
== Modelización de la vacunación == |
== Modelización de la vacunación == |
||
El modelo SIR se puede modificar para modelar la vacunación.Normalmente estos introducen un compartimento adicional al modelo SIR, |
El modelo SIR se puede modificar para modelar la vacunación.Normalmente estos introducen un compartimento adicional al modelo SIR, <math>V</math>, for vaccinated individuals.{{cn|date=September 2019}} Below are some examples. |
||
=== [[Vacunando]] recién nacidos === |
|||
V |
|||
En presencia de enfermedades transmisibles, una de las principales tareas es la erradicación mediante medidas de prevención y, si es posible, mediante el establecimiento de un programa de vacunación masiva.Considérese una enfermedad por la cual el recién nacido está vacunado (con una vacuna que administra inmunidad de por vida) a un ritmo <math>P \in (0,1)</math>: |
|||
:<math> |
|||
\begin{align} |
|||
\frac{dS}{dt} & = \mu N (1-P) - \mu S - \beta \frac{I}{N} S \\[8pt] |
|||
\frac{dI}{dt} & = \beta \frac{I}{N} S - (\mu+\gamma) I \\[8pt] |
|||
\frac{dV}{dt} & = \mu N P - \mu V |
|||
\end{align} |
|||
</math> |
|||
where <math>V</math> is the class of vaccinated subjects. It is immediate to show that: |
|||
{\displaystyle V} |
|||
, for vaccinated individuals. Below are some examples. |
|||
:<math> \lim_{t \to +\infty} V(t)= N P,</math> |
|||
thus we shall deal with the long term behavior of <math>S</math> and <math>I</math>, for which it holds that: |
|||
=== [[Vacuna]]ndo recién nacidos === |
|||
En presencia de enfermedades transmisibles, una de las principales tareas es la erradicación mediante medidas de prevención y, si es posible, mediante el establecimiento de un programa de vacunación masiva.Considérese una enfermedad por la cual el recién nacido está vacunado (con una vacuna que administra inmunidad de por vida) a un ritmo |
|||
:<math> R_0 (1-P) \le 1 \Rightarrow \lim_{t \to +\infty} \left(S(t),I(t)\right) = DFE = \left(N \left(1-P\right),0\right) </math> |
|||
:<math> R_0 (1-P) > 1 , \quad I(0)> 0 \Rightarrow \lim_{t \to +\infty} \left(S(t),I(t)\right) = EE = \left(\frac{N}{R_0(1-P)},N \left(R_0 (1-P)-1\right)\right). </math> |
|||
In other words, if |
|||
P |
|||
:<math> P < P^{*}= 1-\frac{1}{R_0} </math> |
|||
∈ |
|||
the vaccination program is not successful in eradicating the disease, on the contrary, it will remain endemic, although at lower levels than the case of absence of vaccinations. This means that the mathematical model suggests that for a disease whose [[basic reproduction number]] may be as high as 18 one should vaccinate at least 94.4% of newborns in order to eradicate the disease. |
|||
( |
|||
0 |
|||
, |
|||
1 |
|||
) |
|||
{\displaystyle P\in (0,1)} |
|||
: |
|||
d |
|||
S |
|||
d |
|||
t |
|||
= |
|||
μ |
|||
N |
|||
( |
|||
1 |
|||
− |
|||
P |
|||
) |
|||
− |
|||
μ |
|||
S |
|||
− |
|||
β |
|||
I |
|||
N |
|||
S |
|||
d |
|||
I |
|||
d |
|||
t |
|||
= |
|||
β |
|||
I |
|||
N |
|||
S |
|||
− |
|||
( |
|||
μ |
|||
+ |
|||
γ |
|||
) |
|||
I |
|||
d |
|||
V |
|||
d |
|||
t |
|||
= |
|||
μ |
|||
N |
|||
P |
|||
− |
|||
μ |
|||
V |
|||
{\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N(1-P)-\mu S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dI}{dt}}&=\beta {\frac {I}{N}}S-(\mu +\gamma )I\\[8pt]{\frac {dV}{dt}}&=\mu NP-\mu V\end{aligned}}} |
|||
where |
|||
V |
|||
{\displaystyle V} |
|||
is the class of vaccinated subjects. It is immediate to show that: |
|||
lim |
|||
t |
|||
→ |
|||
+ |
|||
∞ |
|||
V |
|||
( |
|||
t |
|||
) |
|||
= |
|||
N |
|||
P |
|||
, |
|||
{\displaystyle \lim _{t\to +\infty }V(t)=NP,} |
|||
thus we shall deal with the long term behavior of |
|||
S |
|||
{\displaystyle S} |
|||
and |
|||
I |
|||
{\displaystyle I} |
|||
, for which it holds that: |
|||
R |
|||
0 |
|||
( |
|||
1 |
|||
− |
|||
P |
|||
) |
|||
≤ |
|||
1 |
|||
⇒ |
|||
lim |
|||
t |
|||
→ |
|||
+ |
|||
∞ |
|||
( |
|||
S |
|||
( |
|||
t |
|||
) |
|||
, |
|||
I |
|||
( |
|||
t |
|||
) |
|||
) |
|||
= |
|||
D |
|||
F |
|||
E |
|||
= |
|||
( |
|||
N |
|||
( |
|||
1 |
|||
− |
|||
P |
|||
) |
|||
, |
|||
0 |
|||
) |
|||
{\displaystyle R_{0}(1-P)\leq 1\Rightarrow \lim _{t\to +\infty }\left(S(t),I(t)\right)=DFE=\left(N\left(1-P\right),0\right)} |
|||
R |
|||
0 |
|||
( |
|||
1 |
|||
− |
|||
P |
|||
) |
|||
> |
|||
1 |
|||
, |
|||
I |
|||
( |
|||
0 |
|||
) |
|||
> |
|||
0 |
|||
⇒ |
|||
lim |
|||
t |
|||
→ |
|||
+ |
|||
∞ |
|||
( |
|||
S |
|||
( |
|||
t |
|||
) |
|||
, |
|||
I |
|||
( |
|||
t |
|||
) |
|||
) |
|||
= |
|||
E |
|||
E |
|||
= |
|||
( |
|||
N |
|||
R |
|||
0 |
|||
( |
|||
1 |
|||
− |
|||
P |
|||
) |
|||
, |
|||
N |
|||
( |
|||
R |
|||
0 |
|||
( |
|||
1 |
|||
− |
|||
P |
|||
) |
|||
− |
|||
1 |
|||
) |
|||
) |
|||
. |
|||
{\displaystyle R_{0}(1-P)>1,\quad I(0)>0\Rightarrow \lim _{t\to +\infty }\left(S(t),I(t)\right)=EE=\left({\frac {N}{R_{0}(1-P)}},N\left(R_{0}(1-P)-1\right)\right).} |
|||
In other words, if |
|||
P |
|||
< |
|||
P |
|||
∗ |
|||
= |
|||
1 |
|||
− |
|||
1 |
|||
R |
|||
0 |
|||
{\displaystyle P<P^{*}=1-{\frac {1}{R_{0}}}} |
|||
the vaccination program is not successful in eradicating the disease, on the contrary it will remain endemic, although at lower levels than the case of absence of vaccinations. This means that the mathematical model suggests that for a disease whose basic reproduction number may be as high as 18 one should vaccinate at least 94.4% of newborns in order to eradicate the disease. |
|||
| Línea 3727: | Línea 363: | ||
Las sociedades modernas están enfrentándose al desafío de la exención “racional", es decir, la decisión de la familia de no vacunar a los niños como consecuencia de una comparación "racional" entre el riesgo percibido por la infección y los posibles daños por la vacuna.Para valorar si este comportamiento es realmente racional, es decir, si esto puede igualmente llevar a la erradicación de la enfermedad, simplemente hay que asumir que la tasa de vacunación es una función creciente del número de sujetos infecciosos: |
Las sociedades modernas están enfrentándose al desafío de la exención “racional", es decir, la decisión de la familia de no vacunar a los niños como consecuencia de una comparación "racional" entre el riesgo percibido por la infección y los posibles daños por la vacuna.Para valorar si este comportamiento es realmente racional, es decir, si esto puede igualmente llevar a la erradicación de la enfermedad, simplemente hay que asumir que la tasa de vacunación es una función creciente del número de sujetos infecciosos: |
||
:<math> P=P(I), \quad P'(I)>0.</math> |
|||
In such a case the eradication condition becomes: |
|||
:<math> P(0) \ge P^{*},</math> |
|||
i.e. the baseline vaccination rate should be greater than the "mandatory vaccination" threshold, which, in case of exemption, cannot hold. Thus, "rational" exemption might be myopic since it is based only on the current low incidence due to high vaccine coverage, instead taking into account future resurgence of infection due to coverage decline. |
|||
P |
|||
= |
|||
P |
|||
( |
|||
I |
|||
) |
|||
, |
|||
P |
|||
′ |
|||
( |
|||
I |
|||
) |
|||
> |
|||
0. |
|||
{\displaystyle P=P(I),\quad P'(I)>0.} |
|||
In such a case the eradication condition becomes: |
|||
P |
|||
( |
|||
0 |
|||
) |
|||
≥ |
|||
P |
|||
∗ |
|||
, |
|||
{\displaystyle P(0)\geq P^{*},} |
|||
i.e. the baseline vaccination rate should be greater than the "mandatory vaccination" threshold, which, in case of exemption, cannot hold. Thus, "rational" exemption might be myopic since it is based only on the current low incidence due to high vaccine coverage, instead taking into account future resurgence of infection due to coverage decline. |
|||
=== [[Vacuna]]ción de los no recién nacidos === |
=== [[Vacuna]]ción de los no recién nacidos === |
||
En el caso de que además haya vacunas a no recién nacidos a una tasa ρ, la ecuación para el sujeto susceptible y vacunado se debe modificar de la siguiente manera : |
En el caso de que además haya vacunas a no recién nacidos a una tasa ρ, la ecuación para el sujeto susceptible y vacunado se debe modificar de la siguiente manera : |
||
:<math> |
|||
\begin{align} |
|||
\frac{dS}{dt} & = \mu N (1-P) - \mu S - \rho S - \beta \frac{I}{N} S \\[8pt] |
|||
\frac{dV}{dt} & = \mu N P + \rho S - \mu V |
|||
\end{align} |
|||
</math> |
|||
leading to the following eradication condition: |
|||
:<math> P \ge 1- \left(1+\frac{\rho}{\mu}\right)\frac{1}{R_0} </math> |
|||
d |
|||
S |
|||
d |
|||
t |
|||
= |
|||
μ |
|||
N |
|||
( |
|||
1 |
|||
− |
|||
P |
|||
) |
|||
− |
|||
μ |
|||
S |
|||
− |
|||
ρ |
|||
S |
|||
− |
|||
β |
|||
I |
|||
N |
|||
S |
|||
d |
|||
V |
|||
d |
|||
t |
|||
= |
|||
μ |
|||
N |
|||
P |
|||
+ |
|||
ρ |
|||
S |
|||
− |
|||
μ |
|||
V |
|||
{\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N(1-P)-\mu S-\rho S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dV}{dt}}&=\mu NP+\rho S-\mu V\end{aligned}}} |
|||
leading to the following eradication condition: |
|||
P |
|||
≥ |
|||
1 |
|||
− |
|||
( |
|||
1 |
|||
+ |
|||
ρ |
|||
μ |
|||
) |
|||
1 |
|||
R |
|||
0 |
|||
{\displaystyle P\geq 1-\left(1+{\frac {\rho }{\mu }}\right){\frac {1}{R_{0}}}} |
|||
=== Estrategia de vacunación frecuente === |
=== Estrategia de vacunación frecuente === |
||
Esta estrategia vacuna repetidamente a un grupo de edad definido (como niños pequeños o ancianos) en una población susceptible a lo largo del tiempo. Con esta estrategia, se retira inmediatamente al grupo de individuos susceptibles, lo que permite la eliminación de una enfermedad infecciosa, (como el [[sarampión]]), de toda la población.Cada unidad de tiempo T, una fracción constante p de sujetos susceptibles se vacunan en un tiempo relativamente corto (respecto a la dinámica de la enfermedad).Esto lleva a las siguientes ecuaciones diferenciales impulsivas para los sujetos susceptibles y vacunados: |
Esta estrategia vacuna repetidamente a un grupo de edad definido (como niños pequeños o ancianos) en una población susceptible a lo largo del tiempo. Con esta estrategia, se retira inmediatamente al grupo de individuos susceptibles, lo que permite la eliminación de una enfermedad infecciosa, (como el [[sarampión]]), de toda la población.Cada unidad de tiempo T, una fracción constante p de sujetos susceptibles se vacunan en un tiempo relativamente corto (respecto a la dinámica de la enfermedad).Esto lleva a las siguientes ecuaciones diferenciales impulsivas para los sujetos susceptibles y vacunados: |
||
:<math> |
|||
\begin{align} |
|||
\frac{dS}{dt} & = \mu N - \mu S - \beta \frac{I}{N} S, \quad S(n T^+) = (1-p) S(n T^-), & & n=0,1,2,\ldots \\[8pt] |
|||
\frac{dV}{dt} & = - \mu V, \quad V(n T^+) = V(n T^-) + p S(n T^-), & & n=0,1,2,\ldots |
|||
\end{align} |
|||
</math> |
|||
It is easy to see that by setting {{math|1=''I'' = 0}} one obtains that the dynamics of the susceptible subjects is given by: |
|||
:<math> S^*(t) = 1- \frac{p}{1-(1-p)E^{-\mu T}} E^{-\mu MOD(t,T)} </math> |
|||
and that the eradication condition is: |
|||
:<math> R_0 \int_0^T S^*(t) \, dt < 1 </math> |
|||
d |
|||
S |
|||
d |
|||
t |
|||
= |
|||
μ |
|||
N |
|||
− |
|||
μ |
|||
S |
|||
− |
|||
β |
|||
I |
|||
N |
|||
S |
|||
, |
|||
S |
|||
( |
|||
n |
|||
T |
|||
+ |
|||
) |
|||
= |
|||
( |
|||
1 |
|||
− |
|||
p |
|||
) |
|||
S |
|||
( |
|||
n |
|||
T |
|||
− |
|||
) |
|||
, |
|||
n |
|||
= |
|||
0 |
|||
, |
|||
1 |
|||
, |
|||
2 |
|||
, |
|||
… |
|||
d |
|||
V |
|||
d |
|||
t |
|||
= |
|||
− |
|||
μ |
|||
V |
|||
, |
|||
V |
|||
( |
|||
n |
|||
T |
|||
+ |
|||
) |
|||
= |
|||
V |
|||
( |
|||
n |
|||
T |
|||
− |
|||
) |
|||
+ |
|||
p |
|||
S |
|||
( |
|||
n |
|||
T |
|||
− |
|||
) |
|||
, |
|||
n |
|||
= |
|||
0 |
|||
, |
|||
1 |
|||
, |
|||
2 |
|||
, |
|||
… |
|||
{\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-\beta {\frac {I}{N}}S,\quad S(nT^{+})=(1-p)S(nT^{-}),&&n=0,1,2,\ldots \\[8pt]{\frac {dV}{dt}}&=-\mu V,\quad V(nT^{+})=V(nT^{-})+pS(nT^{-}),&&n=0,1,2,\ldots \end{aligned}}} |
|||
It is easy to see that by setting I = 0 one obtains that the dynamics of the susceptible subjects is given by: |
|||
S |
|||
∗ |
|||
( |
|||
t |
|||
) |
|||
= |
|||
1 |
|||
− |
|||
p |
|||
1 |
|||
− |
|||
( |
|||
1 |
|||
− |
|||
p |
|||
) |
|||
E |
|||
− |
|||
μ |
|||
T |
|||
E |
|||
− |
|||
μ |
|||
M |
|||
O |
|||
D |
|||
( |
|||
t |
|||
, |
|||
T |
|||
) |
|||
{\displaystyle S^{*}(t)=1-{\frac {p}{1-(1-p)E^{-\mu T}}}E^{-\mu MOD(t,T)}} |
|||
and that the eradication condition is: |
|||
R |
|||
0 |
|||
∫ |
|||
0 |
|||
T |
|||
S |
|||
∗ |
|||
( |
|||
t |
|||
) |
|||
d |
|||
t |
|||
< |
|||
1 |
|||
{\displaystyle R_{0}\int _{0}^{T}S^{*}(t)\,dt<1} |
|||
== La influencia de la edad: modelos estructurados por edad == |
== La influencia de la edad: modelos estructurados por edad == |
||
La edad influye profundamente en la propagación de la enfermedad en una población, especialmente en la tasa de contacto.Esta tasa resume la efectividad de los contactos entre sujetos susceptibles e infecciosos.Teniendo en cuenta las edades de las clases epidémicas |
La edad influye profundamente en la propagación de la enfermedad en una población, especialmente en la tasa de contacto.Esta tasa resume la efectividad de los contactos entre sujetos susceptibles e infecciosos.Teniendo en cuenta las edades de las clases epidémicas <math>s(t,a),i(t,a),r(t,a)</math> (to limit ourselves to the susceptible-infectious-removed scheme) such that: |
||
:<math>S(t)=\int_0^{a_M} s(t,a)\,da </math> |
|||
:<math>I(t)=\int_0^{a_M} i(t,a)\,da</math> |
|||
:<math>R(t)=\int_0^{a_M} r(t,a)\,da</math> |
|||
s |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
, |
|||
i |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
, |
|||
r |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
(where <math>a_M \le +\infty</math> is the maximum admissible age) and their dynamics is not described, as one might think, by "simple" partial differential equations, but by [[integro-differential equation]]s: |
|||
:<math>\partial_t s(t,a) + \partial_a s(t,a) = -\mu(a) s(a,t) - s(a,t)\int_0^{a_M} k(a,a_1;t)i(a_1,t)\,da_1 </math> |
|||
{\displaystyle s(t,a),i(t,a),r(t,a)} |
|||
(to limit ourselves to the susceptible-infectious-removed scheme) such that: |
|||
:<math>\partial_t i(t,a) + \partial_a i(t,a) = s(a,t)\int_{0}^{a_M}{k(a,a_1;t)i(a_1,t)da_1} -\mu(a) i(a,t) - \gamma(a)i(a,t) </math> |
|||
:<math>\partial_t r(t,a) + \partial_a r(t,a) = -\mu(a) r(a,t) + \gamma(a)i(a,t) </math> |
|||
where: |
|||
:<math>F(a,t,i(\cdot,\cdot))=\int_0^{a_M} k(a,a_1;t)i(a_1,t) \, da_1 </math> |
|||
S |
|||
( |
|||
t |
|||
) |
|||
= |
|||
is the force of infection, which, of course, will depend, though the contact kernel <math> k(a,a_1;t) </math> on the interactions between the ages. |
|||
∫ |
|||
0 |
|||
a |
|||
M |
|||
s |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
d |
|||
a |
|||
{\displaystyle S(t)=\int _{0}^{a_{M}}s(t,a)\,da} |
|||
I |
|||
( |
|||
t |
|||
) |
|||
= |
|||
∫ |
|||
0 |
|||
a |
|||
M |
|||
i |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
d |
|||
a |
|||
{\displaystyle I(t)=\int _{0}^{a_{M}}i(t,a)\,da} |
|||
R |
|||
( |
|||
t |
|||
) |
|||
= |
|||
∫ |
|||
0 |
|||
a |
|||
M |
|||
r |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
d |
|||
a |
|||
{\displaystyle R(t)=\int _{0}^{a_{M}}r(t,a)\,da} |
|||
(where |
|||
a |
|||
M |
|||
≤ |
|||
+ |
|||
∞ |
|||
{\displaystyle a_{M}\leq +\infty } |
|||
is the maximum admissible age) and their dynamics is not described, as one might think, by "simple" partial differential equations, but by integro-differential equations: |
|||
∂ |
|||
t |
|||
s |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
+ |
|||
∂ |
|||
a |
|||
s |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
= |
|||
− |
|||
μ |
|||
( |
|||
a |
|||
) |
|||
s |
|||
( |
|||
a |
|||
, |
|||
t |
|||
) |
|||
− |
|||
s |
|||
( |
|||
a |
|||
, |
|||
t |
|||
) |
|||
∫ |
|||
0 |
|||
a |
|||
M |
|||
k |
|||
( |
|||
a |
|||
, |
|||
a |
|||
1 |
|||
; |
|||
t |
|||
) |
|||
i |
|||
( |
|||
a |
|||
1 |
|||
, |
|||
t |
|||
) |
|||
d |
|||
a |
|||
1 |
|||
{\displaystyle \partial _{t}s(t,a)+\partial _{a}s(t,a)=-\mu (a)s(a,t)-s(a,t)\int _{0}^{a_{M}}k(a,a_{1};t)i(a_{1},t)\,da_{1}} |
|||
∂ |
|||
t |
|||
i |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
+ |
|||
∂ |
|||
a |
|||
i |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
= |
|||
s |
|||
( |
|||
a |
|||
, |
|||
t |
|||
) |
|||
∫ |
|||
0 |
|||
a |
|||
M |
|||
k |
|||
( |
|||
a |
|||
, |
|||
a |
|||
1 |
|||
; |
|||
t |
|||
) |
|||
i |
|||
( |
|||
a |
|||
1 |
|||
, |
|||
t |
|||
) |
|||
d |
|||
a |
|||
1 |
|||
− |
|||
μ |
|||
( |
|||
a |
|||
) |
|||
i |
|||
( |
|||
a |
|||
, |
|||
t |
|||
) |
|||
− |
|||
γ |
|||
( |
|||
a |
|||
) |
|||
i |
|||
( |
|||
a |
|||
, |
|||
t |
|||
) |
|||
{\displaystyle \partial _{t}i(t,a)+\partial _{a}i(t,a)=s(a,t)\int _{0}^{a_{M}}{k(a,a_{1};t)i(a_{1},t)da_{1}}-\mu (a)i(a,t)-\gamma (a)i(a,t)} |
|||
∂ |
|||
t |
|||
r |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
+ |
|||
∂ |
|||
a |
|||
r |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
= |
|||
− |
|||
μ |
|||
( |
|||
a |
|||
) |
|||
r |
|||
( |
|||
a |
|||
, |
|||
t |
|||
) |
|||
+ |
|||
γ |
|||
( |
|||
a |
|||
) |
|||
i |
|||
( |
|||
a |
|||
, |
|||
t |
|||
) |
|||
{\displaystyle \partial _{t}r(t,a)+\partial _{a}r(t,a)=-\mu (a)r(a,t)+\gamma (a)i(a,t)} |
|||
where: |
|||
F |
|||
( |
|||
a |
|||
, |
|||
t |
|||
, |
|||
i |
|||
( |
|||
⋅ |
|||
, |
|||
⋅ |
|||
) |
|||
) |
|||
= |
|||
∫ |
|||
0 |
|||
a |
|||
M |
|||
k |
|||
( |
|||
a |
|||
, |
|||
a |
|||
1 |
|||
; |
|||
t |
|||
) |
|||
i |
|||
( |
|||
a |
|||
1 |
|||
, |
|||
t |
|||
) |
|||
d |
|||
a |
|||
1 |
|||
{\displaystyle F(a,t,i(\cdot ,\cdot ))=\int _{0}^{a_{M}}k(a,a_{1};t)i(a_{1},t)\,da_{1}} |
|||
is the force of infection, which, of course, will depend, though the contact kernel |
|||
k |
|||
( |
|||
a |
|||
, |
|||
a |
|||
1 |
|||
; |
|||
t |
|||
) |
|||
{\displaystyle k(a,a_{1};t)} |
|||
on the interactions between the ages. |
|||
La complejidad se agrega por las condiciones iniciales de los recién nacidos (es decir, por a=0), que son fáciles de infectar y eliminar: |
La complejidad se agrega por las condiciones iniciales de los recién nacidos (es decir, por a=0), que son fáciles de infectar y eliminar: |
||
:<math>i(t,0)=r(t,0)=0</math> |
|||
but that are nonlocal for the density of susceptible newborns: |
|||
:<math>s(t,0)= \int_0^{a_M} \left(\varphi_s(a) s(a,t)+\varphi_i(a) i(a,t)+\varphi_r(a) r(a,t)\right) \, da </math> |
|||
where <math>\varphi_j(a), j=s,i,r</math> are the fertilities of the adults. |
|||
i |
|||
( |
|||
t |
|||
, |
|||
0 |
|||
) |
|||
= |
|||
r |
|||
( |
|||
t |
|||
, |
|||
0 |
|||
) |
|||
= |
|||
0 |
|||
{\displaystyle i(t,0)=r(t,0)=0} |
|||
but that are nonlocal for the density of susceptible newborns: |
|||
s |
|||
( |
|||
t |
|||
, |
|||
0 |
|||
) |
|||
= |
|||
∫ |
|||
0 |
|||
a |
|||
M |
|||
( |
|||
φ |
|||
s |
|||
( |
|||
a |
|||
) |
|||
s |
|||
( |
|||
a |
|||
, |
|||
t |
|||
) |
|||
+ |
|||
φ |
|||
i |
|||
( |
|||
a |
|||
) |
|||
i |
|||
( |
|||
a |
|||
, |
|||
t |
|||
) |
|||
+ |
|||
φ |
|||
r |
|||
( |
|||
a |
|||
) |
|||
r |
|||
( |
|||
a |
|||
, |
|||
t |
|||
) |
|||
) |
|||
d |
|||
a |
|||
{\displaystyle s(t,0)=\int _{0}^{a_{M}}\left(\varphi _{s}(a)s(a,t)+\varphi _{i}(a)i(a,t)+\varphi _{r}(a)r(a,t)\right)\,da} |
|||
where |
|||
φ |
|||
j |
|||
( |
|||
a |
|||
) |
|||
, |
|||
j |
|||
= |
|||
s |
|||
, |
|||
i |
|||
, |
|||
r |
|||
{\displaystyle \varphi _{j}(a),j=s,i,r} |
|||
are the fertilities of the adults. |
|||
Además, definiendo ahora la densidad de la población total |
|||
n |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
= |
|||
s |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
+ |
|||
i |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
+ |
|||
r |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
{\displaystyle n(t,a)=s(t,a)+i(t,a)+r(t,a)} |
|||
one obtains: |
|||
∂ |
|||
t |
|||
n |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
+ |
|||
∂ |
|||
a |
|||
n |
|||
( |
|||
t |
|||
, |
|||
a |
|||
) |
|||
= |
|||
− |
|||
μ |
|||
( |
|||
a |
|||
) |
|||
n |
|||
( |
|||
a |
|||
, |
|||
t |
|||
) |
|||
{\displaystyle \partial _{t}n(t,a)+\partial _{a}n(t,a)=-\mu (a)n(a,t)} |
|||
In the simplest case of equal fertilities in the three epidemic classes, we have that in order to have demographic equilibrium the following necessary and sufficient condition linking the fertility |
|||
φ |
|||
( |
|||
. |
|||
) |
|||
{\displaystyle \varphi (.)} |
|||
with the mortality |
|||
μ |
|||
( |
|||
a |
|||
) |
|||
{\displaystyle \mu (a)} |
|||
must hold: |
|||
1 |
|||
= |
|||
∫ |
|||
0 |
|||
a |
|||
M |
|||
φ |
|||
( |
|||
a |
|||
) |
|||
exp |
|||
|
|||
( |
|||
− |
|||
∫ |
|||
0 |
|||
a |
|||
μ |
|||
( |
|||
q |
|||
) |
|||
d |
|||
q |
|||
) |
|||
d |
|||
a |
|||
{\displaystyle 1=\int _{0}^{a_{M}}\varphi (a)\exp \left(-\int _{0}^{a}{\mu (q)dq}\right)\,da} |
|||
and the demographic equilibrium is |
|||
n |
|||
∗ |
|||
( |
|||
a |
|||
) |
|||
= |
|||
C |
|||
exp |
|||
|
|||
( |
|||
− |
|||
∫ |
|||
0 |
|||
a |
|||
μ |
|||
( |
|||
q |
|||
) |
|||
d |
|||
q |
|||
) |
|||
, |
|||
{\displaystyle n^{*}(a)=C\exp \left(-\int _{0}^{a}\mu (q)\,dq\right),} |
|||
automatically ensuring the existence of the disease-free solution: |
|||
Además, definiendo ahora la densidad de la población total<math>n(t,a)=s(t,a)+i(t,a)+r(t,a)</math> one obtains: |
|||
:<math>\partial_t n(t,a) + \partial_a n(t,a) = -\mu(a) n(a,t) </math> |
|||
In the simplest case of equal fertilities in the three epidemic classes, we have that in order to have demographic equilibrium the following necessary and sufficient condition linking the fertility <math>\varphi(.)</math> with the mortality <math>\mu(a)</math> must hold: |
|||
:<math> 1 = \int_0^{a_M} \varphi(a) \exp\left(- \int_0^a{\mu(q)dq} \right) \, da </math> |
|||
D |
|||
F |
|||
S |
|||
( |
|||
a |
|||
) |
|||
= |
|||
( |
|||
and the demographic equilibrium is |
|||
n |
|||
:<math>n^*(a)=C \exp\left(- \int_0^a \mu(q) \, dq \right),</math> |
|||
∗ |
|||
automatically ensuring the existence of the disease-free solution: |
|||
:<math>DFS(a)= (n^*(a),0,0).</math> |
|||
( |
|||
a |
|||
) |
|||
, |
|||
0 |
|||
, |
|||
0 |
|||
) |
|||
. |
|||
A basic reproduction number can be calculated as the spectral radius of an appropriate functional operator. |
|||
{\displaystyle DFS(a)=(n^{*}(a),0,0).} |
|||
A basic reproduction number can be calculated as the spectral radius of an appropriate functional operator. |
|||
Revisión del 14:29 2 jun 2020
Los modelos compartimentales constituyen una técnica utilizada para simplificar la modelización matemática de las enfermedades infecciosas.La población se divide en compartimentos, asumiendo que cada individuo en un mismo compartimento tiene las mismas características.Su origen se encuentra a principios del siglo XX, siendo un trabajo importante la primera investigación de Kermack y McKendrick en 1927. Los modelos suelen investigarse mediante ecuaciones diferenciales ordinarias (las cuales son determinísticas), pero también se pueden observar en un marco estocástico, el cual es más realista pero también más complicado de analizar.Los modelos compartimentales se pueden utilizar para predecir las características de propagación de una enfermedad, por ejemplo, la prevalencia (número total de infectados) o la duración de una epidemia.Además, el modelo permite comprender cómo diferentes situaciones pueden afectar el resultado de la epidemia, por ejemplo, cuál es la técnica más eficiente para emitir un número limitado de vacunas en una determinada población.
El modelo SIR
El modelo SIR es uno de los modelos compartimentales más simples y muchos modelos derivan de este modelo básico.El modelo consta de tres compartimentos: S para el número de susceptibles, I para el número de infectados y R para el número de recuperados (o inmunes).Este modelo es razonablemente predictivo para enfermedades infecciosas que se transmiten de humano a humano y donde la recuperación confiere resistencia duradera, como el sarampión, las paperas y la rubéola.
Estas variables (S, I y R) representan el número de personas en cada compartimiento en un momento concreto.Para representar que el número de individuos susceptibles, infectados y recuperados puede variar con el tiempo (incluso si el tamaño de la población total permanece constante), los números precisos se convierten en una función de t (tiempo): S(t), I(t) y R(t).Para una enfermedad específica en una población específica, estas funciones pueden calcularse para predecir posibles brotes y controlarlos.
El modelo SIR es dinámico en tres sentidos
En cuanto a la función variable de la t, el modelo es dinámico en tanto que los números en cada compartimento pueden fluctuar con el tiempo.La importancia de este aspecto dinámico es más evidente en una enfermedad endémica con un corto período infeccioso, como el sarampión en el Reino Unido antes de la introducción de la vacuna en 1968.Estas enfermedades tienden a ocurrir en ciclos de brotes debido a la variación en el número de casos susceptibles (S(t)) a lo largo del tiempo.Durante una epidemia, el número de individuos susceptibles decrece rápidamente a medida que se infectan y, en consecuencia, entran en los compartimentos de infectados y recuperados.La enfermedad no puede brotar de nuevo hasta que el número de susceptibles haya vuelto a acumularse, por ejemplo, como resultado de la descendencia, que nace en el compartimento susceptible.
Cada miembro de la población suele pasar de susceptible a infectado, y a recuperado.Esto se puede mostrar como un diagrama de flujo en el que los cuadros representan los diferentes compartimentos y las flechas la transición entre compartimentos, por ejemplo:
Tasas de transición
Para que el modelo sea completamente específico, las flechas se tienen que etiquetar con las tasas de transición entre los compartimentos.Entre S y I, la tasa de transición es βI, donde β es el número promedio de contactos por persona por tiempo, multiplicado por la probabilidad de transmisión de la enfermedad en un contacto entre un sujeto susceptible y uno infectado. Entre I y R, la tasa de transición es γ (simplemente es la tasa de recuperación o muerte, es decir, el número de recuperados o muertos durante un día, dividido entre el número total de infectados de ese mismo día, suponiendo que el «día» es la unidad de tiempo). Si la duración de la infección es indicada como D, entonces γ = 1/D, ya que un individuo experimenta una recuperación en D unidades de tiempo. Se asume que la permanencia de cada sujeto en los estados epidémicos es una variable aleatoria con distribución exponencial. Se pueden utilizar distribuciones más complejas y realistas (como la distribución de Erlang) con algunas modificaciones.
Tratamiento determinístico biomatemático del modelo SIR
El modelo SIR sin dinámica vital.
La dinámica de una epidemia, por ejemplo la gripe, a menudo es mucho más rápida que la dinámica del nacimiento y la muerte, por lo tanto, el nacimiento y la muerte suelen omitirse en modelos compartimentales simples. El sistema SIR sin la denominada dinámica vital (nacimiento y muerte, a veces denominada demografía), descrito anteriormente, puede expresarse mediante el siguiente conjunto de ecuaciones diferenciales ordinarias:[1]
donde es el conjunto de la población susceptible, es el conjunto de infectados, el de la población sin la enfermedad (por muerte o recuperación) y la suma de los tres.
Este modelo fue propuesto por primera vez por O. Kermack y Anderson Gray Mckendrick, como un caso especial de lo que ahora llamamos la teoría de Kermack y McKendrick, y dio seguimiento al trabajo de McKendrick con Ronald Ross. Este sistema es no lineal, sin embargo, es posible derivar su solución analítica de forma cerrada.[2] Otras herramientas numéricas incluyen métodos de Monte Carlo, como el algoritmo Gillespie.Primero, nótese que:
a lo que sigue:
expresando en términos matemáticos la constante de población . Nótese que la relación anterior implica que tan solo se tiene que estudiar dos de las tres ecuaciones.
En segundo lugar, observamos que la dinámica de la clase infecciosa depende de la siguiente relación:
el llamado número básico reproductivo (también llamada ratio básica reproductiva). Esta ratio está derivada como el número de nuevas infecciones esperadas (estas nuevas infecciones se llaman secundarias) de una sola infección en una población donde todos los sujetos son susceptibles.[3][4] Esta idea se puede comprobar mejor si se establece el tiempo típico entre contactos como y el tiempo típico hasta que no se tiene la enfermedad como . Desde aquí sigue que, en general, el número de contactos con una persona infecciosa antes de que ya no tenga la enfermedad es:
Dividiendo la primera ecuación diferencial entre un tercio, separando las variables e integrando los datos obtenemos
donde y son los números iniciales de, respectivamente, susceptibles y sin enfermedad. Si escribimos para la proporción inicial de susceptibles y and para los susceptibles y sin enfermedad, respectivamente, en el límite se obtiene
(nótese que el compartimento de infecciosos se vacía en este límite).
Esta ecuación transcendental tiene una solución en términos de Lambert W function,[5] que es:
Esto muestra que al final de una epidemia, a no ser que , no todos los individuos de una población no tienen la enfermedad, por lo tanto algunos pueden ser susceptibles. Esto quiere decir que el final de una epidemia está causada por el descenso en el número de infecciosos y no por la falta de sujetos susceptibles.
El rol del número básico reproductivo es extremadamente importante. De hecho, si reescribimos la ecuación para un individuo infeccioso de la siguiente manera:
vemos que si:
entonces:
habrá un brote epidémico con un número más alto de casos (lo que puede alcanzar a una gran parte de la población). Por el contrario:
entonces:
independientemente del tamaño inicial de la población susceptible, la enfermedad nunca puede causar un brote epidémico. Como consecuencia, está claro que el [[número básico reproductivo es muy importante.
La fuerza de la infección
Hay que tener en cuenta que en el modelo anterior la función:
modela la ratio de transición del compartimento susceptible al infeccioso, así que se llama fuerza de la infección. Sin embargo, para clases de enfermedades más comunicables, es mas realista considerar la fuerza de la infección que no depende del número absoluto de infecciosos, pero de la fracción (con respecto a la constante total de población ):
Capasso y, después, otros autores han propuesto fuerzas no-lineares para modelar de manera más realista el proceso de contagio.
Soluciones analíticas exactas al modelo SIR
En el 2014, Harko y coautores derivaron una solución analítica exacta al modelo SIR. [2] En el caso sin dinámica vital, para , etc., corresponde a la siguiente parametización:
para
con condiciones iniciales
donde satisface . Con la ecuación trascendental anterior, sigue que , si y.
Se encontró una solución analítica equivalente a los rendimientos de Miller[6][7]:
Aquí se puede interpretar como el número esperado de transmisiones que un individuo ha recibido por tiempo . Estas dos soluciones están relacionadas por Error al representar (error de sintaxis): {\displaystyle e^{-\xi(t)} = u</math Efectivamente, el mismo resultado puede encontrarse en el trabajo original de Kermack y Mckendrick. <ref name="Kermack–McKendrick" /> Estas soluciones se entienden mejor si vemos que todos los términos en la parte de la derecha de las ecuaciones diferenciales son proporcionales a <math>I} . Las ecuaciones pueden ser divididas por , y el tiempo reescalado para que el operador en la izquierda se convierta simplemente en , donde , por ejemplo . Las ecuaciones diferenciales son ahora lineares y la tercera, con forma const., muestra que y (y arriba ) se crean simplemente lineares.
El modelo SIR con dinámica vital y población constante
Considere una población caracterizada por una tasa de mortalidad y una ratio de nacimiento , y donde enfermedades comunicables se propagan. El modelo de transmisión es:
para el cual el equilibrio sin enfermedad (DFE, en inglés) es:
In this case, we can derive a basic reproduction number:
which has threshold properties. In fact, independently from biologically meaningful initial values, one can show that:
The point EE is called the Endemic Equilibrium (the disease is not totally eradicated and remains in the population). With heuristic arguments, one may show that may be read as the average number of infections caused by a single infectious subject in a wholly susceptible population, the above relationship biologically means that if this number is less than or equal to one the disease goes extinct, whereas if this number is greater than one the disease will remain permanently endemic in the population.
Modelo SIS
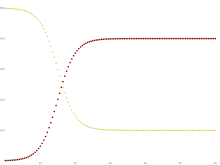
Algunas infecciones, por ejemplo las de la gripe común y la influenza, no confieren inmunidad duradera.Estas infecciones no dan inmunización al recuperarse de la infección, y los individuos vuelven a ser susceptibles.

Tenemos el modelo:
Note that denoting with N the total population it holds that:
- .
It follows that:
- ,
i.e. the dynamics of infectious is ruled by a logistic function, so that :
It is possible to find an analytical solution to this model (by making a transformation of variables: and substituting this into the mean-field equations),[8] such that the basic reproduction rate is greater than unity. The solution is given as
- .
where is the endemic infectious population, , and . As the system is assumed to be closed, the susceptible population is then .
As a special case, one obtains the usual logistic function by assuming . This can be also considered in the SIR model with , i.e. no removal will take place. That is the SI model.[9] The differential equation system using thus reduces to:
In the long run, in this model, all individuals will become infected.
Explicaciones sobre el modelo SIR básico
El modelo MSIR
En muchas infecciones, incluyendo el sarampión, los bebés no nacen en el compartimento susceptible, sino que son inmunes a la enfermedad durante los primeros meses de vida debido a la protección de los anticuerpos maternos (transmitidos a través de la placenta y adicionalmente a través del calostro).Esto se denomina inmunidad pasiva.Este detalle adicional puede demostrarse con una clase M (para la inmunidad maternal) al inicio del modelo
Para indicar esto matemáticamente, se añade un compartimento adicional, M(t), que tiene como resultado las siguientes ecuaciones diferenciales:

To indicate this mathematically, an additional compartment is added, M(t). This results in the following differential equations:
Estado de portador
Algunas personas que han tenido una enfermedad infecciosa como la tuberculosis nunca se recuperan completamente y siguen llevando la infección, pese a que no sufren la enfermedad.Pueden volver a entrar al compartimento de infectados y sufrir síntomas (como en la tuberculosis) o pueden seguir infectando a otros en su estado de portador, a pesar de no padecer síntomas.El ejemplo más famoso de esto es, probablemente, Mary Mallon, que infectó a 22 personas con fiebre tifoidea.El compartimento de portadores está marcado con C.
Modelo SEIR
Para muchas infecciones importantes existe un período de incubación significativo durante el cual los individuos han sido infectados, pero aún no son infecciosos por si mismos.Durante este periodo el individuo se encuentra en el compartimento E (de exposición).

Asumiendo que el período de incubación es una variable aleatoria con distribución exponencial con parámetro (i.e. the average incubation period is ), and also assuming the presence of vital dynamics with birth rate equal to death rate , we have the model:
We have but this is only constant because of the (degenerate) assumption that birth and death rates are equal; in general is a variable.
Para este modelo, el número de reproducción básico es:
Similarly to the SIR model, also, in this case, we have a Disease-Free-Equilibrium (N,0,0,0) and an Endemic Equilibrium EE, and one can show that, independently from biologically meaningful initial conditions
it holds that:
In case of periodically varying contact rate the condition for the global attractiveness of DFE is that the following linear system with periodic coefficients:
is stable (i.e. it has its Floquet's eigenvalues inside the unit circle in the complex plane).
Modelo SEIS
El modelo SEIS contempla el período de exposición, o periodo latente de la enfermedad, dando lugar a un compartimento adicional, E(t).
In this model an infection does not leave any immunity thus individuals that have recovered return to being susceptible, moving back into the S(t) compartment. The following differential equations describe this model:
Modelo MSEIR
En el caso de una enfermedad con los factores de inmunidad pasiva y un período de latencia, existe el modelo MSEIR.
Modelo MSEIRS.
Un modelo MSEIRS es similar al modelo MSEIR, pero la inmunidad en la clase R sería temporal, por lo que los individuos recuperarían su susceptibilidad cuando terminara la inmunidad temporal.
Tasas de contacto variables y epidemias plurianuales o caóticas.
Es bien sabido que la probabilidad de contraer una enfermedad no es constante en el tiempo.Algunas enfermedades son estacionales, tales como los virus del resfriado común, que son más frecuentes durante el invierno.Con las enfermedades de la infancia, tales como el sarampión, las paperas y la rubéola, existe una fuerte correlación con el calendario escolar, por lo que durante las vacaciones escolares la probabilidad de contraer dicha enfermedad disminuye notablemente.Como consecuencia, para muchas clases de enfermedades se debe considerar una fuerza de infección con tasa de contacto periódica y variable ('estacional').
s a consequence, for many classes of diseases, one should consider a force of infection with periodically ('seasonal') varying contact rate
with period T equal to one year.
Por lo tanto, nuestro modelo se convierte en
\begin{align} \frac{dS}{dt} & = \mu N - \mu S - \beta(t) \frac{I}{N} S \\[8pt] \frac{dI}{dt} & = \beta(t) \frac{I}{N} S - (\gamma +\mu ) I \end{align} </math>
(the dynamics of recovered easily follows from ), i.e. a nonlinear set of differential equations with periodically varying parameters. It is well known that this class of dynamical systems may undergo very interesting and complex phenomena of nonlinear parametric resonance. It is easy to see that if:
whereas if the integral is greater than one the disease will not die out and there may be such resonances. For example, considering the periodically varying contact rate as the 'input' of the system one has that the output is a periodic function whose period is a multiple of the period of the input.
Esto permitió ayudar a explicar los brotes epidémicos polianuales (típicamente bienales) de algunas enfermedades infecciosas como interacción entre el período de las oscilaciones de la tasa de contacto y el seudo-período de las fluctuaciones que se encuentran cerca de la región endémica.Notablemente, el comportamiento también puede ser cuasi-periódico o incluso caótico.
Modelización de la vacunación
El modelo SIR se puede modificar para modelar la vacunación.Normalmente estos introducen un compartimento adicional al modelo SIR, , for vaccinated individuals.[cita requerida] Below are some examples.
Vacunando recién nacidos
En presencia de enfermedades transmisibles, una de las principales tareas es la erradicación mediante medidas de prevención y, si es posible, mediante el establecimiento de un programa de vacunación masiva.Considérese una enfermedad por la cual el recién nacido está vacunado (con una vacuna que administra inmunidad de por vida) a un ritmo :
where is the class of vaccinated subjects. It is immediate to show that:
thus we shall deal with the long term behavior of and , for which it holds that:
In other words, if
the vaccination program is not successful in eradicating the disease, on the contrary, it will remain endemic, although at lower levels than the case of absence of vaccinations. This means that the mathematical model suggests that for a disease whose basic reproduction number may be as high as 18 one should vaccinate at least 94.4% of newborns in order to eradicate the disease.
Vacunación e información
Las sociedades modernas están enfrentándose al desafío de la exención “racional", es decir, la decisión de la familia de no vacunar a los niños como consecuencia de una comparación "racional" entre el riesgo percibido por la infección y los posibles daños por la vacuna.Para valorar si este comportamiento es realmente racional, es decir, si esto puede igualmente llevar a la erradicación de la enfermedad, simplemente hay que asumir que la tasa de vacunación es una función creciente del número de sujetos infecciosos:
In such a case the eradication condition becomes:
i.e. the baseline vaccination rate should be greater than the "mandatory vaccination" threshold, which, in case of exemption, cannot hold. Thus, "rational" exemption might be myopic since it is based only on the current low incidence due to high vaccine coverage, instead taking into account future resurgence of infection due to coverage decline.
Vacunación de los no recién nacidos
En el caso de que además haya vacunas a no recién nacidos a una tasa ρ, la ecuación para el sujeto susceptible y vacunado se debe modificar de la siguiente manera :
leading to the following eradication condition:
Estrategia de vacunación frecuente
Esta estrategia vacuna repetidamente a un grupo de edad definido (como niños pequeños o ancianos) en una población susceptible a lo largo del tiempo. Con esta estrategia, se retira inmediatamente al grupo de individuos susceptibles, lo que permite la eliminación de una enfermedad infecciosa, (como el sarampión), de toda la población.Cada unidad de tiempo T, una fracción constante p de sujetos susceptibles se vacunan en un tiempo relativamente corto (respecto a la dinámica de la enfermedad).Esto lleva a las siguientes ecuaciones diferenciales impulsivas para los sujetos susceptibles y vacunados:
It is easy to see that by setting I = 0 one obtains that the dynamics of the susceptible subjects is given by:
and that the eradication condition is:
La influencia de la edad: modelos estructurados por edad
La edad influye profundamente en la propagación de la enfermedad en una población, especialmente en la tasa de contacto.Esta tasa resume la efectividad de los contactos entre sujetos susceptibles e infecciosos.Teniendo en cuenta las edades de las clases epidémicas (to limit ourselves to the susceptible-infectious-removed scheme) such that:
(where is the maximum admissible age) and their dynamics is not described, as one might think, by "simple" partial differential equations, but by integro-differential equations:
where:
is the force of infection, which, of course, will depend, though the contact kernel on the interactions between the ages.
La complejidad se agrega por las condiciones iniciales de los recién nacidos (es decir, por a=0), que son fáciles de infectar y eliminar:
but that are nonlocal for the density of susceptible newborns:
where are the fertilities of the adults.
Además, definiendo ahora la densidad de la población total one obtains:
In the simplest case of equal fertilities in the three epidemic classes, we have that in order to have demographic equilibrium the following necessary and sufficient condition linking the fertility with the mortality must hold:
and the demographic equilibrium is
automatically ensuring the existence of the disease-free solution:
A basic reproduction number can be calculated as the spectral radius of an appropriate functional operator.
Otras consideraciones dentro de los modelos compartimentales epidémicos
Transmisión vertical
En el caso de algunas enfermedades como el SIDA y la Hepatitis B, es posible que la descendencia de los padres infectados nazca con la infección.La transmisión de la enfermedad por medio de la madre se denomina transmisión vertical.La afluencia de miembros adicionales en la categoría infectada puede considerarse dentro del modelo al incluir una fracción de los miembros recién nacidos en el compartimento infectado.
Transmisión vectorial
Las enfermedades transmitidas indirectamente entre seres humanos, - por ejemplo, la malaria que se transmite por medio de mosquitos - se transmiten a través de un vector.En estos casos, las transferencias de infección de humanos al insecto y un modelo epidémico deben incluir ambas especies, generalmente requiriendo más compartimentos que un modelo de transmisión directa.
Otros
Otros casos que necesitan considerarse al modelar una epidemia incluyen cosas como las siguientes: Mezclas no homogéneas Infectividad variable Distribuciones que son espacialmente no uniformes Enfermedades causadas por macroparásitos
Modelos epidémicos determinísticos contra estocásticos
Es importante destacar que los modelos determinísticos que aquí se presentan son válidos únicamente en poblaciones suficientemente grandes y en consecuencia deben ser utilizados con precaución.Para ser más precisos, estos modelos sólo son válidos en el límite termodinámico, donde la población es efectivamente infinita.En modelos estocásticos, el equilibrio endémico a largo plazo obtenido previamente, no se mantiene, ya que existe una probabilidad finita de que el número de individuos infectados disminuya por debajo de uno en un sistema. En un sistema real, el patógeno puede no propagarse, ya que ningún huésped estaría infectado.Sin embargo, en modelos de campo determinísticos, el número de infectados puede asumir valores reales, concretamente, valores no enteros de huéspedes infectados, y el patógeno aún puede persistir en el sistema con un número de huéspedes que es menor a uno, pero más de cero.
Vea también
Modelización matemática en epidemiología Problema de unidad de área modificable Matriz de última generación
Referencias
Lectura adicional
May, Robert M.; Anderson, Roy M. (1991).Las enfermedades infecciosas en humanos: dinámica y control.Oxford: Oxford University Press.ISBN 0-19-854040-x.Capasso, v. (1993).Estructura matemática de sistemas epidémicosBerlin: Springer.ISBN 3-540-56526-4.Vynnycky, p.; White, R. G., eds.( 2010).Una introducción a la modelización de enfermedades infecciosasOxford: Oxford University Press.ISBN 978-0-19-856576-5.
Enlaces externos
Modelo SIR: Experimentos en línea con JSXGraph
- ↑ Hethcote H (2000). «The Mathematics of Infectious Diseases». SIAM Review 42 (4): 599-653. Bibcode:2000SIAMR..42..599H. doi:10.1137/s0036144500371907.
- ↑ a b Harko, Tiberiu; Lobo, Francisco S. N.; Mak, M. K. (2014). «Exact analytical solutions of the Susceptible-Infected-Recovered (SIR) epidemic model and of the SIR model with equal death and birth rates». Applied Mathematics and Computation (en inglés) 236: 184-194. Bibcode:2014arXiv1403.2160H. arXiv:1403.2160. doi:10.1016/j.amc.2014.03.030.
- ↑ Bailey, Norman T. J. (1975). The mathematical theory of infectious diseases and its applications (2nd edición). London: Griffin. ISBN 0-85264-231-8.
- ↑ Sonia Altizer; Nunn, Charles (2006). Infectious diseases in primates: behavior, ecology and evolution. Oxford Series in Ecology and Evolution. Oxford [Oxfordshire]: Oxford University Press. ISBN 0-19-856585-2.
- ↑ Wolfram Research, Inc. «Mathematica, Version 12.1». Champaign IL, 2020.
- ↑ Miller, J.C. (2012). «A note on the derivation of epidemic final sizes». Bulletin of Mathematical Biology 74 (9). section 4.1. PMC 3506030. PMID 22829179. doi:10.1007/s11538-012-9749-6.
- ↑ Miller, J.C. (2017). «Mathematical models of SIR disease spread with combined non-sexual and sexual transmission routes». Infectious Disease Modelling 2 (1). section 2.1.3. PMC 5963332. PMID 29928728. doi:10.1016/j.idm.2016.12.003.
- ↑ Hethcote, Herbert W. (1989). «Three Basic Epidemiological Models». En Levin, Simon A.; Hallam, Thomas G.; Gross, Louis J., eds. Applied Mathematical Ecology. Biomathematics 18. Berlin: Springer. pp. 119-144. ISBN 3-540-19465-7. doi:10.1007/978-3-642-61317-3_5.
- ↑ (p. 19) The SI Model

![{\displaystyle {\begin{aligned}&{\frac {dS}{dt}}=-{\frac {\beta IS}{N}},\\[6pt]&{\frac {dI}{dt}}={\frac {\beta IS}{N}}-\gamma I,\\[6pt]&{\frac {dR}{dt}}=\gamma I,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29728a7d4bebe8197dca7d873d81b9dce954522e)







































![{\displaystyle {\begin{aligned}S(t)&=S(0)e^{-\xi (t)}\\[8pt]I(t)&=N-S(t)-R(t)\\[8pt]R(t)&=R(0)+\rho \xi (t)\\[8pt]\xi (t)&={\frac {\beta }{N}}\int _{0}^{t}I(t^{*})\,dt^{*}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f6ac0eda5b1278f31690939cdfa1f4daa6b1762)










![{\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\Lambda -\mu S-{\frac {\beta IS}{N}}\\[8pt]{\frac {dI}{dt}}&={\frac {\beta IS}{N}}-\gamma I-\mu I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dad81f67db0f075bec720950feaeeb653916028)





![{\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=-{\frac {\beta SI}{N}}+\gamma I\\[6pt]{\frac {dI}{dt}}&={\frac {\beta SI}{N}}-\gamma I\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/605895c64d824511c45ba20ba151ce5b1cec12fc)



![{\displaystyle {\begin{aligned}&{\frac {\beta }{\gamma }}\leq 1\Rightarrow \lim _{t\to +\infty }I(t)=0,\\[6pt]&{\frac {\beta }{\gamma }}>1\Rightarrow \lim _{t\to +\infty }I(t)=\left(1-{\frac {\gamma }{\beta }}\right)N.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05a8022e25ade4141cdf7a411b25dbb8abfc66b9)










![{\displaystyle {\begin{aligned}{\frac {dM}{dT}}&=\Lambda -\delta M-\mu M\\[8pt]{\frac {dS}{dT}}&=\delta M-{\frac {\beta SI}{N}}-\mu S\\[8pt]{\frac {dI}{dT}}&={\frac {\beta SI}{N}}-\gamma I-\mu I\\[8pt]{\frac {dR}{dT}}&=\gamma I-\mu R\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07401153970a3f9f70f53e3c6ccd16bfe72c87e8)



![{\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dE}{dt}}&=\beta {\frac {I}{N}}S-(\mu +a)E\\[8pt]{\frac {dI}{dt}}&=aE-(\gamma +\mu )I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc79ccdb111aeb1f9000625bce95416611414cd9)


![{\displaystyle \left(S(0),E(0),I(0),R(0)\right)\in \left\{(S,E,I,R)\in [0,N]^{4}:S\geq 0,E\geq 0,I\geq 0,R\geq 0,S+E+I+R=N\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3190cc59889dab0e9167d4241c117e8a2cefe0e0)



![{\displaystyle {\begin{aligned}{\frac {dE_{1}}{dt}}&=\beta (t)I_{1}-(\gamma +a)E_{1}\\[8pt]{\frac {dI_{1}}{dt}}&=aE_{1}-(\gamma +\mu )I_{1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4e137f34047a193685ff0b616c6f86e702f677b)

![{\displaystyle {\begin{aligned}{\frac {dS}{dT}}&=\Lambda -{\frac {\beta SI}{N}}-\mu S+\gamma I\\[6pt]{\frac {dE}{dT}}&={\frac {\beta SI}{N}}-(\epsilon +\mu )E\\[6pt]{\frac {dI}{dT}}&=\varepsilon E-(\gamma +\mu )I\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c400c2e342e82c152cacef3141dc8e5840826218)

![{\displaystyle {\begin{aligned}{\frac {dM}{dT}}&=\Lambda -\delta M-\mu M\\[6pt]{\frac {dS}{dT}}&=\delta M-{\frac {\beta SI}{N}}-\mu S\\[6pt]{\frac {dE}{dT}}&={\frac {\beta SI}{N}}-(\varepsilon +\mu )E\\[6pt]{\frac {dI}{dT}}&=\varepsilon E-(\gamma +\mu )I\\[6pt]{\frac {dR}{dT}}&=\gamma I-\mu R\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bf59ff982500a2b882e26d1635ecf9efb74110e)






![{\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N(1-P)-\mu S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dI}{dt}}&=\beta {\frac {I}{N}}S-(\mu +\gamma )I\\[8pt]{\frac {dV}{dt}}&=\mu NP-\mu V\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16f419364493e2d80326c231356c877d1ad5f719)






![{\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N(1-P)-\mu S-\rho S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dV}{dt}}&=\mu NP+\rho S-\mu V\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b556735b37a851da6eeffe357d39ef0e64a20187)

![{\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-\beta {\frac {I}{N}}S,\quad S(nT^{+})=(1-p)S(nT^{-}),&&n=0,1,2,\ldots \\[8pt]{\frac {dV}{dt}}&=-\mu V,\quad V(nT^{+})=V(nT^{-})+pS(nT^{-}),&&n=0,1,2,\ldots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa20fd9c5facbd652241be938c9ac9fb3dae0204)





















