Identidad de Beltrami

La identidad de Beltrami, que lleva el nombre del matemático italiano Eugenio Beltrami (1835-1900), es un caso especial de las ecuaciones de Euler-Lagrange en el cálculo de variaciones.

La ecuación de Euler-Lagrange sirve para obtener un valor extremo de un funcional con la forma

$I[u]=\int _{a}^{b}L[x,u(x),u'(x)]\,dx\,,$

donde $a$ y $b$ son constantes y $u'(x)={\frac {du}{dx}}$.​

Si ${\frac {\partial L}{\partial x}}=0$, entonces la ecuación de Euler-Lagrange se reduce a la identidad de Beltrami,

$L-u'{\frac {\partial L}{\partial u'}}=C\,,$

donde C es una constante.​​

Obtención de la fórmula

Por la regla de la cadena, la derivada de L es

${\frac {dL}{dx}}={\frac {\partial L}{\partial x}}{\frac {dx}{dx}}+{\frac {\partial L}{\partial u}}{\frac {du}{dx}}+{\frac {\partial L}{\partial u'}}{\frac {du'}{dx}}\,.$

Dado que ${\frac {\partial L}{\partial x}}=0$, se puede escribir que

${\frac {dL}{dx}}={\frac {\partial L}{\partial u}}u'+{\frac {\partial L}{\partial u'}}u''\,.$

Se tiene una expresión para ${\frac {\partial L}{\partial u}}$ de la ecuación de Euler-Lagrange,

${\frac {\partial L}{\partial u}}={\frac {d}{dx}}{\frac {\partial L}{\partial u'}}\,$

que se puede sustituir en la expresión anterior por ${\frac {dL}{dx}}$ para obtener

${\frac {dL}{dx}}=u'{\frac {d}{dx}}{\frac {\partial L}{\partial u'}}+u''{\frac {\partial L}{\partial u'}}\,.$

Según la regla del producto, el lado derecho equivale a

${\frac {dL}{dx}}={\frac {d}{dx}}\left(u'{\frac {\partial L}{\partial u'}}\right)\,.$

Al realizar la integración en ambos lados y poner ambos términos en un lado, se obtiene la identidad de Beltrami,

$L-u'{\frac {\partial L}{\partial u'}}=C\,.$

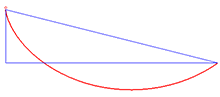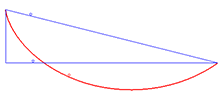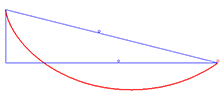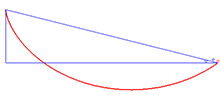
Aplicaciones

Solución al problema de la braquistocrona

La solución al problema de la braquistocrona es la cicloide

Un ejemplo de aplicación de la identidad de Beltrami es la curva braquistócrona, que implica encontrar la curva $y=y(x)$ que minimice la integral

$I[y]=\int _{0}^{a}{\sqrt {{1+y'^{\,2}} \over y}}dx\,.$

El integrando

$L(y,y')={\sqrt {{1+y'^{\,2}} \over y}}$

no depende explícitamente de la variable de integración $x$, por lo que se aplica la identidad de Beltrami,

$L-y'{\frac {\partial L}{\partial y'}}=C\,.$

Sustituyendo por $L$ y simplificando,

$y(1+y'^{\,2})=1/C^{2}~~{\text{(constante)}}\,,$

que se puede resolver con el resultado expresado en forma de ecuación paramétrica

$x=A(\phi -\sin \phi )$

$y=A(1-\cos \phi )$

siendo $A$ la mitad de la constante anterior, ${\frac {1}{2C^{2}}}$ y $\phi$ una variable. Estas son las ecuaciones paramétricas de una cicloide.​

Solución al problema de la catenaria

Una cadena que cuelga de sus extremos forma una catenaria

Considérese una cuerda con densidad uniforme $\mu$ de longitud $l$ suspendida de dos puntos de igual altura y a una distancia $D$. Por la fórmula para la longitud de arco,

$l=\int _{S}dS=\int _{s_{1}}^{s_{2}}{\sqrt {1+y'^{2}}}dx,$

donde $S$ es el arco de la cadena y $s_{1}$ y $s_{2}$ son las condiciones de contorno.

La curva tiene que minimizar su energía potencial:

$U=\int _{S}g\mu y\cdot dS=\int _{s_{1}}^{s_{2}}g\mu y{\sqrt {1+y'^{2}}}dx,$

y está sujeta a la restricción

$\int _{s_{1}}^{s_{2}}{\sqrt {1+y'^{2}}}dx=l,$

donde $g$ es la fuerza de gravedad.

Debido a que la variable independiente $x$ no aparece en el integrando, la identidad de Beltrami se puede usar para expresar la forma de la cadena como una ecuación diferencial de primer orden separable

$L-y\prime {\frac {\partial L}{\partial y\prime }}=\mu gy{\sqrt {1+y\prime ^{2}}}+\lambda {\sqrt {1+y\prime ^{2}}}-\left[\mu gy{\frac {y\prime ^{2}}{\sqrt {1+y\prime ^{2}}}}+\lambda {\frac {y\prime ^{2}}{\sqrt {1+y\prime ^{2}}}}\right]=C,$

donde $\lambda$ es un multiplicador de Lagrange.

Es posible simplificar la ecuación diferencial de la forma siguiente:

${\frac {g\rho y-\lambda }{\sqrt {1+y'^{2}}}}=C.$

Al resolver esta ecuación se obtiene el coseno hiperbólico, donde $C_{0}$ es una segunda constante obtenida de la integración

$y={\frac {C}{\mu g}}\cosh \left[{\frac {\mu g}{C}}(x+C_{0})\right]-{\frac {\lambda }{\mu g}}.$

Las tres incógnitas $C$, $C_{0}$ y $\lambda$ se pueden resolver utilizando las restricciones para los puntos finales de la cadena y la longitud del arco $l$, aunque a menudo es muy difícil obtener una solución de forma cerrada.

Referencias

• Datos: Q125861428