Sistema cristalino triclínico

Un ejemplo de un cristal triclínico, microclino.

En cristalografía, un sistema cristalográfico triclínico es uno de los 7 Sistemas cristalinos. Un sistema cristalográfico esta descrito por tres vectores base. En el sistema triclínico, el cristal está descrito por vectores de longitud desigual, tal como en el sistema ortorrómbico. Además, ninguno de ellos es ortogonal con algun otro.

Triclínico (a ≠ b ≠ c y α ≠ β ≠ γ )

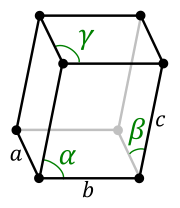
Volumen de una celda

El volumen de un paralelepípedo cuyos lados sean vectores $\vec{a}$, $\vec{b}$, $\vec{c}$ está dado por el triple producto escalar:

$V = | \vec{c} \cdot \left( \vec{a} \times \vec{b} \right) |$

Por conveniencia, colocaremos el vector $\vec{a}$ sobre el eje $x$, y el vector $\vec{b}$ sobre el plano $x y$, entonces tendremos los siguientes vectores:

$\begin{array}{rll} \vec{a} & = \langle a, 0, 0 \rangle & \\ \vec{b} & = \langle b \cos \alpha, b sen \alpha, 0 \rangle & \\ \vec{c} & = \langle c_x, c_y, c_z \rangle & \end{array}$

Para poder hacer el triple producto escalar, es necesario conocer los componentes de $\vec{c}$. Los podemos averiguar haciendo los siguientes productos escalares:

$\vec{a} \cdot \vec{c} = a c_x = a c \cos \beta$

Por lo tanto:

$c_x = c \cos \beta \;$

Enlaces externos

• Wikimedia Commons alberga contenido multimedia sobre Sistema cristalino triclínico. Commons