Tiempo de parada
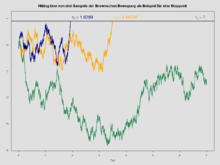
En teoría de la probabilidad, en particular en el estudio de los procesos estocásticos, el tiempo de parada (también conocido como tiempo de Markov) es un tipo específico de «tiempo aleatorio».
La teoría del tiempo de parada puede ser analizada en probabilidad o en estadística, notablemente a través del teorema de la parada opcional. Además, los tiempos de parada son frecuentemente aplicados en pruebas matemáticas para «controlar el continuum de tiempo», como Chung lo expresó en su libro en 1982.
Definición
[editar]Definición discreta
[editar]Se dice que una variable aleatoria es un tiempo de parada respecto de las variables aleatorias si basados en la información proporcionada por podemos determinar si el evento ha ocurrido. El evento no es el único que queda determinado por la información proporcionada por . De hecho, existen otros eventos como .
Otra definición basada en procesos estocásticos es la siguiente: sea una variable aleatoria definida sobre y un proceso estocástico. Si para todo todos los eventos están determinados totalmente por los elementos se dice que es un tiempo de parada. También recibe el nombre de tiempo de Markov.
Definición usando filtraciones
[editar]Sea un espacio de probabilidad filtrado, donde es un conjunto de índices, a menudo o . Un tiempo de parada es una variable aleatoria tal que para todo .
El tiempo de parada tiene lugar en la teoría de la decisión, en la cual una regla de parada se caracteriza como un mecanismo que sirve para decidir si continuar o detener un proceso sobre la base de la posición presente y de eventos pasados, y que casi seguramente conduce a una decisión para detener en algún momento de tiempo.
Bibliografía
[editar]- Chung, Kai Lai (1982). Lectures from Markov processes to Brownian motion. Grundlehren der Mathematischen Wissenschaften No. 249. Nueva York: Springer-Verlag. ISBN 0-387-90618-5.
- Fischer, Tom (2013). «On simple representations of stopping times and stopping time sigma-algebras». Statistics and Probability Letters 83 (1): 345-349. doi:10.1016/j.spl.2012.09.024.
- Revuz, Daniel and Yor, Marc (1999). Continuous martingales and Brownian motion. Grundlehren der Mathematischen Wissenschaften No. 293 (Tercera edición edición). Berlín: Springer-Verlag. ISBN 3-540-64325-7.
- H. Vincent Poor and Olympia Hadjiliadis (2008). Quickest Detection (Primera edición edición). Cambridge: Cambridge University Press. ISBN 978-0-521-62104-5.
- Protter, Philip E. (2005). Stochastic integration and differential equations. Stochastic Modelling and Applied Probability No. 21 (Segunda edición (versión 2.1, corregida tercera impresión) edición). Berlín: Springer-Verlag. ISBN 3-540-00313-4.
Enlaces externos
[editar]- Esta obra contiene una traducción derivada de «Stopping time» de Wikipedia en inglés, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.















