Diferencia entre revisiones de «Silla de mono»

Contenido eliminado Contenido añadido

En renglón

Revisión del 18:21 18 sep 2023

En matemáticas, la silla de mono (monkey saddle en inglés) es una superficie definida por la ecuación:

z=x^{3}-3xy^{2},\,

o en coordenadas cilíndricas:

z=\rho ^{3}\cos(3\varphi ).

Pertenece a la clase de superficies con puntos de ensilladura y su nombre deriva de la observación de que una silla de montar para un mono requeriría dos depresiones para las patas y otra para la cola. El punto Plantilla:Tmath en la silla de montar corresponde a un punto crítico degenerado de la función Plantilla:Tmath en Plantilla:Tmath. La silla de montar tiene un punto umbilical aislado con curvatura de Gauss cero en el origen, mientras que la curvatura es estrictamente negativa en todos los demás puntos.

Se pueden relacionar las ecuaciones rectangulares y cilíndricas usando números complejos $x+iy=re^{i\varphi }:$

z=x^{3}-3xy^{2}=\operatorname {Re} [(x+iy)^{3}]=\operatorname {Re} [r^{3}e^{3i\varphi }]=r^{3}\cos(3\varphi ).

Al reemplazar 3 en la ecuación cilíndrica por cualquier número entero Plantilla:Tmath, se puede crear una silla con Plantilla:Tmath depresiones.^[1]

Otra orientación de la silla de mono es el pétalo de Smelt, definido por la ecuación $x+y+z+xyz=0,$ de manera que el eje z- de la silla de mono corresponde a la dirección Plantilla:Tmath en el pétalo de Smelt.^[2]^[3]

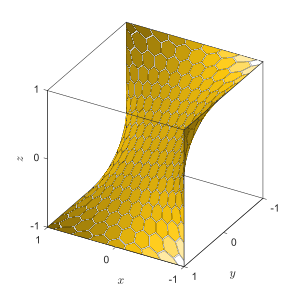
Silla de montar

El término "silla de montar a caballo" puede usarse en contraste con la silla de mono, para designar una superficie de silla ordinaria en la que "z"(x,y) tiene un punto de silla, un mínimo local. o máximo en cada dirección del plano xy. Por el contrario, la silla de mono posee un punto de inflexión estacionario en todas las direcciones.

Referencias

↑ Peckham, S.D. (2011) Monkey, starfish and octopus saddles, Proceedings of Geomorphometry 2011, Redlands, CA, pp. 31-34, https://www.researchgate.net/publication/256808897_Monkey_Starfish_and_Octopus_Saddles
↑ J., Rimrott, F. P. (1989). Introductory Attitude Dynamics. New York, NY: Springer New York. p. 26. ISBN 9781461235026. OCLC 852789976.
↑ Chesser, H.; Rimrott, F.P.J. (1985). «Magnus Triangle and Smelt Petal». En Rasmussen, H., ed. CANCAM '85: Proceedings, Tenth Canadian Congress of Applied Mechanics, June 2-7, 1985, the University of Western Ontario, London, Ontario, Canada.

Enlaces externos

Weisstein, Eric W. «Monkey Saddle». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.

Datos: Q382375

[1] Peckham, S.D. (2011) Monkey, starfish and octopus saddles, Proceedings of Geomorphometry 2011, Redlands, CA, pp. 31-34, https://www.researchgate.net/publication/256808897_Monkey_Starfish_and_Octopus_Saddles

[2] J., Rimrott, F. P. (1989). Introductory Attitude Dynamics. New York, NY: Springer New York. p. 26. ISBN 9781461235026. OCLC 852789976.

[3] Chesser, H.; Rimrott, F.P.J. (1985). «Magnus Triangle and Smelt Petal». En Rasmussen, H., ed. CANCAM '85: Proceedings, Tenth Canadian Congress of Applied Mechanics, June 2-7, 1985, the University of Western Ontario, London, Ontario, Canada.

[1]

[2]

[3]