Kayles

Una fila de bolos. En su turno, un jugador puede optar por eliminar un solo pin o dos adyacentes.

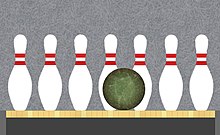
Kayles es un juego imparcial simple en la teoría de juegos combinatorios, inventado por Henry Dudeney en 1908. Dada una fila de bolos imaginarios, los jugadores se turnan para eliminar uno o dos bolos adyacentes, hasta que todos los bolos desaparezcan. Usando la notación de juegos octales, Kayles se denota 0.77.

Reglas

Kayles se juega con una fila de fichas, que representan bolos. La fila puede tener cualquier longitud. Los dos jugadores se alternan; cada jugador, en su turno, puede quitar cualquier pin (una bola lanzada directamente en ese pin), o dos pins adyacentes (una bola lanzada para golpear a ambos). Según la convención de juego normal, un jugador pierde cuando no tiene un movimiento legal (es decir, cuando todos los pines se han ido). El juego también se puede jugar usando las reglas de misère; en este caso, el jugador que no puede moverse gana.

Historia

Kayles fue inventado por Henry Dudeney.​​ Richard Guy y Cedric Smith fueron los primeros en analizar completamente la versión de juego normal, utilizando la teoría de Sprague-Grundy.​​ La versión misère fue analizada por William Sibert en 1973, pero no publicó su trabajo hasta 1989.​

El nombre "Kayles" es una anglicización del francés quilles, que significa "bolos".

Análisis

La mayoría de los jugadores descubren rápidamente que el primer jugador tiene una victoria garantizada en Kayles normales siempre que la longitud de la fila sea mayor que cero. Esta victoria se puede lograr mediante una estrategia de simetría . En su primer movimiento, el primer jugador debe moverse de modo que la fila se divida en dos secciones de igual longitud. Esto restringe todos los movimientos futuros a una sección u otra. Ahora, el primer jugador simplemente imita los movimientos del segundo jugador en la fila opuesta.

Es más interesante preguntar cuál es el valor nim de una fila de longitud $n$. Esto a menudo se denota $K_{n}$; es un nimber, no un número. Según el teorema de Sprague-Grundy, $K_{n}$ es la Mex sobre todos los movimientos posibles de la nim-suma de los valores de nim de las dos secciones resultantes. Por ejemplo,

$K_{5}={\mbox{mex}}\{K_{0}+K_{4},K_{1}+K_{3},K_{2}+K_{2},K_{0}+K_{3},K_{1}+K_{2}\},\,$

porque de una fila de longitud 5, se puede pasar a las posiciones

$K_{0}+K_{4},\quad K_{1}+K_{3},\quad K_{2}+K_{2},\quad K_{0}+K_{3},{\text{ y}}K_{1}+K_{2}.\,$

Cálculo recursivo de valores (comenzando con $K_{0}=0$) da los resultados resumidos en la siguiente tabla. Para encontrar el valor de $K_{n}$ en la mesa, escribe $n$ como $12a+b$, y observe la fila a, columna b:

Kayles nim-valores a través de $K_{83}$

$K_{n}$	0	1	2	3	4	5	6	7	8	9	10	11
0+	0	1	2	3	1	4	3	2	1	4	2	6
12+	4	1	2	7	1	4	3	2	1	4	6	7
24+	4	1	2	8	5	4	7	2	1	8	6	7
36+	4	1	2	3	1	4	7	2	1	8	2	7
48+	4	1	2	8	1	4	7	2	1	4	2	7
60+	4	1	2	8	1	4	7	2	1	8	6	7
72+	4	1	2	8	1	4	7	2	1	8	2	7

En este punto, la secuencia de valores nim se vuelve periódica​ con el período 12, por lo que todas las demás filas de la tabla son idénticas a la última fila.

Aplicaciones

Debido a que ciertas posiciones en Puntos y Cuadros se reducen a posiciones de Kayles,​ es útil entender a Kayles para analizar una posición genérica de Puntos y Cuadros.

Complejidad computacional

En un juego normal, Kayles se puede resolver en tiempo polinomial utilizando la teoría de Sprague-Grundy.​

Los nodos de Kayles es una generalización de Kayles a grafos en los que cada cuenco "derriba" (elimina) un vértice deseado y todos sus vértices vecinos. (Alternativamente, este juego puede verse como dos jugadores que encuentran juntos un conjunto independiente). Schaefer (1978)​ emostró que decidir el resultado de este juego es PSPACE-completo. El mismo resultado es válido para una versión partidista del nodo Kayles, en la que, para cada nodo, solo uno de los jugadores puede elegir ese nodo en particular como objetivo de derribo.

Véase también

• Teoría de juegos combinatorios
• Juego octal

• Kayles de Dawson

• Nimber

Referencias

• Datos: Q6380627