Teoría de Mohr-Coulomb
La teoría de Mohr-Coulomb es un modelo matemático (ver Superficie de fluencia) que describe la respuesta de materiales quebradizos, tales como hormigón, o agregados de partículas como el suelo,[1] a esfuerzo cortante, así como tensión normal. La mayoría de los materiales en ingeniería clásica se comportan siguiendo esta teoría al menos en una parte del corte. En general, la teoría se aplica a los materiales para los que la resistencia a la compresión es muy superior a la resistencia a la tracción, caso de los materiales cerámicos. La teoría explica que el corte de un material se produce para una combinación entre tensión normal y tensión tangencial, y que cuanto mayor sea la tensión normal, mayor será la tensión tangencial necesaria para cortar el material.[2]
Aplicaciones[editar]
En Ingeniería geotécnica se utiliza para definir resistencia al corte de suelos y rocas en diferentes casos de tensión efectiva.
En la ingeniería estructural se utiliza para determinar la carga de rotura, así como el ángulo de la rotura de una fractura de desplazamiento en materiales cerámicos y similares (como el hormigón). La hipótesis de Coulomb se emplea para determinar la combinación de esfuerzo cortante y normal que causa una fractura del material. El círculo de Mohr se utiliza para determinar los ángulos donde esas tensiones sean máximas. Generalmente la rotura se producirá para el caso de tensión principal máxima.
Modelo[editar]

Criterio de fallo de Mohr-Coulomb[editar]
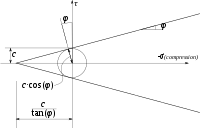
El criterio de fallo de Mohr-Coulomb[3] se representa por la envolvente lineal de los círculos de Mohr que se producen en la rotura. La relación de esa envolvente se expresa como
donde:
- es el esfuerzo cortante.
- es la tensión de normal.
- es la intersección de la línea de fallo con el eje de , llamada cohesión.
- es la pendiente del ángulo de la envolvente, también llamado el ángulo de rozamiento interno.
La compresión se asume positiva para el esfuerzo de compresión, aunque también se puede estudiar el caso con la tensión negativa cambiando el signo de
Si , el criterio de Mohr-Coulomb se reduce al criterio de Tresca. Si el modelo de Mohr-Coulomb es equivalente al modelo de Rankine. Valores más altos de no están permitidos.
De los círculos de Mohr tenemos:
donde
y es la tensión máxima principal y es la tensión mínima principal.
De esta forma el criterio de Mohr-Coulomb puede expresarse también como:
Esta es la forma del criterio de Mohr-Coulomb aplicable al fallo en un plano paralelo a la dirección .
Criterio de fallo de Mohr-Coulomb en tres dimensiones[editar]
El criterio de Mohr-Coulomb se expresa en las tres dimensiones como:
La superficie de falla quedaría como un cono de sección hexagonal.
Las expresiones para y puede ser generalizada para tres dimensiones mediante el desarrollo de expresiones para la tensión normal y la tensión cortante en un plano de orientación arbitraria respecto a un eje de coordenadas. Si el vector unitario normal al plano es
donde son los tres vectores ortonormales, y las tensiones principales están alineadas con los vectores de la base , entonces la expresiones para son
El criterio de Mohr Coulomb se puede usar en su expresión generalizada
para los seis planos con tensión máxima de corte tangencial.
Una mejora común de este modelo es la combinación de hipótesis de fricción de Coulomb con la hipótesis de tensión principal de Rankine para describir una fractura de separación.
Véase también[editar]
Referencias[editar]
- ↑ efunda. «Maximum Normal Stress Criterion».
- ↑ Granular Volcano Group. «A Review of Plastic-Frictional Theory Part. 1». Archivado desde el original el 9 de mayo de 2012.
- ↑ Coulomb, C. A. (1776). Essai sur une application des regles des maximis et minimis a quelquels problemesde statique relatifs, a la architecture. Mem. Acad. Roy. Div. Sav., vol. 7, pp. 343–387.














![{\displaystyle \left\{{\begin{aligned}\pm {\cfrac {\sigma _{1}-\sigma _{2}}{2}}&=\left[{\cfrac {\sigma _{1}+\sigma _{2}}{2}}\right]\sin(\phi )+c\cos(\phi )\\\pm {\cfrac {\sigma _{2}-\sigma _{3}}{2}}&=\left[{\cfrac {\sigma _{2}+\sigma _{3}}{2}}\right]\sin(\phi )+c\cos(\phi )\\\pm {\cfrac {\sigma _{3}-\sigma _{1}}{2}}&=\left[{\cfrac {\sigma _{3}+\sigma _{1}}{2}}\right]\sin(\phi )+c\cos(\phi )\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2aba1cf9ae41f434ba4a904d6ca5bb1011a8fd9d)





