Sistema de masa variable

En Mecánica, un sistema de masa variable es un conjunto de materia cuya masa varía con el tiempo. La Segunda Ley de Newton no se puede aplicar directamente dado que sólo es válida para sistemas de masa constante.[1][2] Por lo tanto, la dependencia de la masa m respecto del tiempo se analizará tratando al sistema como si de uno cerrado se tratase; esto significa considerar un sistema que contenga tanto a la masa principal como a la masa variante. Al añadir un término que considera el momento de la masa que se adhiere o desprende, la ecuación general de movimiento de una masa variable (que expresa el cambio del momento respecto al tiempo) puede escribirse como:
Donde Fext es la fuerza neta externa ejercida en el sistema cerrado, vrel es la velocidad relativa de la masa que está escapando o ingresando con respecto al centro de masa del cuerpo, y v es la velocidad del cuerpo.[1] En la ingeniería aeroespacial, la cual estudia la mecánica de los cohetes, el término vrel se lo llama la velocidad efectiva de escape y se denomina como ve.[3]
Un error de concepto frecuente es que un sistema de masa variable puede describirse como la derivada respecto del tiempo del producto de la masa con la velocidad, ya que la fuerza neta externa es el cambio en el momento respecto del tiempo. Si bien este hecho no cambia, en un sistema abierto la variación del momento ya no puede describirse como el cambio en el producto de la masa con la velocidad, pues al hacerlo se estaría olvidando al impulso asociado a la variación de masa del sistema. Dado que estos sistemas, como el del cohete que pierde combustible y eyecta gases, no son sistemas cerrados y dado que la masa no se debe tratar como una variable en función del tiempo, la siguiente fórmula no es correcta:
La falacia de esta fórmula puede verse en que no respeta la Invariancia galileana la cual sostiene que un objeto de masa variable con F = 0 en un marco de referencia, tendrá F ≠ 0 en otro.
Deducción de la fórmula[editar]
Existen distintas derivaciones para la ecuación de movimiento del sistema de masa variable, que depende de si la masa está escapando o ingresando al cuerpo (en otras palabras, si la masa del cuerpo está aumentando o disminuyendo). Para simplificar los cálculos, tratamos a los cuerpos como puntuales. También se asume que la masa no es capaz de aplicarle una fuerza externa al cuerpo fuera del evento de acreción/ablación.
Caso acreción de masa[editar]
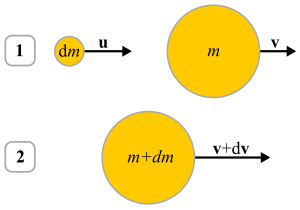
La siguiente derivación es para un cuerpo que está ganando masa. Un cuerpo con masa variable en el tiempo m se mueve con velocidad v a un tiempo inicial t. En el mismo instante, una partícula de masa dm se mueve con una velocidad u. El momento inicial se puede escribir como:[4]
Ahora, a un tiempo t + dt, el cuerpo principal y la masa puntual se acrecientan en un solo cuerpo de velocidad v + dv. Por lo tanto, el nuevo momento del sistema quedaría:
Como dmdv es el producto de dos valores muy pequeños, este término se puede despreciar. Es decir que para un cierto dt el momento del sistema sería:
Entonces, por la segunda ley de Newton:
Fijarse en que u - v es la velocidad de dm relativa a m, simbolizada como vrel, esta ecuación final se puede reescribir como:[5]
Caso ablación/eyección de masa[editar]
En un sistema en el que la masa está saliendo de un cuerpo, la deducción varía ligeramente. A un tiempo t, una masa m viaja a una velocidad v, por lo tanto el momento inicial del sistema viene dado por:
Como el cuerpo principal va a estar perdiendo masa, dm será negativo, esto significa que para un tiempo t + dt el momento de sistema será:
donde u es la velocidad de la masa eyectada. Por tanto, en dt el momento del sistema es:
Ya verificamos que el dp es el mismo en ambos casos; es decir, la conclusión es la misma y la fórmula se mantiene.[4]
Formas de expresión[editar]

Por definición, la aceleración está dada por a = dv/dt, entonces la ecuación de movimiento de un sistema de masa variable se puede escribir:
Para cuerpos que no son tratados como masas puntuales, a debe ser reemplazado por acm, la aceleración del centro de masa del sistema, es decir:
La fuerza debida a un empuje se suele definir como de manera que:
Esta forma nos muestra que un cuerpo puede tener aceleración debida a un empuje, incluso si no actúan fuerzas en él. (Fext = 0). Nótese finalmente que si tomamos Fnet como la suma de Fext y Fempuje entonces la ecuación retoma la forma usual de la segunda ley de Newton
Referencias[editar]
- ↑ a b Plastino, Angel R.; Muzzio, Juan C. (1992). «On the use and abuse of Newton's second law for variable mass problems». Celestial Mechanics and Dynamical Astronomy (Netherlands: Kluwer Academic Publishers) 53 (3): 227-232. Bibcode:1992CeMDA..53..227P. ISSN 0923-2958. doi:10.1007/BF00052611. Consultado el 30 de diciembre de 2011.
- ↑ Basavaraju, G; Ghosh, Dipin (1 de febrero de 1985). Mechanics and Thermodynamics. Tata McGraw-Hill. pp. 162-165. ISBN 978-0-07-451537-2.
- ↑ Benson, Tom. «Ideal Rocket Equation». NASA. Archivado desde el original el 7 de diciembre de 2014. Consultado el 30 de diciembre de 2011.
- ↑ a b Cveticanin, L (21 de octubre de 1998). Dynamics of Machines with Variable Mass (1 edición). CRC Press. pp. 15-20. ISBN 978-90-5699-096-1.
- ↑ Giancoli, Douglas C. (2008). Physics for Scientists & Engineers 2 (4, illustrated edición). Pearson Education. pp. 236-238. ISBN 978-0-13-227359-6.


![{\displaystyle \mathbf {F} _{\mathrm {net} }={\frac {\mathrm {d} }{\mathrm {d} t}}{\big [}m(t)\mathbf {v} (t){\big ]}=m(t){\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}+\mathbf {v} (t){\frac {\mathrm {d} m}{\mathrm {d} t}}\qquad \mathrm {(Incorrecto)} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c87ad2dfd95a8e9987e3e346db2298f9ef54b1f)











