Reflexión deslizada


En geometría bidimensional, una reflexión deslizada (también traslareflexión, reflexión deslizante o reflexión con deslizamiento) es una operación de simetría que consiste en aplicar sucesivamente una reflexión respecto a una recta y una traslación en el sentido de esa misma recta, combinadas en una sola operación. Los objetos con simetría de deslizamiento, en general, no son simétricos respecto a una reflexión. En teoría de grupos, el plano de deslizamiento se clasifica como un tipo de isometría opuesta bidimensional.[1]
La sucesión de reflexiones deslizadas está relacionada con la generación de frisos. Un reflejo deslizado se puede ver como un caso límite de una rotoreflexión, cuando la rotación se convierte en una traslación. Según la notación de Schoenflies, se describe como S2∞, en la notación de Coxeter tiene la forma [∞+, 2+]; y en la notación orbifold se escribe como ∞ ×.[1]
Descripción[editar]
La combinación de una reflexión respecto a una recta y una traslación en una dirección perpendicular, se convierte en una reflexión equivalente respecto a una recta paralela a la original. Sin embargo, una reflexión deslizada no puede ser reducida de esa manera. Por lo tanto, el efecto de una reflexión combinada con una traslación cualquiera es una reflexión deslizada, con un solo caso especial reducible a una nueva reflexión. Estos son los dos tipos de isometrías en 2D indirectas.
Por ejemplo, existe una isometría que consiste en la reflexión sobre el eje x, seguida de la traslación de una unidad paralela a ella. En coordenadas cartesianas, se expresa como
- (x, y) → (x+1, -y).
Esta aplicación conserva el paralelismo entre rectas paralelas.
El grupo de isometría generado por una única reflexión deslizada es un grupo cíclico infinito.[1]
La combinación de dos reflexiones de deslizamiento iguales genera una traslación pura, con un vector de traslación que es el doble del desplazamiento de la reflexión deslizada, por lo que las combinaciones pares de reflexiones deslizadas forman un grupo de traslaciones.
En el caso de la simetría de reflexión deslizante, el grupo de simetría de un objeto contiene una reflexión deslizada y, por lo tanto, el grupo generado por esta. Si eso es todo lo que contiene, este tipo de movimiento se clasifica como un friso p11g.
Ejemplo de patrón con este grupo de simetría:
Grupo friso n. 6 (reflexiones de deslizamiento, traslaciones y rotaciones) se genera mediante una reflexión deslizada y una rotación alrededor de un punto en la línea de reflexión. Es isomorfo a un producto semidirecto de Z y C2.
Ejemplo de patrón con este grupo de simetría:
Un ejemplo típico de reflexión deslizada en la vida cotidiana serían las huellas dejadas en la arena por una persona que camina en una playa.
Para cualquier grupo de simetría que contenga alguna simetría de reflexión deslizada, su vector de traslación asociado es la mitad de un elemento del grupo de traslación. Si el vector de traslación de una reflexión deslizada es en sí mismo un elemento del grupo de traslación, entonces la simetría de reflexión deslizada correspondiente se reduce a una combinación de eje de simetría y simetría traslacional.
La simetría de reflexión deslizante con respecto a dos líneas paralelas con la misma traslación implica que también hay simetría traslacional en la dirección perpendicular a estas líneas, con una distancia de traslación que es el doble de la distancia entre las líneas de reflexión deslizada. Esto corresponde al grupo del papel pintado pg; también se da con simetría adicional en pmg, pgg y p4g.
Si también hay líneas de reflexión verdaderas en la misma dirección, entonces están espaciadas uniformemente entre las líneas de reflexión deslizadas. Una línea de reflexión deslizada paralela a una línea de reflexión verdadera implica esta situación. Esto corresponde al grupo de papel pintado cm. La simetría de traslación viene dada por los vectores de traslación oblicuos de un punto en una línea de reflexión verdadera a dos puntos en el siguiente, apoyando un rombo con la línea de reflexión verdadera como una de las diagonales. Con simetría adicional, también ocurre en cmm, p3m1, p31m, p4m y p6m.
En 3D, la reflexión deslizada se denomina plano de deslizamiento. Es un reflejo en un plano combinado con una traslación paralela al plano.
Grupos del papel pintado[editar]
En el plano euclídeo, 3 de 17 elementos del grupo del papel pintado requieren generadores de reflexión deslizada. El elemento p2gg posee reflexiones deslizadas ortogonales y rotaciones de dos lóbulos. El elemento cm posee simetrías de deslizamiento paralelas, y pg posee deslizamientos paralelos (las reflexiones de deslizamiento se muestran a continuación como líneas discontinuas)
| Nombre cristalográfico | pgg | cm | pg |
|---|---|---|---|
| Nombre de Conway | 22× | *× | ×× |
| Diagrama | 
|

|
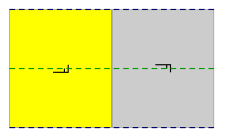
|
| Ejemplo | 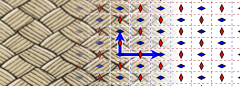
|

|

|
Reflexión deslizada en la naturaleza y juegos[editar]
La simetría de deslizamiento se puede observar en la naturaleza entre ciertos fósiles del periodo Ediacárico; los machaeridias; y ciertos gusanos palaeoscolecidos.[2] También se puede ver en muchos grupos existentes de pennatulaceas.[3]
La reflexión deslizada es común en determinadas modelizaciones de ordenador, como los juegos de la vida, propiciando la formación de cañones que generan patrones compactos de puntos que se desplazan en línea recta por la pantalla de la simulación.
Véase también[editar]
- Eje helicoidal, plano de deslizamiento para las operaciones de simetría 3D correspondientes
Referencias[editar]
- ↑ a b c Martin, George E. (1982), Transformation Geometry: An Introduction to Symmetry, Undergraduate Texts in Mathematics, Springer, p. 64, ISBN 9780387906362..
- ↑ Waggoner, B. M. (1996). «Phylogenetic Hypotheses of the Relationships of Arthropods to Precambrian and Cambrian Problematic Fossil Taxa». Systematic Biology 45 (2): 190-222. JSTOR 2413615. doi:10.2307/2413615.
- ↑ Zubi, Teresa (2 de enero de 2016). «Octocorals (Stoloniferans, soft corals, sea fans, gorgonians, sea pens) - Starfish Photos - Achtstrahlige Korallen (Röhrenkorallen, Weichkorallen, Hornkoralllen, Seefedern, Fächerkorallen)». starfish.ch. Consultado el 8 de septiembre de 2016.
