Notación Voigt

En matemáticas, la notación Voigt o forma de Voigt es una manera de representar un tensor simétrico reduciendo su orden.​ El método se basa en la simetría para almacenar solo los valores no repetidos y lograr una representación con menos valores, lo que facilita especialmente el cálculo en elementos de elevado rango.

Existen diversas variantes, algunas de las cuales reciben nombres específicos como notación Mandel, notación Mandel-Voigt y notación Nye. De forma similar, existe una notación Kelvin basada en el trabajo de Helbig sobre ideas de Lord Kelvin.​ La diferencia entre los diferentes métodos se debe a diferentes elecciones de pesos (dado que el método original no permite realizar algunas operaciones con la forma reducida, se plantearon variantes que sí lo permitieron) y su uso tradicional en diferentes campos.

Ejemplos

Por ejemplo, un tensor simétrico 2x2 X sólo tiene tres elementos distintos, el dos en la diagonal y otro fuera de ella. Por ello pueda ser expresado como el vector

$\langle x_{11},x_{22},x_{12}\rangle$.

Similarmente, el tensor de tensión (en notación matricial) está definido por:

${\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\end{matrix}}\right].$

En notación Voigt dicho tensor queda definida por sus seis valores diferentes:

${\tilde {\sigma }}=(\sigma _{xx},\sigma _{yy},\sigma _{zz},\sigma _{yz},\sigma _{xz},\sigma _{xy})\equiv (\sigma _{1},\sigma _{2},\sigma _{3},\sigma _{4},\sigma _{5},\sigma _{6}).$

El tensor de deformaciones, similar en naturaleza al tensor de tensión tiene una expresión semejante:

${\boldsymbol {\epsilon }}=\left[{\begin{matrix}\epsilon _{xx}&\epsilon _{xy}&\epsilon _{xz}\\\epsilon _{yx}&\epsilon _{yy}&\epsilon _{yz}\\\epsilon _{zx}&\epsilon _{zy}&\epsilon _{zz}\end{matrix}}\right].$

Cuya forma Voigt es

${\tilde {\epsilon }}=(\epsilon _{xx},\epsilon _{yy},\epsilon _{zz},\gamma _{yz},\gamma _{xz},\gamma _{xy})\equiv (\epsilon _{1},\epsilon _{2},\epsilon _{3},\epsilon _{4},\epsilon _{5},\epsilon _{6}),$

Donde $\gamma _{xy}=2\epsilon _{xy}$, $\gamma _{yz}=2\epsilon _{yz}$, and $\gamma _{zx}=2\epsilon _{zx}$ relacionan los valores con las magnitudes observables en ingeniería mediante pesos.

Asimismo, un tensor simétrico de cuarto orden puede ser reducido a una matriz 6x6.

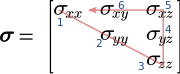
Regla mnemotécnica

Una regla mnemotécnica sencilla para memorizar los índices de la notación Voigt es:

• Escribir el tensor en forma matricial
• Contar la diagonal
• Continuar en la última columna
• Volver al primer elemento a lo largo de la primera fila.

Notación Mandel

Para un tensor simétrico de segundo orden.

Sólo seis componentes son distintos, los tres en la diagonal y otros tres fuera de ella. Por ello, el tensor puede ser expresado:

La ventaja principal de la notación Mandel es que permite el uso de las mismas operaciones convencionales que los vectores, por ejemplo:

Aplicaciones

La notación recibe su nombre en honor al físico Woldemar Voigt. Es útil, por ejemplo, en los cálculos que implican modelos constitutivos para simular materiales, como ley de Hooke generalizada, así como el método de elementos finitos o métodos de imágenes médicas.​​

La ley de Hooke tiene tensor de rigidez simétrico de cuarto orden de 81 componentes (3×3×3×3). La notación Voigt permite trabajar con una 6×6. Aun así, la forma Voigt no preserva la suma de los cuadrados, lo que en el caso de la ley de Hooke tiene implicaciones geométricas. Esto motiva la introducción de los pesos para convertir el mapeo una isometría.

Una discusión sobre la invariancia de las notaciones de Voigt y Mandel puede hallarse en Helnwein (2001).​

Véase también

• Ley de elasticidad de Hooke

Referencias

• Datos: Q1411409
• Multimedia: Voigt notation / Q1411409