Ley esférica de los cosenos

Triángulo esférico resuelto por la ley de los cosenos

En trigonometría esférica, la ley de los cosenos (también llamada regla del coseno para los lados^[1]) es un teorema que relaciona los lados y los ángulos de un triángulo esférico, análogo al teorema del coseno ordinario del plano en trigonometría.

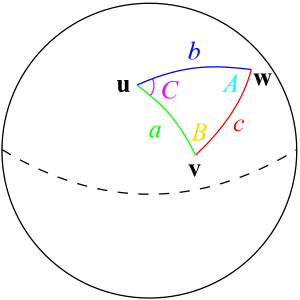
Dada una esfera unitaria, un "triángulo esférico" en la superficie de la esfera está definido por las circunferencias máximas que conectan tres puntos $u, v$ y $w$ en la esfera (según la imagen). Si las longitudes de estos tres lados son $a$ (de $u$ a $v), b$ (de $u$ a $w$ ) y $c$ (de $v$ a $w$ ), y el ángulo de la esquina opuesta a $c$ es $C$ , entonces la (primera) ley esférica de los cosenos establece que:^[2]^[1]

\cos c=\cos a\cos b+\operatorname {sen} a\operatorname {sen} b\cos C\,

Como se trata de una esfera unitaria, las longitudes $a, b$ y $c$ son simplemente iguales a los ángulos (en radianes) subtendidos por esos lados desde el centro de la esfera. Para una esfera no unitaria, las longitudes son los ángulos subtendidos multiplicados por el radio, y la fórmula sigue siendo válida si $a, b$ y $c$ se reinterpretan como ángulos subtendidos. Como caso especial, para $C = π / 2$ , luego $cos C = 0$ , y se obtiene el análogo esférico del teorema de Pitágoras:

\cos c=\cos a\cos b\,

Si se usa la ley de los cosenos para resolver $c$ , la necesidad de invertir el coseno aumenta el error de redondeo cuando $c$ es pequeño. En este caso, es preferible la expresión alternativa de la fórmula del semiverseno.^[3]

Una variación de la ley de los cosenos, la segunda ley esférica de los cosenos,^[4] (también llamada regla del coseno para ángulos^[1]) establece que:

\cos C=-\cos A\cos B+\operatorname {sen} A\operatorname {sen} B\cos c\,

donde $A$ y $B$ son los ángulos de las esquinas opuestas a los lados $a$ y $b$ , respectivamente. Se puede obtener considerando un triángulo esférico dual con el dado.

Demostraciones[editar]

Primera demostración[editar]

Se denominan $u, v$ y $w$ a los vectores unitarios desde el centro de la esfera hasta las esquinas del triángulo. Los ángulos y las distancias no cambian si se gira el sistema de coordenadas, por lo que se puede girar el sistema de coordenadas de modo que $\mathbf {u}$ esté en polo norte y $\mathbf {v}$ esté en algún lugar del meridiano cero (longitud 0). Con esta rotación, las coordenadas esféricas para $\mathbf {v}$ son $(r,\theta ,\phi )=(1,a,0)$ , donde θ es el ángulo medido desde el polo norte, no desde el ecuador, y las coordenadas esféricas para $\mathbf {w}$ son $(r,\theta ,\phi )=(1,b,C)$ . Las coordenadas cartesianas para $\mathbf {v}$ son $(x,y,z)=(\operatorname {sen} a,0,\cos a)$ y las coordenadas cartesianas para $\mathbf {w}$ son $(x,y,z)=(\operatorname {sen} b\cos C,\operatorname {sen} b\operatorname {sen} C,\cos b)$ . El valor de $\cos c$ es el producto escalar de los dos vectores cartesianos, que es $\operatorname {sen} a\operatorname {sen} b\cos C+\cos a\cos b$ .

Segunda demostración[editar]

Sean $u, v$ y $w$ los vectores unitarios desde el centro de la esfera hasta las esquinas del triángulo. Se tiene que $u \cdot u = 1$ , $v \cdot w = cos c$ , $u \cdot v = cos a$ y $u \cdot w = cos b$ . Los vectores $u \times v$ y $u \times w$ tienen longitudes $sen a$ y $sen b$ respectivamente y el ángulo entre ellos es $C$ , entonces

sen a sen b cos C = (u \times v) \cdot (u \times w) = (u \cdot u)(v \cdot w) - (u \cdot v)(u \cdot w) = cos c - cos a cos b

,

utilizando productos vectoriales, productos escalaress y la identidad de Binet-Cauchy $(p \times q) \cdot (r \times s) = (p \cdot r)(q \cdot s) - (p \cdot s)(q \cdot r)$ .

Reordenamientos[editar]

La primera y segunda leyes esféricas de los cosenos se pueden reorganizar para colocar los lados ( $a, b, c$ ) y los ángulos ( $A, B, C$ ) en lados opuestos de las ecuaciones:

{\begin{aligned}\cos C&={\frac {\cos c-\cos a\cos b}{\operatorname {sen} a\operatorname {sen} b}}\\\\\cos c&={\frac {\cos C+\cos A\cos B}{\operatorname {sen} A\operatorname {sen} B}}\\\end{aligned}}

Límite plano: ángulos pequeños[editar]

Para triángulos esféricos pequeños, es decir, para $a, b$ y $c$ pequeños, la ley esférica de los cosenos es aproximadamente la misma que la ley ordinaria de los cosenos en el plano,

c^{2}\approx a^{2}+b^{2}-2ab\cos C\,.

Para probar esto, se usa la aproximación para ángulos pequeños obtenida de la serie de Taylor para las funciones coseno y seno:

\cos a=1-{\frac {a^{2}}{2}}+O\left(a^{4}\right),\,\operatorname {sen} a=a+O\left(a^{3}\right)

Sustituyendo estas expresiones en la ley esférica de los cosenos se obtiene:

1-{\frac {c^{2}}{2}}+O\left(c^{4}\right)=1-{\frac {a^{2}}{2}}-{\frac {b^{2}}{2}}+{\frac {a^{2}b^{2}}{4}}+O\left(a^{4}\right)+O\left(b^{4}\right)+\cos(C)\left(ab+O\left(a^{3}b\right)+O\left(ab^{3}\right)+O\left(a^{3}b^{3}\right)\right)

o después de simplificar:

c^{2}=a^{2}+b^{2}-2ab\cos C+O\left(c^{4}\right)+O\left(a^{4}\right)+O\left(b^{4}\right)+O\left(a^{2}b^{2}\right)+O\left(a^{3}b\right)+O\left(ab^{3}\right)+O\left(a^{3}b^{3}\right).

Los términos cota superior O para $a$ y $b$ están dominados por $O (a 4) + O (b 4)$ a medida que $a$ y $b$ se vuelven pequeños, por lo que se puede escribir esta última expresión como:

c^{2}=a^{2}+b^{2}-2ab\cos C+O\left(a^{4}\right)+O\left(b^{4}\right)+O\left(c^{4}\right).

Véase también[editar]

Referencias[editar]

↑ ^a ^b ^c W. Gellert, S. Gottwald, M. Hellwich, H. Kästner, and H. Küstner, The VNR Concise Encyclopedia of Mathematics, 2nd ed., ch. 12 (Van Nostrand Reinhold: New York, 1989).
↑ Romuald Ireneus 'Scibor-Marchocki, Spherical trigonometry, Elementary-Geometry Trigonometry web page (1997).
↑ R. W. Sinnott, "Virtues of the Haversine", Sky and Telescope 68 (2), 159 (1984).
↑ Reiman, István (1999). Geometria és határterületei. Szalay Könyvkiadó és Kereskedőház Kft. p. 83.

Datos: Q2996944

[VNR-1] W. Gellert, S. Gottwald, M. Hellwich, H. Kästner, and H. Küstner, The VNR Concise Encyclopedia of Mathematics, 2nd ed., ch. 12 (Van Nostrand Reinhold: New York, 1989).

[Ireneus-2] Romuald Ireneus 'Scibor-Marchocki, Spherical trigonometry, Elementary-Geometry Trigonometry web page (1997).

[3] R. W. Sinnott, "Virtues of the Haversine", Sky and Telescope 68 (2), 159 (1984).

[4] Reiman, István (1999). Geometria és határterületei. Szalay Könyvkiadó és Kereskedőház Kft. p. 83.

[1]

[2]

[3]

[4]