Gráfico de flujo de señal
Un gráfico de flujo de señal ( SFG ), inventado por Claude Shannon,[1] pero a menudo llamado gráfico de Mason en honor a Samuel Jefferson Mason quien acuñó el término,[2] es un diagrama de flujo especializado, un grafo dirigido en el cual los nodos representan variables del sistema y las ramas (aristas, arcos o flechas) representan conexiones funcionales entre pares de nodos. Por lo tanto, la teoría de los gráficos de flujo de señales se basa en la de los gráficos dirigidos (también llamados dígrafos), que incluye también la de los gráficos orientados. Esta teoría matemática de los dígrafos existe, por supuesto, bastante aparte de sus aplicaciones.[3][4]
Los SFG se usan más comúnmente para representar el flujo de señal en un sistema físico y su(s) controlador(es), formando un sistema ciberfísico. Entre sus otros usos está la representación del flujo de señal en varias redes electrónicas y amplificadores, filtros digitales, filtros de estado variable y algunos otros tipos de filtros analógicos. En casi toda la literatura, un gráfico de flujo de señal está asociado con un conjunto de ecuaciones lineales.
Historia[editar]
Wai-Kai Chen escribió: "El concepto de un gráfico de flujo de señal fue originalmente desarrollado por Shannon [1942][1] al tratar con computadoras analógicas. El mayor crédito para la formulación de gráficos de flujo de señal normalmente se extiende a Mason [1953],[2] [1956].[5] Mostró cómo usar la técnica de gráfico de flujo de señal para resolver algunos problemas electrónicos difíciles de una manera relativamente simple. El término gráfico de flujo de señal se usó debido a su aplicación original a problemas electrónicos y la asociación con señales electrónicas y diagramas de flujo de los sistemas en estudio ".[6]
Lorens escribió: "Anterior al trabajo de Mason , CE Shannon[1] desarrolló una serie de propiedades de lo que ahora se conoce como gráficos de flujo. Desafortunadamente, el paper originalmente tenía una clasificación restringida y muy pocas personas tenían acceso al material ".[7]
"Las reglas para la evaluación de la gráfica determinante de una Mason Graph fueron dadas y probadas por Shannon [1942] utilizando inducción matemática. Su obra permaneció esencialmente desconocida incluso después de que Mason publicara su obra clásica en 1953. Tres años más tarde, Mason [1956] redescubrió las reglas y las probó considerando el valor de un determinante y cómo cambia a medida que las variables se agregan a la gráfica. [...] " [8]
Dominio de aplicación[editar]
Robichaud et al. identifique el dominio de aplicación de los SFG de la siguiente manera:[9]
- "Todos los sistemas físicos análogos a estas redes [construidos con transformadores ideales, elementos activos y giradores] constituyen el dominio de aplicación de las técnicas desarrolladas [aquí]. Trent[10] ha demostrado que todos los sistemas físicos que satisfacen las siguientes condiciones entran en esta categoría.
- El sistema concentrado finito está compuesto por varias partes simples, cada una de las cuales tiene propiedades dinámicas conocidas que pueden definirse mediante ecuaciones que utilizan dos tipos de variables escalares y parámetros del sistema. Las variables del primer tipo representan cantidades que pueden medirse, al menos conceptualmente, al unir un instrumento indicador a dos puntos de conexión del elemento. Las variables del segundo tipo caracterizan cantidades que pueden medirse conectando un medidor en serie con el elemento. Las velocidades y posiciones relativas, los diferenciales de presión y los voltajes son cantidades típicas de la primera clase, mientras que las corrientes eléctricas, las fuerzas y las tasas de flujo de calor son variables del segundo tipo. Firestone ha sido el primero en distinguir estos dos tipos de variables con los nombres de las variables y las variables .
- Las variables del primer tipo deben obedecer a una ley de malla, análoga a la ley de voltaje de Kirchhoff, mientras que las variables del segundo tipo deben satisfacer una ley de incidencia análoga a la ley actual de Kirchhoff.
- Las dimensiones físicas de los productos apropiados de las variables de los dos tipos deben ser consistentes. Para los sistemas en los que se satisfacen estas condiciones, es posible dibujar un gráfico lineal isomorfo con las propiedades dinámicas del sistema según lo descrito por las variables elegidas. Las técnicas [...] se pueden aplicar directamente a estos gráficos lineales, así como a las redes eléctricas, para obtener un gráfico de flujo de señal del sistema ".
Conceptos básicos del diagrama de flujo[editar]
Mason introdujo la siguiente ilustración y su significado para ilustrar conceptos básicos:[2]

En los diagramas de flujo simples de la figura, la dependencia funcional de un nodo se indica mediante una flecha entrante, el nodo que origina esta influencia es el comienzo de esta flecha y, en su forma más general, el gráfico de flujo de señal indica mediante flechas entrantes solo aquellos nodos que influyen en el procesamiento en el nodo receptor, y en cada nodo, i , las variables entrantes se procesan de acuerdo con una función asociada con ese nodo, digamos Fi. El diagrama de flujo en (a) representa un conjunto de relaciones explícitas:
El nodo x1 es un nodo aislado porque no hay flechas entrantes; las ecuaciones para x2 y x3 tienen las gráficas que se muestran en las partes (b) y (c) de la figura.
Estas relaciones definen para cada nodo una función que procesa las señales de entrada que recibe. Cada nodo no fuente combina las señales de entrada de alguna manera y transmite una señal resultante a lo largo de cada rama saliente. "Un gráfico de flujo, como lo definió originalmente Mason, implica un conjunto de relaciones funcionales, lineales o no".[9]
Sin embargo, el gráfico de Mason que se usa comúnmente es más restringido, asumiendo que cada nodo simplemente suma sus flechas entrantes y que cada rama involucra solo al nodo iniciador involucrado. Por lo tanto, en este enfoque más restrictivo, el nodo x 1 no se ve afectado mientras:
y ahora las funciones fij pueden asociarse con las ramas de flujo de señal ij uniendo el par de nodos xi, xj, en lugar de tener relaciones generales asociadas con cada nodo. Una contribución de un nodo a sí mismo como f33 para x3 se llama un auto-bucle. Con frecuencia, estas funciones son simplemente factores multiplicativos (a menudo llamados transmitancias o ganancias ), por ejemplo, fij (xj) = cij xj , donde c es un escalar, pero posiblemente una función de algún parámetro como la variable de transformación de Laplace s. Los gráficos de flujo de señal se usan muy a menudo con señales transformadas con Laplace, y en este caso la transmitancia, c(s), a menudo se denomina función de transferencia.
Escogiendo las variables[editar]
En general, hay varias formas de elegir las variables en un sistema complejo. De acuerdo con cada elección, se puede escribir un sistema de ecuaciones y cada sistema de ecuaciones se puede representar en una gráfica. Esta formulación de las ecuaciones se vuelve directa y automática si uno tiene a su disposición técnicas que permiten dibujar una gráfica directamente desde el diagrama esquemático del sistema en estudio. La estructura de los gráficos así obtenidos se relaciona de manera simple con la topología del diagrama esquemático, y se hace innecesario considerar las ecuaciones, incluso implícitamente, para obtener el gráfico. En algunos casos, uno simplemente tiene que imaginar el diagrama de flujo en el diagrama esquemático y las respuestas deseadas se pueden obtener sin siquiera dibujar el diagrama de flujo.Robichaud[11]
No singularidad[editar]
Robichaud et al. escribió: "El gráfico de flujo de señal contiene la misma información que las ecuaciones de las que se deriva; pero no existe una correspondencia uno a uno entre el gráfico y el sistema de ecuaciones. Un sistema dará diferentes gráficos según el orden en que se usan las ecuaciones para definir la variable escrita en el lado izquierdo." [9] Si todas las ecuaciones relacionan todas las variables dependientes, entonces hay n! posibles SFGs para elegir.[12]
Gráficos de flujo de señal lineales[editar]
Los métodos de gráfico de flujo de señal lineal solo se aplican a sistemas invariantes en el tiempo lineal, según lo estudiado por su teoría asociada. Cuando se modela un sistema de interés, el primer paso a menudo es determinar las ecuaciones que representan la operación del sistema sin asignar causas y efectos (esto se denomina modelado acausal).[13] Un SFG se deriva entonces de este sistema de ecuaciones.
Un SFG lineal consiste en nodos indicados por puntos y ramas direccionales ponderadas indicadas por flechas. Los nodos son las variables de las ecuaciones y los pesos de rama son los coeficientes. Las señales solo pueden atravesar una rama en la dirección indicada por su flecha. Los elementos de un SFG solo pueden representar las operaciones de multiplicación por un coeficiente y una suma, que son suficientes para representar las ecuaciones restringidas. Cuando una señal atraviesa una rama en la dirección indicada, la señal se multiplica por el peso de la rama. Cuando dos o más ramas se dirigen al mismo nodo, se agregan sus salidas.
Para los sistemas descritos por ecuaciones lineales algebraicas o diferenciales, el gráfico de señal-flujo es matemáticamente equivalente al sistema de ecuaciones que describen el sistema, y las ecuaciones que gobiernan los nodos se descubren para cada nodo sumando las ramas entrantes a ese nodo. Estas ramas entrantes transmiten las contribuciones de los otros nodos, expresadas como el valor del nodo conectado multiplicado por el peso de la rama de conexión, generalmente un número real o función de algún parámetro (por ejemplo, una variable de transformación de Laplace s).
Para las redes lineales activas, Choma escribe:[14] "Por una 'representación de flujo de señal' [o 'gráfico', como se conoce comúnmente] nos referimos a un diagrama que, al mostrar las relaciones algebraicas entre las variables de red relevantes, dibuja una imagen inequívoca de la forma en que una señal de entrada aplicada 'fluye' de entrada a salida ... puertos".
Chen describe una motivación para un análisis de SFG:[15]
- "El análisis de un sistema lineal se reduce en última instancia a la solución de un sistema de ecuaciones algebraicas lineales. Como alternativa a los métodos algebraicos convencionales para resolver el sistema, es posible obtener una solución considerando las propiedades de ciertos gráficos dirigidos asociados con el sistema. Las incógnitas de las ecuaciones corresponden a los nodos de la gráfica, mientras que las relaciones lineales entre ellas aparecen en forma de bordes dirigidos que conectan los nodos. ...Los gráficos dirigidos asociados en muchos casos se pueden configurar directamente mediante la inspección del sistema físico sin la necesidad de formular primero las ecuaciones asociadas..."
Componentes básicos[editar]

Un gráfico de flujo de señal lineal está relacionado con un sistema de ecuaciones lineales[16] de la siguiente forma:
-
- donde = transmitancia (o ganancia) de a .
La figura de la derecha muestra varios elementos y construcciones de un gráfico de flujo de señal (SFG).[17]
- La exposición (a) es un nodo. En este caso, el nodo está etiquetado . Un nodo es un vértice que representa una variable o señal.
- Un nodo de origen solo tiene ramas salientes (representa una variable independiente). Como un caso especial, un nodo de entrada se caracteriza por tener una o más flechas adjuntas apuntando hacia afuera del nodo y ninguna flecha apuntando hacia el nodo. Cualquier SFG abierto y completo tendrá al menos un nodo de entrada.
- Un nodo de salida o receptor solo tiene ramas entrantes (representa una variable dependiente). Aunque cualquier nodo puede ser una salida, los nodos de salida explícitos se usan a menudo para proporcionar claridad. Los nodos de salida explícitos se caracterizan por tener una o más flechas adjuntas apuntando hacia el nodo y ninguna flecha apuntando hacia afuera del nodo. No se requieren nodos de salida explícitos.
- Un nodo mixto tiene ramas entrantes y salientes.
- El Anexo (b) es una rama con una ganancia multiplicativa de . El significado es que la salida, en la punta de la flecha, es veces la entrada en la cola de la flecha. La ganancia puede ser una constante simple o una función (por ejemplo: una función de alguna variable de transformación, como , o , para las relaciones de transformación de Laplace, Fourier o Z).
- El Anexo (c) es una rama con una ganancia multiplicativa de uno. Cuando se omite la ganancia, se asume que es la unidad.
- Exhibición (d) se multiplica por la ganancia .
- Exhibición (e) es un nodo de salida explícito; el borde entrante tiene una ganancia de .
- El Anexo (f) representa la suma. Cuando dos o más flechas apuntan a un nodo, se agregan las señales transportadas por los bordes.
- El objeto expuesto (g) representa un bucle simple. La ganancia de bucle es .
- Exposición (h) representa la expresión .
Los términos utilizados en la teoría SFG lineal también incluyen:[17]
- Camino. Un camino es un conjunto continuo de ramas atravesadas en la dirección indicada por las flechas de rama.
- Camino abierto Si no se vuelve a visitar ningún nodo, la ruta está abierta.
- Sendero hacia adelante. Una ruta desde un nodo de entrada (fuente) a un nodo de salida (sumidero) que no vuelve a visitar ningún nodo.
- Ganancia de ruta: el producto de las ganancias de todas las ramas en la ruta.
- Lazo. Un camino cerrado. (se origina y termina en el mismo nodo, y ningún nodo se toca más de una vez).
- Ganancia de bucle : el producto de las ganancias de todas las ramas en el bucle.
- Bucles no tocantes. Los bucles no tocantes no tienen nodos comunes.
- Reducción del gráfico. Eliminación de uno o más nodos de un gráfico utilizando transformaciones de gráfico.
- Nodo residual. En cualquier proceso contemplado de reducción de gráficos, los nodos que se retendrán en el nuevo gráfico se denominan nodos residuales.[2]
- La división de un nodo. La división de un nodo corresponde a la división de un nodo en dos medios nodos, uno es un sumidero y el otro una fuente.[18]
- Índice : el índice de un gráfico es el número mínimo de nodos que deben dividirse para eliminar todos los bucles de un gráfico.
- Nodo de índice Los nodos que se dividen para determinar el índice de un gráfico se denominan nodos de índice y, en general, no son únicos.
Reducción sistemática a fuentes y sumideros[editar]
Un gráfico de flujo de señal puede simplificarse mediante reglas de transformación de gráfico.[19][20][21] Estas reglas de simplificación también se conocen como álgebra de gráficos de flujo de señal.[21] El propósito de esta reducción es relacionar las variables de interés dependientes (nodos residuales, sumideros) con sus variables independientes (fuentes).
La reducción sistemática de un gráfico de señal-flujo lineal es un método gráfico equivalente al método de eliminación de Gauss-Jordan para resolver ecuaciones lineales.[22]
Las reglas que se presentan a continuación pueden aplicarse una y otra vez hasta que el gráfico de flujo de señal se reduzca a su "forma residual mínima". Una reducción adicional puede requerir la eliminación del bucle o el uso de una "fórmula de reducción" con el objetivo de conectar directamente los nodos sumideros que representan las variables dependientes a los nodos de origen que representan las variables independientes. De esta manera, cualquier gráfico de flujo de señal se puede simplificar eliminando sucesivamente los nodos internos hasta que solo queden los nodos de entrada y salida y de índice.[23][24] Robichaud describió este proceso de reducción sistemática del diagrama de flujo:
Para reducir digitalmente un gráfico de flujo utilizando un algoritmo, Robichaud extiende la noción de un gráfico de flujo simple a un gráfico de flujo generalizado :
La definición de una transformación elemental varía de un autor a otro:
- Algunos autores solo consideran como transformaciones elementales la suma de las ganancias de borde paralelo y la multiplicación de las ganancias de borde de serie, pero no la eliminación de los bucles automáticos[22][25]
- Otros autores consideran la eliminación de un self-loop como una transformación elemental[26]
Bordes paralelos. Reemplace los bordes paralelos con un solo borde que tenga una ganancia igual a la suma de las ganancias originales.
La gráfica de la izquierda tiene bordes paralelos entre nodos. A la derecha, estos bordes paralelos se han reemplazado con un solo borde que tiene una ganancia igual a la suma de las ganancias en cada borde original.
Las ecuaciones correspondientes a la reducción entre N y nodo I 1 son:
Bordes de salida. Reemplace los bordes de salida con los bordes que fluyen directamente de las fuentes del nodo.
El gráfico de la izquierda tiene un nodo intermedio N entre los nodos de los que tiene entradas y los nodos a los que fluye. El gráfico de la derecha muestra los flujos directos entre estos conjuntos de nodos, sin transitar a través de N. En aras de la simplicidad, N y sus entradas no están representadas. Las salidas de N se eliminan.
Las ecuaciones correspondientes a la reducción que relaciona directamente las señales de entrada de N con sus señales de salida son:
Nodos de señal cero
Elimine los bordes de salida de un nodo determinado para tener un valor de cero.
Si el valor de un nodo es cero, sus bordes de salida pueden eliminarse.
Nodos sin salidas
Eliminar un nodo sin salidas.
En este caso, N no es una variable de interés y no tiene bordes salientes; por lo tanto, N , y sus bordes de entrada, pueden ser eliminados. Borde auto-bucle. Reemplace los bordes de bucle ajustando las ganancias en los bordes entrantes.
 El gráfico de la izquierda tiene un borde de bucle en el nodo N , con una ganancia de g . A la derecha, el borde de bucle se ha eliminado, y todos los bordes de entrada tienen su ganancia dividida por (1-g) .
El gráfico de la izquierda tiene un borde de bucle en el nodo N , con una ganancia de g . A la derecha, el borde de bucle se ha eliminado, y todos los bordes de entrada tienen su ganancia dividida por (1-g) .
Las ecuaciones correspondientes a la reducción entre N y todas sus señales de entrada son:
Implementaciones[editar]
El procedimiento anterior para construir el SFG a partir de un sistema de ecuaciones de acausal y para resolver las ganancias del SFG se ha implementado[27] como un complemento a MATHLAB 68,[28] un sistema en línea que proporciona ayuda de la máquina para los procesos simbólicos mecánicos Encontrado en el análisis .
Resolviendo ecuaciones lineales[editar]
Los gráficos de flujo de señal se pueden usar para resolver conjuntos de ecuaciones lineales simultáneas.[29] El conjunto de ecuaciones debe ser consistente y todas las ecuaciones deben ser linealmente independientes.
Poniendo las ecuaciones en "forma estándar"[editar]

Para M ecuaciones con N incógnitas donde cada y j es un valor conocido y cada x j es un valor desconocido, hay una ecuación para cada conocido de la siguiente forma.
- ;la forma usual para ecuaciones lineales simultáneas con 1 ≤ j ≤ M
Aunque es factible, particularmente para casos simples, establecer un gráfico de flujo de señal usando las ecuaciones en esta forma, algunas reorganizaciones permiten un procedimiento general que funciona fácilmente para cualquier conjunto de ecuaciones, como se presenta ahora. Para proceder, primero se reescriben las ecuaciones como
y reescrito como
y finalmente reescrito como
- ; forma adecuada para expresarse como un gráfico de flujo de señal.
- donde δ kj = delta de Kronecker
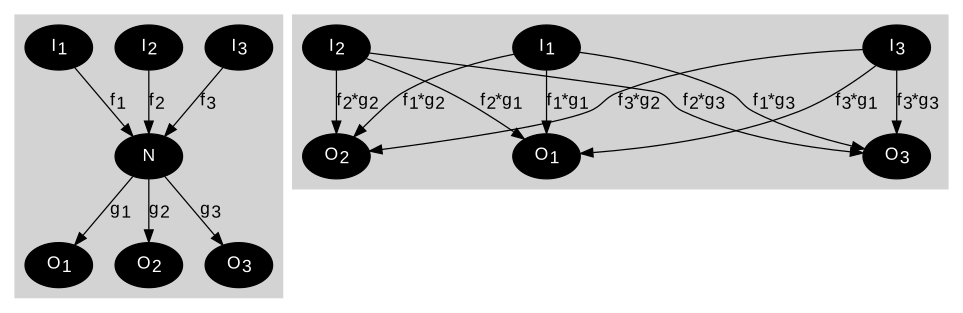
El gráfico de flujo de señal ahora se organiza seleccionando una de estas ecuaciones y dirigiéndose al nodo en el lado derecho. Este es el nodo por el cual el nodo se conecta a sí mismo con la rama de peso que incluye un '+1', haciendo un bucle automático en el gráfico de flujo. Los otros términos en esa ecuación conectan este nodo primero a la fuente en esta ecuación y luego a todas las otras ramas que inciden en este nodo. Cada ecuación se trata de esta manera, y luego cada rama incidente se une a su nodo emanante respectivo. Por ejemplo, el caso de tres variables se muestra en la figura, y la primera ecuación es:
donde el lado derecho de esta ecuación es la suma de las flechas ponderadas que inciden en el nodo x 1 .
Como hay una simetría básica en el tratamiento de cada nodo, un punto de partida simple es una disposición de nodos con cada nodo en un vértice de un polígono regular. Cuando se expresa utilizando los coeficientes generales { c in }, el entorno de cada nodo es, como todo lo demás, aparte de una permutación de índices. Tal implementación para un conjunto de tres ecuaciones simultáneas se ve en la figura.[30]
A menudo, los valores conocidos, yj se toman como las causas primarias y los valores desconocidos, x j son efectos, pero independientemente de esta interpretación, la última forma para el conjunto de ecuaciones se puede representar como un gráfico de flujo de señal.
Aplicando la fórmula de ganancia de Mason.[editar]
En el caso más general, los valores para todas las variables x k pueden calcularse calculando la fórmula de ganancia de Mason para la ruta de cada y j a cada x k y usando la superposición.
- donde Gkj = la suma de la fórmula de ganancia de Mason calculada para todas las rutas desde la entrada y j hasta la variable x k .
En general, hay rutas N-1 desde y j hasta la variable x k, por lo que el esfuerzo computacional para calcular G kj es proporcional a N-1. Como hay M valores de y j , G kj debe calcularse M veces para un solo valor de x k . El esfuerzo computacional para calcular una sola variable x k es proporcional a (N-1) (M). El esfuerzo por calcular todas las variables x k es proporcional a (N) (N-1) (M). Si hay N ecuaciones y N incógnitas, entonces el esfuerzo de cálculo es del orden de N 3 .
Relación con diagramas de bloques[editar]

Para algunos autores, un gráfico de señal-flujo lineal está más restringido que un diagrama de bloques ,[31] en que el SFG describe rigurosamente las ecuaciones algebraicas lineales representadas por un gráfico dirigido.
Para otros autores, los diagramas de bloques lineales y los gráficos de flujo de señal lineales son formas equivalentes de representar un sistema, y cualquiera de ellos puede usarse para resolver la ganancia.[32]
Bakshi & Bakshi proporciona una tabulación de la comparación entre diagramas de bloques y gráficos de flujo de señal,[33] y otra tabulación de Kumar.[34] Según Barker et al. :[35]
- "El gráfico de flujo de señal es el método más conveniente para representar un sistema dinámico. La topología del gráfico es compacta y las reglas para manipularla son más fáciles de programar que las reglas correspondientes que se aplican a los diagramas de bloques ".
En la figura, se muestra un diagrama de bloques simple para un sistema de retroalimentación con dos interpretaciones posibles como un gráfico de flujo de señal. La entrada R (s) es la señal de entrada transformada con Laplace; se muestra como un nodo fuente en el gráfico de flujo de señal (un nodo fuente no tiene bordes de entrada). La señal de salida C (s) es la variable de salida transformada con Laplace. Se representa como un nodo sumidero en el diagrama de flujo (un sumidero no tiene bordes de salida). G (s) y H (s) son funciones de transferencia, con H (s) que sirven para realimentar una versión modificada de la salida a la entrada, B (s) . Las dos representaciones del diagrama de flujo son equivalentes.
Interpretando la 'causalidad'[editar]
El término "causa y efecto" fue aplicado por Mason a los SFG:[2]
- "El proceso de construcción de una gráfica consiste en rastrear una sucesión de causas y efectos a través del sistema físico. Una variable se expresa como un efecto explícito debido a ciertas causas; a su vez, son reconocidos como efectos debido a otras causas ".
- - SJ Mason: Sección IV: Aplicaciones ilustrativas de la técnica del diagrama de flujo.
y ha sido repetido por muchos autores posteriores:[36]
- "El gráfico de flujo de señal es otra herramienta visual para representar relaciones causales entre componentes del sistema. Es una versión simplificada de un diagrama de bloques introducido por SJ Mason como una representación de causa y efecto de sistemas lineales ".
- - Arthur GO Mutambara: Diseño y análisis de sistemas de control , p.238
Sin embargo, el artículo de Mason se preocupa por mostrar con gran detalle cómo un conjunto de ecuaciones está conectado a un SFG, un énfasis no relacionado con las nociones intuitivas de "causa y efecto". Las intuiciones pueden ser útiles para llegar a un SFG o para obtener información de un SFG, pero no son esenciales para el SFG. La conexión esencial del SFG es a su propio conjunto de ecuaciones, como lo describe, por ejemplo, Ogata:[37]
- "Un gráfico de flujo de señal es un diagrama que representa un conjunto de ecuaciones algebraicas simultáneas. Al aplicar el método del gráfico de flujo de señal al análisis de sistemas de control, primero debemos transformar las ecuaciones diferenciales lineales en ecuaciones algebraicas en [la variable de la transformada de Laplace ] s . . "
- - Katsuhiko Ogata: Ingeniería de Control Moderna , p. 104
No hay referencia a "causa y efecto" aquí, y como dijo Barutsky:[38]
- "Al igual que los diagramas de bloques, los gráficos de flujo de señales representan la estructura computacional, no la física de un sistema".
- - Wolfgang Borutzky, Metodología de la Gráfica de Bonos , p. 10
El término "causa y efecto" puede malinterpretarse cuando se aplica al SFG, y puede interpretarse incorrectamente para sugerir una visión del sistema de la causalidad,[39] lugar de un significado computacional . Para mantener la discusión clara, puede ser recomendable utilizar el término "causalidad computacional", como se sugiere para los gráficos de enlace :[40]
- "La literatura de Bond-graph utiliza el término causalidad computacional, que indica el orden de cálculo en una simulación, para evitar cualquier interpretación en el sentido de causalidad intuitiva".
El término "causalidad computacional" se explica utilizando el ejemplo de corriente y voltaje en una resistencia:[41]
- "La causalidad computacional de las leyes físicas no puede, por lo tanto, estar predeterminada, sino que depende del uso particular de esa ley. No podemos concluir si es la corriente que fluye a través de una resistencia la que causa una caída de voltaje, o si es la diferencia de potenciales en los dos extremos de la resistencia lo que hace que la corriente fluya. Físicamente, estos son simplemente dos aspectos concurrentes de un mismo fenómeno físico. Desde el punto de vista informático, es posible que tengamos que asumir, en ocasiones, una posición y otras veces la otra ".
- - François Cellier & Ernesto Kofman: §1.5 Software de simulación hoy y mañana , p. 15
Se puede organizar un programa o algoritmo de computadora para resolver un conjunto de ecuaciones usando varias estrategias. Difieren en cómo priorizan la búsqueda de algunas de las variables en términos de las otras, y estas decisiones algorítmicas, que son simplemente acerca de la estrategia de la solución, luego configuran las variables expresadas como variables dependientes anteriormente en la solución como "efectos", determinadas por las variables restantes que ahora son "causas", en el sentido de "causalidad computacional".
Usando esta terminología, es la causalidad computacional , no la causalidad del sistema , lo que es relevante para el SFG. Existe un amplio debate filosófico, no relacionado específicamente con el SFG, sobre las conexiones entre la causalidad computacional y la causalidad del sistema.[42]
Gráficos de flujo de señales para análisis y diseño[editar]
Los gráficos de flujo de señal se pueden usar para el análisis, es decir, para comprender un modelo de un sistema existente, o para la síntesis, para determinar las propiedades de una alternativa de diseño.
Gráficos de flujo de señales para análisis de sistemas dinámicos.[editar]
Al construir un modelo de un sistema dinámico, Dorf & Bishop proporciona una lista de pasos:[43]
- Definir el sistema y sus componentes.
- Formular el modelo matemático y enumerar los supuestos necesarios.
- Escribe las ecuaciones diferenciales que describen el modelo.
- Resuelve las ecuaciones para las variables de salida deseadas.
- Examinar las soluciones y los supuestos.
- Si es necesario, vuelva a analizar o rediseñar el sistema.
- —RC Dorf y RH Bishop, Modern Control Systems , Capítulo 2, pág. 2
En este flujo de trabajo, las ecuaciones del modelo matemático del sistema físico se utilizan para derivar las ecuaciones del gráfico de señal-flujo.
Gráficos de flujo de señal para síntesis de diseño[editar]
Los gráficos de flujo de señal se han utilizado en Design Space Exploration (DSE) , como una representación intermedia hacia una implementación física. El proceso DSE busca una solución adecuada entre diferentes alternativas. En contraste con el flujo de trabajo de análisis típico, donde un sistema de interés se modela primero con las ecuaciones físicas de sus componentes, la especificación para sintetizar un diseño podría ser una función de transferencia deseada. Por ejemplo, diferentes estrategias crearían diferentes gráficos de flujo de señal, de los cuales se derivan las implementaciones.[44] Otro ejemplo utiliza un SFG anotado como una expresión del comportamiento en tiempo continuo, como entrada a un generador de arquitectura[45]
Fórmulas de Shannon y Shannon-Happ.[editar]
La fórmula de Shannon es una expresión analítica para calcular la ganancia de un conjunto interconectado de amplificadores en una computadora analógica. Durante la Segunda Guerra Mundial, mientras investigaba el funcionamiento funcional de una computadora analógica, Claude Shannon desarrolló su fórmula. Debido a las restricciones de tiempo de guerra, el trabajo de Shannon no se publicó en ese momento y, en 1952, Mason redescubrió la misma fórmula.
Happ generalizó la fórmula de Shannon para sistemas topológicamente cerrados.[46] La fórmula de Shannon-Happ se puede utilizar para derivar funciones de transferencia, sensibilidades y funciones de error.[47]
Para un conjunto consistente de relaciones unilaterales lineales, la fórmula de Shannon-Happ expresa la solución mediante sustitución directa (no iterativa).[47][48]
El software de circuito eléctrico NASAP de la NASA se basa en la fórmula de Shannon-Happ.[47][48]
Ejemplos de gráficos de flujo de señal lineal[editar]
Amplificador de voltaje simple[editar]
La amplificación de una señal V 1 por un amplificador con ganancia a 12 se describe matemáticamente por
Esta relación representada por el gráfico de señal-flujo de la Figura 1 es que V 2 depende de V 1, pero no implica dependencia de V 1 en V 2 . Ver la página 57 de Kou.[49]
Amplificador de realimentación negativa ideal[editar]
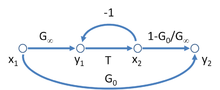

Un posible SFG para el modelo de ganancia asintótica para un amplificador de retroalimentación negativa se muestra en la Figura 3, y conduce a la ecuación para la ganancia de este amplificador como
La interpretación de los parámetros es la siguiente: T = relación de retorno , G ∞ = ganancia directa del amplificador, G 0 = feedforward (que indica la posible naturaleza bilateral de la retroalimentación, posiblemente deliberada como en el caso de la compensación de feedforward). La Figura 3 tiene el aspecto interesante que se asemeja a la Figura 2 para la red de dos puertos con la adición de la relación de retroalimentación adicional x 2 = T y 1 .
A partir de esta expresión de ganancia, es evidente una interpretación de los parámetros G 0 y G ∞ , a saber:
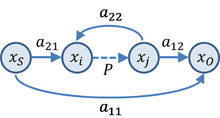
Hay muchos SFG posibles asociados con cualquier relación de ganancia particular. La Figura 4 muestra otro SFG para el modelo de ganancia asintótica que puede ser más fácil de interpretar en términos de un circuito. En este gráfico, el parámetro β se interpreta como un factor de realimentación y A como un "parámetro de control", posiblemente relacionado con una fuente dependiente en el circuito. Usando este gráfico, la ganancia es
Para conectarse al modelo de ganancia asintótica, los parámetros A y β no pueden ser parámetros de circuito arbitrarios, sino que deben relacionarse con la relación de retorno T mediante:
y a la ganancia asintótica como:
Sustituyendo estos resultados en la expresión de ganancia,
Cuál es la fórmula del modelo de ganancia asintótica.
Circuito eléctrico que contiene una red de dos puertos[editar]

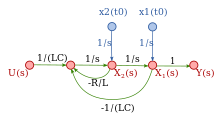
La figura de la derecha muestra un circuito que contiene una red de dos puertos de parámetro y . V in es la entrada del circuito y V 2 es la salida. Las ecuaciones de dos puertos imponen un conjunto de restricciones lineales entre los voltajes y corrientes de sus puertos. Las ecuaciones terminales imponen otras restricciones. Todas estas restricciones están representadas en el SFG (Signal Flow Graph) debajo del circuito. Solo hay una ruta de entrada a salida que se muestra en un color diferente y tiene una ganancia (de voltaje) de -R L y 21 . También hay tres bucles: -R en y 11 , -R L y 22 , R en y 21 R L y 12 . A veces, un bucle indica retroalimentación intencional pero también puede indicar una restricción en la relación de dos variables. Por ejemplo, la ecuación que describe una resistencia dice que la relación del voltaje a través de la resistencia a la corriente a través de la resistencia es una constante que se llama resistencia. Esto puede interpretarse como el voltaje es la entrada y la corriente es la salida, o la corriente es la entrada y el voltaje es la salida, o simplemente que el voltaje y la corriente tienen una relación lineal. Prácticamente todos los dos dispositivos terminales pasivos en un circuito se mostrarán en el SFG como un bucle.
El SFG y el esquema representan el mismo circuito, pero el esquema también sugiere el propósito del circuito. En comparación con el esquema, el SFG es incómodo, pero tiene la ventaja de que la ganancia de la entrada a la salida se puede escribir mediante inspección utilizando la regla de Mason .
Mecatrónica: Posicionar el servo con retroalimentación multi-loop[editar]

Este ejemplo es representativo de un SFG (gráfico de flujo de señal) utilizado para representar un sistema de servocontrol e ilustra varias características de los SFG. Algunos de los bucles (bucle 3, bucle 4 y bucle 5) son bucles de retroalimentación diseñados de forma intencionada y extrínseca. Estos se muestran con líneas de puntos. También hay bucles intrínsecos (bucle 0, bucle1, bucle2) que no son bucles de retroalimentación intencionales, aunque se pueden analizar como si fueran. Estos bucles se muestran con líneas continuas. Los bucles 3 y 4 también se conocen como bucles menores porque están dentro de un bucle más grande.
- El camino hacia adelante comienza con θ C , el comando de posición deseado. Esto se multiplica por K P, que podría ser una constante o una función de la frecuencia. K P incorpora la ganancia de conversión del DAC y cualquier filtrado en la salida del DAC. La salida de K P es el comando de velocidad V ωC que se multiplica por K V, que puede ser una constante o una función de la frecuencia. La salida de K V es el comando actual, V IC que se multiplica por K C, que puede ser una constante o una función de frecuencia. La salida de K C es la tensión de salida del amplificador, V A. La corriente, I M , aunque el devanado del motor es la integral de la tensión aplicada a la inductancia. El motor produce un par, T , proporcional a I M. Los motores de imán permanente tienden a tener una función de corriente lineal a par. La constante de conversión de corriente a par es K M. El par, T , dividido por el momento de inercia de la carga, M, es la aceleración, α , que se integra para proporcionar la velocidad de carga ω que se integra para producir la posición de carga, θ LC .
- La trayectoria de avance del bucle 0 afirma que la aceleración es proporcional al par y la velocidad es la integral de tiempo de la aceleración. La ruta hacia atrás dice que a medida que aumenta la velocidad, existe una fricción o un arrastre que contrarresta el par. El torque en la carga disminuye proporcionalmente a la velocidad de la carga hasta que se alcanza el punto en que se usa todo el torque para superar la fricción y la aceleración cae a cero. El bucle 0 es intrínseco.
- El bucle 1 representa la interacción de la corriente de un inductor con sus resistencias internas y externas en serie. La corriente a través de una inductancia es la integral de tiempo del voltaje a través de la inductancia. Cuando se aplica un voltaje por primera vez, todo aparece a través del inductor. Esto se muestra por el camino a través de . A medida que aumenta la corriente, el voltaje cae a través de la resistencia interna del inductor R M y la resistencia externa R S. Esto reduce la tensión a través del inductor y se representa mediante la ruta de realimentación - (RM + RS). La corriente continúa aumentando, pero a una tasa de disminución constante hasta que la corriente alcanza el punto en el que toda la tensión cae (RM + RS). El bucle 1 es intrínseco.
- El bucle 2 expresa el efecto del motor de retroceso EMF. Cada vez que un motor de imán permanente gira, actúa como un generador y produce un voltaje en sus devanados. No importa si la rotación es causada por un par aplicado al eje de transmisión o por la corriente aplicada a los devanados. Esta tensión se conoce como EMF posterior. La ganancia de conversión de la velocidad de rotación hacia atrás EMF es GM. La polaridad del EMF posterior es tal que disminuye la tensión a través de la inductancia del devanado. El bucle 2 es intrínseco.
- El bucle 3 es extrínseco. La corriente en el devanado del motor pasa a través de un detector de sentido. El voltaje, V IM, desarrollado a través del resistor sentido es realimentada al terminal negativo del amplificador de potencia K C. Esta realimentación hace que el amplificador de voltaje actúe como una fuente de corriente controlada por voltaje. Dado que el par del motor es proporcional a la corriente del motor, el subsistema V IC al par de salida actúa como una fuente de par controlada por voltaje. Este subsistema puede denominarse "bucle de corriente" o "bucle de par". El bucle 3 disminuye efectivamente los efectos del bucle 1 y del bucle 2.
- El bucle 4 es extrínseco. Un tacómetro (en realidad un generador de CC de baja potencia) produce una tensión de salida V ωM que es proporcional a la velocidad angular. Esta tensión se alimenta a la entrada negativa de K V. Esta retroalimentación hace que el subsistema de V ωC a la velocidad angular de la carga actúe como una fuente de voltaje a velocidad. Este subsistema puede denominarse "bucle de velocidad". El bucle 4 disminuye efectivamente los efectos del bucle 0 y el bucle 3.
- El bucle 5 es extrínseco. Este es el bucle de realimentación de posición general. La retroalimentación proviene de un codificador de ángulo que produce una salida digital. La posición de salida se resta de la posición deseada por el hardware digital que controla un DAC que controla K P. En el SFG, la ganancia de conversión del DAC se incorpora a K P.
Vea la regla de Mason para el desarrollo de la Fórmula de ganancia de Mason para este ejemplo.
Terminología y clasificación de gráficos de flujo de señales[editar]
Existe cierta confusión en la literatura acerca de qué es un gráfico de flujo de señal; Henry Paynter , inventor de los gráficos de enlace , escribe: "Pero gran parte del declive de los gráficos de flujo de señal [...] se debe en parte a la idea errónea de que las ramas deben ser lineales y los nodos deben ser sumativos. ¡Ni el propio Mason abrazó esta suposición! " [51]
Estándares que cubren los gráficos de flujo de señal.[editar]
- IEEE Std 155-1960, Estándares IEEE en circuitos: Definiciones de términos para gráficos de flujo de señal lineal, 1960.
- Este estándar IEEE define un gráfico de flujo de señal como una red de ramas dirigidas que representan señales dependientes e independientes como nodos . Las ramas entrantes llevan señales de rama a las señales de nodo dependientes. Una señal de nodo dependiente es la suma algebraica de las señales de rama entrantes en ese nodo, es decir, los nodos son sumativos.
Transición de estado del flujo de señal[editar]
Un SFG de transición de estado o diagrama de estado es un diagrama de simulación para un sistema de ecuaciones, que incluye las condiciones iniciales de los estados.[52]
Diagrama de flujo cerrado[editar]

Los diagramas de flujo cerrado describen sistemas cerrados y se han utilizado para proporcionar una base teórica rigurosa para las técnicas topológicas de análisis de circuitos.[46]
- La terminología para la teoría del diagrama de flujo cerrado incluye:
- Nodo contributivo. Punto de suma para dos o más señales entrantes que resultan en una sola señal saliente.
- Nodo distributivo. Punto de muestreo para dos o más señales salientes que resultan de una sola señal entrante.
- Nodo compuesto. Contracción de un nodo contributivo y un nodo distributivo.
- Nodo estrictamente dependiente y estrictamente independiente. Un nodo estrictamente independiente representa una fuente independiente; un nodo estrictamente dependiente representa un medidor.
- Gráficos de flujo abiertos y cerrados. Un diagrama de flujo abierto contiene nodos estrictamente dependientes o estrictamente independientes; De lo contrario, es un diagrama de flujo cerrado.
Gráficos de flujo no lineales[editar]
Mason introdujo tanto gráficos de flujo no lineales como lineales. Para aclarar este punto, escribió Mason: "Un gráfico de flujo lineal es uno cuyas ecuaciones asociadas son lineales".[2]
Ejemplos de funciones de rama no lineales[editar]
Si denotamos con xj la señal en el nodo j , los siguientes son ejemplos de funciones de nodo que no pertenecen a un sistema lineal invariante en el tiempo :
Ejemplos de modelos de gráficos de flujo de señal no lineales[editar]
- Los gráficos de flujo de señal no lineal se pueden encontrar en la literatura de ingeniería eléctrica.[53][54]
- Los gráficos de flujo de señal no lineal también se pueden encontrar en las ciencias de la vida.
Aplicaciones de las técnicas de SFG en diversos campos de la ciencia[editar]
- Circuitos electrónicos
- Caracterización de circuitos secuenciales del tipo Moore y Mealy , obteniendo expresiones regulares de diagramas de estado .[55]
- Síntesis de convertidores de datos no lineales[54]
- Control y teoría de redes.
- Procesamiento de señales estocásticas.[56]
- Fiabilidad de los sistemas electrónicos[57]
- Fisiología y biofísica
- Regulación del gasto cardíaco[58]
- Simulación
- Simulación en ordenadores analógicos[25]
Véase también[editar]
- Modelo de ganancia asintótica
- Gráficos de bonos
- Gráfica de Coates
- Sistemas de control / Diagramas de flujo de señales en el Wikilibro de sistemas de control
- Diagrama de flujo (matemáticas)
- Filtro Leapfrog para un ejemplo de diseño de filtro usando un gráfico de flujo de señal
- Fórmula de ganancia de Mason
- Retroalimentación de bucle menor
- Gráfico de flujo de señal no conmutativo
Notas[editar]
Referencias[editar]
- ↑ a b c CE Shannon (January 1942). The theory and design of linear differential equation machines. Fire Control of the US National Defense Research Committee: Report 411, Section D-2.
- ↑ a b c d e f Mason, Samuel J. (September 1953). «Feedback Theory - Some Properties of Signal Flow Graphs». Proceedings of the IRE 41 (9): 1144-1156. doi:10.1109/jrproc.1953.274449. Archivado desde el original el 19 de febrero de 2018. Consultado el 8 de marzo de 2019. «The flow graph may be interpreted as a signal transmission system in which each node is a tiny repeater station. The station receives signals via the incoming branches, combines the information in some manner, and then transmits the results along each outgoing branch.» Error en la cita: Etiqueta
<ref>no válida; el nombre «Mason» está definido varias veces con contenidos diferentes - ↑ Jørgen Bang-Jensen; Gregory Z. Gutin (2008). Digraphs. Springer. ISBN 9781848009981.
- ↑ Bela Bollobas (1998). Modern graph theory. Springer Science & Business Media. p. 8. ISBN 9781461206194.i
- ↑ SJ Mason (July 1956). «Feedback Theory-Further Properties of Signal Flow Graphs». Proceedings of the IRE 44 (7): 920-926. doi:10.1109/JRPROC.1956.275147. On-line version found at MIT Research Laboratory of Electronics.
- ↑ Chen, Wai-Kai (1976). Applied Graph Theory : Graphs and Electrical Networks. Elsevier. ISBN 9781483164151.(WKC, 1976)
- ↑ Lorens, Charles Stanton (15 de julio de 1956), Vogel, Dan, ed., Technical Report 317 - Theory and applications of flow graphs, Research Laboratory of Electronics, MIT.
- ↑ (WKC, 1976, p. 169)
- ↑ a b c
Louis PA Robichaud; Maurice Boisvert; Jean Robert (1962). «Preface». Signal flow graphs and applications. Prentice Hall. p. x.
Error en la cita: Etiqueta
<ref>no válida; el nombre «Robichaud» está definido varias veces con contenidos diferentes - ↑ Horace M Trent (1955). «Isomorphisms between Oriented Linear Graphs and Lumped Physical Systems». Journal of the Acoustical Society of America 27 (3): 500-527. doi:10.1121/1.1907949.
- ↑ (Robichaud, 1962, p. ix)
- ↑ Narsingh Deo (2004). Graph Theory with Applications to Engineering and Computer Science. PHI Learning Pvt. Ltd. p. 418. ISBN 9788120301450.
- ↑ Kofránek, J; Mateják, M; Privitzer, P; Tribula, M (2008), Causal or acausal modeling: labour for humans or labour for machines, Technical Computing Prague 2008. Conference Proceedings., Prague, p. 16, archivado desde el original el 29 de diciembre de 2009, consultado el 8 de marzo de 2019.
- ↑ J Choma, Jr (April 1990). «Signal flow analysis of feedback networks». IEEE Transactions on Circuits and Systems 37 (4): 455-463. doi:10.1109/31.52748.
- ↑ Wai-Kai Chen (1971). «Chapter 3: Directed graph solutions of linear algebraic equations». Applied graph theory. North-Holland Pub. Co. p. 140. ISBN 978-0444101051.
- ↑ See, for example, Katsuhiko Ogata (2004). «Chapter 3-9: Signal flow graph representation of linear systems». Modern Control Engineering (4th edición). Prentice Hall. pp. 106 ff. ISBN 978-0130609076. However, there is not a one-to-one correspondence: Narsingh Deo (2004). Graph Theory with Applications to Engineering and Computer Science. PHI Learning Pvt. Ltd. p. 418. ISBN 9788120301450.
- ↑ a b Kuo, Benjamin C. (1967). Automatic Control Systems (2nd edición). Prentice-Hall. pp. 59–60.
- ↑ Louis PA Robichaud; Maurice Boisvert; Jean Robert (1962). «§1-4: Definitions and terminology». Signal flow graphs and applications. Prentice Hall. p. 8.
- ↑ J. R. Abrahams; G. P. Coverley (2014). «Chapter 2: Operations with a flow graph». Signal Flow Analysis: The Commonwealth and International Library. Elsevier. pp. 21 ff. ISBN 9781483180700.
- ↑ Isaac M. Horowitz (2013). «Reduction of signal-flow graphs». Synthesis of Feedback Systems. Elsevier. pp. 18 ff. ISBN 9781483267708.
- ↑ a b (Ogata, 2002)
- ↑ a b (Henley, 1973, p. 12)
- ↑ (Phang, 2001)
- ↑ Examples of the signal-flow graph reduction can be found in (Robichaud, 1962)
- ↑ a b (Robichaud, 1962)
- ↑ Fakhfakh, Mourad; Tlelo-Cuautle, Esteban; V. Fernández, Francisco (2012). «Section 4.1.2 Signal flow graphs algebra». En Fakhfakh, ed. Design of Analog Circuits Through Symbolic Analysis. Bentham Science Publishers. p. 418. ISBN 978-1-60805-425-1.
- ↑ Labrèche P., presentación: Circuitos eléctricos lineales: análisis de redes simbólicas , 1977.
- ↑ Carl Engelman, El legado de MATHLAB 68 , publicado en Proceeding SYMSAC '71. Actas del segundo simposio ACM sobre manipulación simbólica y algebraica, páginas 29-41 [1]
- ↑ "... solving a set of simultaneous, linear algebraic equations. This problem, usually solved by matrix methods, can also be solved via graph theory. " Deo, Narsingh (1974). Graph Theory with Applications to Engineering and Computer Science. Prentice-Hall of India. p. 416. ISBN 978-81-203-0145-0. also on-line at [2]
- ↑ Deo, Narsingh (1974). Graph Theory with Applications to Engineering and Computer Science. Prentice-Hall of India. p. 417. ISBN 978-81-203-0145-0. also on-line at [3]
- ↑ "A signal flow graph may be regarded as a simplified version of a block diagram. ... for cause and effect ... of linear systems ...we may regard the signal-flow graphs to be constrained by more rigid mathematical rules, whereas the usage of the block-diagram notation is less stringent." Kuo, Benjamin C. (1991). Automatic Control Systems (6th edición). Prentice-Hall. p. 77. ISBN 978-0-13-051046-4.
- ↑ Gene F. Franklin (Apr 29, 2014). «Appendix W.3 Block Diagram Reduction». Feedback Control of Dynamic Systems. Prentice Hall.
- ↑ V.U.Bakshi U.A.Bakshi (2007). «Table 5.6: Comparison of block diagram and signal flow graph methods». Control Engineering. Technical Publications. p. 120. ISBN 9788184312935.
- ↑ A Anand Kumar (2014). «Table: Comparison of block diagram and signal flow methods». Control Systems (2nd edición). PHI Learning Pvt. Ltd. p. 165. ISBN 9788120349391.
- ↑ HA Barker; M Chen; P. Townsend (2014). «Algorithms for transformations between block diagrams and digital flow graphs». Computer Aided Design in Control Systems 1988: Selected Papers from the 4th IFAC Symposium, Beijing, PRC, 23-25, August 1988. Elsevier. pp. 281 ff.
- ↑ For example, see Arthur G.O. Mutambara (1999). Design and Analysis of Control Systems. CRC Press. p. 238. ISBN 9780849318986.
- ↑ Katsuhiko Ogata (1997). «Signal flow graphs». Modern Control Engineering (4th edición). Prentice Hall. p. 104. ISBN 978-0130432452.
- ↑ Wolfgang Borutzky (2009). Bond Graph Methodology: Development and Analysis of Multidisciplinary Dynamic System Models. Springer Science & Business Media. p. 10. ISBN 9781848828827.
- ↑ James J. Callahan (2000). «Causality: Definition 2.10». The Geometry of Spacetime: An Introduction to Special and General Relativity. Springer Science & Business Media. p. 76. ISBN 9780387986418.
- ↑ John JH Miller; Robert Vichnevetsky (July 22–26, 1991). John JH Miller, ed. IMACS '91, Proceedings of the 13th IMACS World Congress on Computation and Applied Mathematics: July 22-26, 1991, Trinity College, Dublin, Ireland. International Association for Mathematics and Computers in Simulation.
- ↑ François E. Cellier; Ernesto Kofman (2006). Continuous System Simulation. Springer Science & Business Media. p. 15. ISBN 9780387261027.
- ↑ See, for example, Stephan Lewandowsky; Simon Farrell (2010). Computational Modeling in Cognition: Principles and Practice. SAGE Publications. ISBN 9781452236193.
- ↑ Dorf, Richard C.; Bishop, Robert H. (2001). «Chap 2.-1: Introduction». Modern Control Systems. Prentice Hall. p. 2. ISBN 978-0-13-030660-9.
- ↑ Antao, B. A. A.; Brodersen, A.J. (June 1995). «ARCHGEN: Automated synthesis of analog systems». Very Large Scale Integration (VLSI) Systems, IEEE Transactions on 3 (2): 231-244. doi:10.1109/92.386223.
- ↑ Doboli, A.; Dhanwada, N.; Vemuri, R. (May 2000). «A heuristic technique for system-level architecture generation from signal-flow graph representations of analog systems». 2000 IEEE International Symposium on Circuits and Systems. Emerging Technologies for the 21st Century. Proceedings (IEEE Cat No.00CH36353) 3. pp. 181-184. ISBN 978-0-7803-5482-1. doi:10.1109/ISCAS.2000.856026.
- ↑ a b c Happ, William W. (1966). «Flowgraph Techniques for Closed Systems». IEEE Transactions on Aerospace and Electronic Systems. AES-2 (3): 252-264. doi:10.1109/TAES.1966.4501761. Consultado el 27 de enero de 2015.
- ↑ a b c Potash, Hanan; McNamee, Lawrence P. (1968). «Application of unilateral and graph techniques to analysis of linear circuits: Solution by non-iterative methods». Proceedings, ACM National Conference: 367-378. doi:10.1145/800186.810601.
- ↑ a b Okrent, Howard; McNamee, Lawrence P. (1970). «3. 3 Flowgraph Theory». NASAP-70 User's and Programmer's manual. Los Angeles, California: School of Engineering and Applied Science, University of California at Los Angeles. pp. 3-9.
- ↑ Kou (1967)
- ↑ Arnaldo D’Amico, Christian Falconi, Gianluca Giustolisi, Gaetano Palumbo (April 2007). «Resistance of Feedback Amplifiers: A novel representation». IEEE Transactions on Circuits and Systems – II Express Briefs 54 (4): 298-302. doi:10.1109/tcsii.2006.889713.
- ↑ Paynter, Henry (1992). An Epistemic Prehistory of Bond Graphs. pp. 10, 15 pages.
- ↑ Houpis, Constantine H.; Sheldon, Stuart N. (2013). «section 8.8». Linear Control System Analysis and Design with MATLAB®, Sixth Edition. Boca Raton, FL: CRC press. pp. 171-172. ISBN 9781466504264.
- ↑ For example: Baran, Thomas A.; Oppenhiem, Alan V. (2011), «INVERSION OF NONLINEAR AND TIME-VARYING SYSTEMS», 2011 Digital Signal Processing and Signal Processing Education Meeting (DSP/SPE), Digital Signal Processing Workshop and IEEE Signal Processing Education Workshop (DSP/SPE), IEEE, pp. 283-288, ISBN 978-1-61284-226-4, doi:10.1109/DSP-SPE.2011.5739226.
- ↑ a b Guilherme, J.; Horta, N. C.; Franca, J. E. (1999). SYMBOLIC SYNTHESIS OF NON-LINEAR DATA CONVERTERS. Archivado desde el original el 7 de noviembre de 2017. Consultado el 8 de marzo de 2019.
- ↑ BRZOZOWSKI, J.A.; McCLUSKEY, E. J. (1963). Signal Flow Graph Techniques for Sequential Circuit State Diagrams. IEEE. p. 97.
- ↑ Barry, J. R., Lee, E. A., & Messerschmitt, D. G. (2004). Digital communication (Third edición). New York: Springer. p. 86. ISBN 978-0-7923-7548-7.
- ↑ Happ, William W. (1964). «Application of flowgraph techniques to the solution of reliability problems». En Goldberg, M. F., ed. Physics of Failure in Electronics (AD434/329): 375-423. doi:10.1109/IRPS.1963.362257.
- ↑ Hall, John E. (23 de agosto de 2004). «The pioneering use of systems analysis to study cardiac output regulation». Am J Physiol Regul Integr Comp Physiol 287 (5): R1009-R1011. PMID 15475497. doi:10.1152/classicessays.00007.2004. Consultado el 20 de enero de 2015.
Otras lecturas[editar]
- Wai-Kai Chen (1976). Applied Graph Theory. North Holland Publishing Company. ISBN 978-0720423624. Wai-Kai Chen (1976). Applied Graph Theory. North Holland Publishing Company. ISBN 978-0720423624. Wai-Kai Chen (1976). Applied Graph Theory. North Holland Publishing Company. ISBN 978-0720423624. Wai-Kai Chen (1976). Applied Graph Theory. North Holland Publishing Company. ISBN 978-0720423624. Capítulo 3 para lo esencial, pero las aplicaciones están dispersas en todo el libro.
- Wai-Kai Chen (May 1964). «Some applications of linear graphs». Contract DA-28-043-AMC-00073 (E). Coordinated Science Laboratory, University of Illinois, Urbana.
- K. Thulasiraman; M. N. S. Swamy (1992). Graphs: Theory and Algorithms. 6.10-6.11 for the essential mathematical idea. ISBN 978-0-471-51356-8.
- Shu-Park Chan (2006). «Graph theory». En Richard C. Dorf, ed. Circuits, Signals, and Speech and Image Processing (3rd edición). CRC Press. § 3.6. ISBN 978-1-4200-0308-6. Shu-Park Chan (2006). «Graph theory». En Richard C. Dorf, ed. Circuits, Signals, and Speech and Image Processing (3rd edición). CRC Press. § 3.6. ISBN 978-1-4200-0308-6. Shu-Park Chan (2006). «Graph theory». En Richard C. Dorf, ed. Circuits, Signals, and Speech and Image Processing (3rd edición). CRC Press. § 3.6. ISBN 978-1-4200-0308-6. Shu-Park Chan (2006). «Graph theory». En Richard C. Dorf, ed. Circuits, Signals, and Speech and Image Processing (3rd edición). CRC Press. § 3.6. ISBN 978-1-4200-0308-6. Shu-Park Chan (2006). «Graph theory». En Richard C. Dorf, ed. Circuits, Signals, and Speech and Image Processing (3rd edición). CRC Press. § 3.6. ISBN 978-1-4200-0308-6. Shu-Park Chan (2006). «Graph theory». En Richard C. Dorf, ed. Circuits, Signals, and Speech and Image Processing (3rd edición). CRC Press. § 3.6. ISBN 978-1-4200-0308-6. Shu-Park Chan (2006). «Graph theory». En Richard C. Dorf, ed. Circuits, Signals, and Speech and Image Processing (3rd edición). CRC Press. § 3.6. ISBN 978-1-4200-0308-6. Compara los enfoques de los gráficos de Mason y Coates con el enfoque de k-tree de Maxwell.
- RF Hoskins (2014). «Flow-graph and signal flow-graph analysis of linear systems». En SR Deards, ed. Recent Developments in Network Theory: Proceedings of the Symposium Held at the College of Aeronautics, Cranfield, September 1961. Elsevier. ISBN 9781483223568. RF Hoskins (2014). «Flow-graph and signal flow-graph analysis of linear systems». En SR Deards, ed. Recent Developments in Network Theory: Proceedings of the Symposium Held at the College of Aeronautics, Cranfield, September 1961. Elsevier. ISBN 9781483223568. RF Hoskins (2014). «Flow-graph and signal flow-graph analysis of linear systems». En SR Deards, ed. Recent Developments in Network Theory: Proceedings of the Symposium Held at the College of Aeronautics, Cranfield, September 1961. Elsevier. ISBN 9781483223568. RF Hoskins (2014). «Flow-graph and signal flow-graph analysis of linear systems». En SR Deards, ed. Recent Developments in Network Theory: Proceedings of the Symposium Held at the College of Aeronautics, Cranfield, September 1961. Elsevier. ISBN 9781483223568. RF Hoskins (2014). «Flow-graph and signal flow-graph analysis of linear systems». En SR Deards, ed. Recent Developments in Network Theory: Proceedings of the Symposium Held at the College of Aeronautics, Cranfield, September 1961. Elsevier. ISBN 9781483223568. RF Hoskins (2014). «Flow-graph and signal flow-graph analysis of linear systems». En SR Deards, ed. Recent Developments in Network Theory: Proceedings of the Symposium Held at the College of Aeronautics, Cranfield, September 1961. Elsevier. ISBN 9781483223568. Una comparación de la utilidad del gráfico de flujo de Coates y el gráfico de flujo de Mason.