Pentágono

Para la sede del Departamento de Defensa de los Estados Unidos, véase El Pentágono

Un pentágono regular.

En geometría, se denomina pentágono (del griego πεντάγωνον, de πεντά, "cinco" y γωνον, "ángulos") a un polígono de cinco lados y cinco vértices.

Área de un pentágono

El área de un pentágono regular de lado a se puede obtener de la siguiente fórmula:

$A={\frac {5a^{2}}{4}}\cot {\frac {\pi }{5}}={\frac {a^{2}}{4}}{\sqrt {25+10{\sqrt {5}}}}\simeq 1.72048a^{2}$

De forma general si tenemos que el radio de la circunferencia circunscrita es r_u

$A={\frac {5}{8}}\cdot r_{u}^{2}\cdot {\sqrt {10+2{\sqrt {5}}}}$

o también:

$A={\frac {5}{2}}\cdot r_{u}^{2}\cdot \sin {72^{\circ }}$

Perímetro

Siempre que supongamos que el pentágono tiene lado a:

$a=2\cdot r_{u}\cdot \cos 54^{\circ }$

ó también:

$a=r_{u}\cdot {\sqrt {\frac {5-{\sqrt {5}}}{2}}}$

Para obtener el perímetro P de un pentágono regular, multiplíquese la longitud t de uno de sus lados por cinco (el número de lados n del polígono).

$P=n\cdot t=5\ t$

Fórmula para calcular los ángulos interiores

La suma de todos los ángulos interiores de un pentágono es 540°.

La fórmula general para calcular la suma de los ángulos interiores de cualquier polígono regular (en el caso del pentágono n = 5) es:

$\sum {\alpha =}(n-2)\cdot 180^{\circ }=3\cdot 180^{\circ }=540^{\circ }$

El ángulo comprendido entre dos lados de un pentágono regular se puede calcular mediante la siguiente fórmula (en el pentágono, n = 5):

$\alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {3}{5}}\cdot 180^{\circ }=108^{\circ }$

Trazado de un pentágono

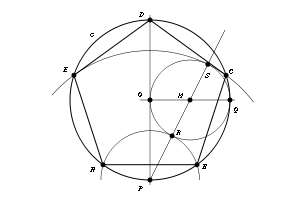
Podemos construir un pentágono, inscrito a una circunferencia c (véase la figura) de la siguiente manera:

Trazamos dos rectas perpendiculares por el centro O de la circunferencia (PD y OQ en la figura). Determinamos el punto medio M del segmento OQ y trazamos la recta PM. Con centro en M, trazamos la circunferencia de radio MO. Denotemos con R y S las intersecciones de esta circunferencia con la recta PM. Las circunferencias de centro en P y radios PR y PS determinan los vértices del pentágono regular.

• Uniendo los vértices del pentágono, se obtiene un pentagrama (estrella de 5 puntas) inscrito en él. En el centro, quedará otro pentágono regular, con lo que el proceso de inscribir pentagramas en los sucesivos pentágonos que se vayan generando, matemáticamente, no tiene fin.
• Al inscribir en un pentágono regular un pentagrama, se puede observar la razón áurea entre las longitudes de los segmentos resultantes.para sacar el area de un poligono se nesesita A=B X A

Propiedades geométricas del pentágono regular

Un pentágono regular es aquél que tiene todos sus lados y ángulos internos iguales. La suma de los ángulos internos de un pentágono regular vale (5-2)180° = 540° ó $3\pi$ radianes. Cada ángulo interno mide 108 grados ó $3\pi /5$ radianes. Así, por ejemplo (véase la figura), el ángulo BCD mide 108°.

Como los segmentos DE, EA, y AB son iguales, los arcos que ellos determinan en la circunferencia circunscrita son iguales. Esto implica que los tres ángulos DCE, ECA y ACB son iguales. Como la suma de ellos es 108°, cada uno de ellos mide 36°.

Cada ángulo externo del pentágono regular mide 72º ó $2\pi /5$ rad.

Relación con el número áureo

Veamos que la razón entre un segmento que una dos de sus vértices no consecutivos y uno de los lados del pentágono es la razón aúrea o número áureo, por ejemplo que

$CE=({\frac {1+{\sqrt {5}}}{2}})CD$

Por simetría, los segmentos CE y CA son iguales. Observamos que los triángulos ANF y CMF son semejantes. De la semejanza de sus lados tenemos que

${\frac {MC}{AN}}={\frac {FC}{AF}}$

Observemos que MC es la mitad de CE y que AN es la mitad de AB. Por otra parte, como el triángulo FCD es isósceles, tenemos que FC = CD. Así podemos escribir AF = AC - FC = CE - CD. Por tanto

${\frac {CE}{CD}}={\frac {CD}{CE-CD}}={\frac {1}{CE/CD-1}}$

Sustituyendo CE/CD por $\phi$ tenemos

$\phi ={\frac {1}{\phi -1}}\qquad \,(1)$

en otras palabras $\phi -1=1/\phi$. Esta ecuación describe la razón dorada. $\phi$ es el único número positivo que cuando le restamos la unidad, obtenemos su inverso.

De la discusión anterior se desprende: Si en un triángulo isósceles, el ángulo opuesto a la base vale 108°, la razón de la base del triángulo y uno de los otros lados es la razón dorada.

Algunas consideraciones sobre triángulos

Consideremos un pentágono (regular) y la circunferencia circunscrita a dicho pentágono. Tracemos la perpendicular por el centro de la circunferencia al lado DA del pentágono y sea M la intersección de esta perpendicular con la circunferencia El ángulo AOB mide 360°/5=72° y el ángulo AOM es su mitad, es decir 36°. El ángulo MOB, suma de estos dos vale 108° y como el triángulo AOB es isósceles tenemos que

1. La razón entre el segmento MB y el radio OM de la circunferencia es la razón dorada
2. $\angle BMO=(180^{\circ }-108^{\circ })/2=72^{\circ }/2=36^{\circ }$

Así, sea P la intersección de las rectas OA y MB. El triángulo PMO es isósceles, y la razón entre el radio OM y el segmento PM es la razón dorada. Finalmente, el triángulo OBP también es isósceles, con lo que PB = OB ( =OM). Tenemos

${\frac {PM}{OM}}={\frac {1}{\phi }}={\frac {MB-PB}{OM}}=\phi -1$

Lo anterior se puede interpretar como una demostración geométrica de la ecuacíon (1).

Algunas aplicaciones trigonométricas

$\sin {\frac {\pi }{10}}=\sin 18^{\circ }={\frac {{\sqrt {5}}-1}{4}}$

$\cos {\frac {\pi }{10}}=\cos 18^{\circ }={\frac {\sqrt {2(5+{\sqrt {5}})}}{4}}$

$\tan {\frac {\pi }{10}}=\tan 18^{\circ }={\frac {\sqrt {5(5-2{\sqrt {5}})}}{5}}$

$\cot {\frac {\pi }{10}}=\cot 18^{\circ }={\sqrt {5+2{\sqrt {5}}}}$

$\sin {\frac {\pi }{5}}=\sin 36^{\circ }={\frac {\sqrt {2(5-{\sqrt {5}})}}{4}}$

$\cos {\frac {\pi }{5}}=\cos 36^{\circ }={\frac {{\sqrt {5}}+1}{4}}$

$\tan {\frac {\pi }{5}}=\tan 36^{\circ }={\sqrt {5-2{\sqrt {5}}}}$

$\cot {\frac {\pi }{5}}=\cot 36^{\circ }={\frac {\sqrt {5(5+2{\sqrt {5}})}}{5}}$

Véase también

• Anexo:Ecuaciones de figuras geométricas
• Triángulo
• Cuadrado
• Hexágono
• Heptágono
• Octógono
• Eneágono
• Decágono

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre pentágonos.
• Wikcionario tiene definiciones y otra información sobre pentágono.
• Una posibilidad de poder ver pentágonos exactos mediante SVG se puede encontrar en Wikimedia Commons