Logaritmo

Representación gráfica de logaritmos en varias bases:
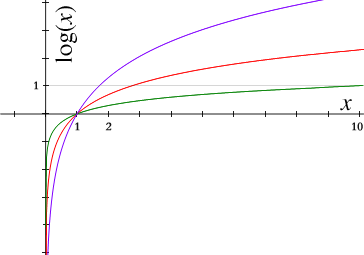
el rojo representa el logaritmo en base e,
el verde corresponde a la base 10,
y el púrpura al de la base 1,7.

En matemática, el logaritmo es una función matemática inversa de la función exponencial.

El logaritmo (con base b) de un número x es el exponente n al que hay que elevar la base dada b, para que nos de dicho número x.

$\log _{b}x=n\Leftrightarrow \ x=b^{n}$

La base b tiene que ser positiva y distinta de 1 $(b>0,b\neq 1)$.

Introducción

Dado un número real (argumento x), la función logaritmo le asigna el exponente n (o potencia) a la que un número fijo (base b) se ha de elevar para obtener dicho argumento. Es la función inversa de la exponencial x = bⁿ. Esta función se escribe como: n = log_b x, lo que permite obtener n. Así, en la expresión 10² = 100, el logaritmo de 100 en base 10 es 2, y se escribe como log₁₀ 100 = 2.

Por ejemplo: $3^{4}=81\longmapsto \log _{3}81=4\,\!$

Se denomina logaritmo neperiano o logaritmo natural (ln) al logaritmo en base e de un número o resutado dado por el exponente.

Historia

El método de cálculo mediante logaritmos fue propuesto por primera vez, públicamente, por John Napier (latinizado Neperus) en 1614, en su libro titulado Mirifici Logarithmorum Canonis Descriptio. Joost Bürgi, un matemático y relojero suizo al servicio del duque de Hesse-Kassel, concibió por vez primera los logaritmos, sin embargo, publicó su descubrimiento cuatro años después que Napier. La inicial resistencia a la utilización de logaritmos fue cambiada por Kepler, por el entusiasta apoyo de su publicación y la impecable y clara explicación de cómo funcionaban.

Este método contribuyó al avance de la ciencia, y especialmente de la astronomía, facilitando la resolución de cálculos muy complejos. Los logaritmos fueron utilizados habitualmente en geodesia, navegación y otras ramas de la matemática aplicada, antes de la llegada de las calculadoras y computadoras. Además de la utilidad en el cálculo, los logaritmos también ocuparon un importante lugar en las matemáticas más avanzadas; el logaritmo natural presenta una solución para el problema de la cuadratura de un sector hiperbólico ideado por Gregoire de Saint-Vincent en 1647.

Napier no usó una base tal como ahora se entiende pero, sus logaritmos, como factor de escala, funcionaban de manera eficaz con base 1/e. Para los propósitos de interpolación y facilidad de cálculo, eran útiles para hallar la relación r en una serie geométrica tendente a 1. Napier escogió r = 1 - 10⁻⁷ = 0,999999 (Bürgi eligió r = 1 + 10⁻⁴ = 1,0001). Los logaritmos originales de Napier no tenían log 1 = 0, sino log 10⁷ = 0. Así, si N es un número y L es el logaritmo, Napier calcula: N = 10⁷(1 − 10⁻⁷)^L. Donde (1 − 10⁻⁷)¹⁰⁷ es aproximadamente 1/e, haciendo L/10⁷ equivalente a log_1/e N/10⁷.

La definición moderna y su explicación aparece en 1866, en un diccionario de Ciencia, Literatura, y Arte: Comprende las definiciones y derivaciones de la Ciencia en términos de uso general, junto con la Historia y descripción de los principios científicos de casi todos los sectores del conocimiento humano.

Etimología

Inicialmente, Napier llama "números artificiales" a los logaritmos y "números naturales" a los antilogaritmos. Más tarde, Napier usa la palabra logaritmo en el sentido de un número que indica una proporción: λόγος (logos) el sentido de proporción, y ἀριθμός (arithmos) significado número, y se define, literalmente, como un número que indica una relación o proporción. Se refiere a la proposición que fue hecha por Napier en su "teorema fundamental", que establece que la diferencia de dos logaritmos determina la relación de los números a los cuales corresponden, de manera que una serie aritmética de logaritmos corresponde a una serie geométrica de números. El término antilogaritmo fue introducido a finales de siglo XVII y, aunque nunca se utilizó ampliamente en matemáticas, perduró en muchas tablas, hasta que cayó en desuso.

Definición analítica

En la imagen se puede ver la representación gráfica del logaritmo neperiano, como también la representación de las rectas tangentes a la función en x = e (T_e) y en x = 1 (T₁).

Podemos introducir la función logarítmica como una función analítica que es de hecho la función primitiva de otra función analítica bien conocida. Para definir de esa manera el logaritmo empezamos con algunas observaciones:

1. La derivada de la función $f(x)=x^{n}\,\!$ es $f^{\prime }(x)=nx^{n-1}\,\!$. Al dividir ambos lados de la expresión entre "n" y observar el resultado, se puede afirmar que una primitiva de $x^{m}\,\!$ es ${x^{m+1}}/{m+1}\,$ (con $m=n-1\,$).
2. Este cálculo obviamente no es válido cuando $m=-1$, porque no se puede dividir por cero. Por lo tanto, la función inversa $1/x\,$ es la única función "potencia" que no tiene una primitiva "potencia".
3. Sin embargo, la función $1/x\,$ es continua sobre el rango $(0,+\infty )$ lo que implica que tiene forzosamente una primitiva en este intervalo, y también sobre $(-\infty ,0)$.

A la función analítica cuya existencia se deduce de las observaciones anteriores la llamaremos función logaritmo, y la definiremos convencionalmente como:

$[\ln(x)]^{\prime }={\frac {1}{x}},\qquad \ln(1)=0$

Propiedades

• La función $\ln(x)\,$ definida anteriormente es estrictamente creciente pues su derivada es estrictamente positiva
• Tiene límites infinitos en $0^{+}\,$ y en $+\infty$.
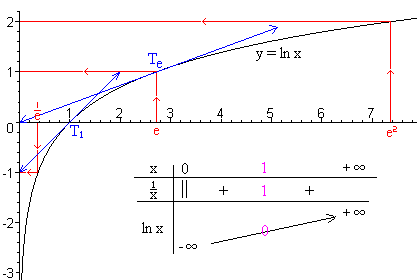
• La tangente T_e que pasa por el punto de abscisa e de la curva, pasa también por el origen.
• La tangente T₁ que pasa por el punto de abscisa 1 de la curva, tiene como ecuación: $y=x-1$.
• La derivada de segundo orden es $\ln ^{\prime \prime }(x)={-1}/{x^{2}}\,$, siempre negativa., por lo tanto la función es cóncava, hacia abajo, como la forma que tiene la letra "n", es decir que todas las tangentes pasan por encima de la curva. Es lo que se constata con T₁ y T_e.

Uso de logaritmos

La función $log_{b}(x)=a$ está definida donde quiera que x es un número real positivo y b es un número real positivo diferente a 1. Véase identidades logarítmicas para diversas reglas relacionadas a las funciones logarítmicas. También es posible definir logaritmos para argumentos complejos.

Para enteros b y x, el número $log_{b}(x)$ es irracional (no puede representarse como el cociente de dos enteros) si b o x tiene un factor primo que el otro no tiene.

Logaritmo natural

En análisis matemático se llama logaritmo natural o logaritmo neperiano a la primitiva de la función:
$f(x)={\frac {1}{x}}\,\!$ que toma el valor 1 cuando la variable x es igual a 1, es decir:

$\ln(x)=\int _{1}^{x}{\frac {dt}{t}}$ para x > 0.

También se llama así al logaritmo obtenido tomando como base el valor del número trascendental "e" (aproximadamente igual a 2,718.281.828...).

La función logaritmo natural es la inversa de la función exponencial: $f(x)=e^{x}\;$.

Números reales

El logaritmo natural de un número real positivo está bien definido y es un número real. Sin embargo, generalizar el logaritmo natural a números reales negativos sólo puede hacerse introduciendo números complejos.

Sin embargo, al igual que sucede el logaritmo de números complejos la elección de logaritmo de un número negativo no es única, aunque la elección hecha es la más frecuentemente usada para extender el logaritmo a números reales negativos.

Números complejos

El logaritmo natural de un número complejo z es otro número complejo b = ln(z) que sea solución de la ecuación:

(*)$z=e^{b}\;$

Sin embargo trabajando con números complejos aparece una dificultad que no aparecía con los números reales positivos, y es que la ecuación anterior no tiene solución única. De hecho, tiene un número infinito de soluciones, aunque todas ellas son fáciles de encontrar. Dado un número complejo z escrito en forma polar una solución posible de la ecuación (*) es b₀:

$b_{0}=\ln \rho +i\theta \qquad {\mbox{con}}\ z=\rho e^{i\theta }$

Puede comprobarse que esta no es la única solución, sino que para cualquier valor $k\in \mathbb {Z}$ resulta que el número complejo b_k, definido a continuación, también es solución:

$b_{k}=\ln \rho +i\theta +2\pi ki\qquad \Rightarrow e^{b_{k}}=\rho e^{i\theta }\cdot e^{2\pi ki}=z$

De hecho cada valor particular de k define una superficie de Riemann.

Matrices

Una matriz B es logaritmo de una matriz dada A si la exponenciación de B es A:

$e^{B}=A.\,$

A diferencia de la exponenciación de matrices, el logaritmo de una matriz real puede no estar definido siempre.

En el caso de una matriz diagonalizable es necesario que logaritmo esté definido para todos y cada uno de los autovalores o valores propios de la matriz. En ese caso el logaritmo de la matriz está definido y es una matriz real. Para una matriz real, tal que el logaritmo no está definido sobre el espectro o conjunto de autovalores entonces al igual que sucedía con los números reales negativos y los complejos aun así es posible definir una matriz logaritmo aunque esta no está definida unívocamente.

En el caso de una matriz no diagonalizable, este proceso es más complicado, ya que requiere encontrar la forma canónica de Jordan de la matriz.

Identidades logarítmicas

Los logaritmos mantienen ciertas identidades aritméticas muy útiles a la hora de realizar cálculos:

• El logaritmo de un producto es igual a la suma de los logaritmos de los factores.

$\!\,\log(ab)=\log(a)+\log(b)$

• El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.

$\!\,\log(a/b)=\log(a)-\log(b)$

• El logaritmo de una potencia es igual al producto entre el exponente y el logaritmo de la base de la potencia.

$\!\,\log(a^{x})=x\log(a)$

• El logaritmo de una raíz es igual al producto entre la inversa del índice y el logaritmo del radicando.

$\!\,\log({\sqrt[{x}]{y}})={\frac {\log(y)}{x}}$

Logaritmo en base b (cambio de base)

Son comunes los logaritmos en base e (logaritmo neperiano), base 10 (logaritmo común), base 2 (logaritmo binario), o en base indefinida (logaritmo indefinido). La elección de un determinado número como base de los logaritmos no es crucial, debido a que se pueden hacer conversiones de una base a otra de forma sencilla. Para ello, es útil la siguiente fórmula que define al logaritmo de x en base b (suponiendo que b, x, y k son números reales positivos y que tanto "b" como "k" son diferentes de 1):

$\log _{b}(x)={\frac {\log _{k}(x)}{\log _{k}(b)}}\,\!$

en la que "k" es cualquier base válida. Si hacemos k=x, obtendremos:

$\log _{b}(x)={\frac {1}{\log _{x}(b)}}\,\!$

En la práctica, se emplea el logaritmo decimal, que se indica como $\log(x)\,\!$, en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada pH) y en física en magnitudes como la medida de la luminosidad (candela), del sonido(dB), de la energía de un terremoto (escala de Richter), etc. En informática se usa el logaritmo en base 2 la mayoría de veces. Las propiedades de los logaritmos son una base que facilita aún más su resolución.

Logaritmo en base imaginaria

Un logaritmo en base imaginaria es un logaritmo que tiene como base i (la unidad imaginaria). Este tipo de logaritmos se puede resolver fácilmente con la fórmula:

$\log _{i}(z)={{2\ln(z)} \over i\pi }.\,$

Dónde z es cualquier número complejo excepto 0.

Véase también

• Neper
• Número e
• Logaritmo en base imaginaria
• Logaritmo binario
• Logaritmo de una matriz
• Exponenciación
• pH
• Decibelio (dB) unidad logarítmica para expresar la relación entre dos magnitudes, acústicas o eléctricas.
• Los logaritmos son utilizados en la escala sismológica de Richter.

Enlaces externos

• Logaritmación en Enciclopedia libre universal en español
• Wikimedia Commons alberga una galería multimedia sobre Logaritmo.
• Completísimo documento en español sobre logaritmo (formato PDF, 58 páginas).
• Enciclopedia de Logaritmos
• Videos de Logaritmos