Función (matemática)

Función de X en Y: la condición de existencia asegura que de cada elemento sale alguna flecha y la de unicidad que sólo sale una.

En Matemáticas, dados dos conjuntos X e Y, una función o aplicación de X en Y es una correspondencia matemática denotada

$f\colon X\to Y\,$

que cumple con las siguientes dos condiciones:

Condición de existencia: Todos los elementos de X están relacionados con elementos de Y, es decir, $\forall x\in X,\ \exists y\in Y\ \backslash \ (x,y)\in f.$ Condición de unicidad: Cada elemento de X esta relacionado con un único elemento de Y, es decir, si $(x,y_{1})\in f\land (x,y_{2})\in f\Rightarrow y_{1}=y_{2}.$

Una función es un caso particular de relación y de correspondencia matemática. Cada relación o correspondencia de un elemento $x\in X$ con un (y sólo un) $y\in Y$ se denota $f(x)=y\,$, en lugar de $(x,y)\in f.$

Propiedades

Dominio

El dominio de $f\,$ es el conjunto de existencia de la misma, es decir, los elementos para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota ${\rm {Dom}}_{f}\,$ o bien ${\rm {D}}_{f}\,$ y está definido por:

$D_{f}=\;\left\{x\in X\;:\;\exists y\in Y,\;f(x)=y\right\}$

Recorrido o codominio

El recorrido o conjunto de llegada de $f\,$ es el conjunto $Y,\,$ y se denota ${\rm {Rec}}_{f}\,$ o bien ${\rm {C}}_{f}.\,$

Rango

El rango de $f\,$ está formada por los valores que alcanza la misma. Es el conjunto de todos los objetos transformados, se denota ${\rm {Ran}}_{f}\,$ o bien ${\rm {R}}_{f}\,$ y está definida por:

${\rm {R}}_{f}=\left\{y\in Y\;\backslash \;\exists x\in X,\;f(x)=y\right\}$

Preimagen

Una preimagen de un $y\in Y$ es algún $x\in X$ tal que $f(x)=y\,.$

Note que ${\rm {D}}_{f}=X\,$, y que algunos elementos del recorrido pueden no ser imagen de ningún elemento del dominio. En efecto, puede darse que $\exists y\in Y$ tal que $\forall x\in X,\;f(x)\neq y.$

Ejemplos

• La función definida por $f(x)=x+1\,$, tiene como dominio e imagen todos los números reales $(\mathbb {R} ).$

Función con Dominio X y Codominio Y

• Para la función $g(x)=x^{2}\,$, en cambio, si bien su dominio es $\mathbb {R}$, sólo tendrá como imagen los valores comprendidos entre 0 y +∞ que sean el cuadrado de un número real.

• En la figura se puede apreciar una función $f\colon X\to Y\,$, con

${\rm {Dom}}_{f}=X=\{1,2,3,4\}\,$

${\rm {Rec}}_{f}\ =\;Y=\{a,b,c,d\}\,$

Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el $1$ y el $4$). Finalmente,

${\rm {Im}}_{f}=\{b,c,d\}\subseteq Y.$

Esta función representada como relación, queda: $X\times Y=\{(1,b),(2,c),(3,d),(4,b)\}$

Representación de funciones

Las funciones se pueden representar de distintas maneras:

• Como expresión matemática: ecuaciones de la forma $y=f(x)$, que permiten representar el comportamiento de la función a lo largo de todo su dominio.

Ejemplo: y=x+2.

• Como tabulación: tabla que permite representar algunos valores discretos de la función.

Ejemplo:

   X| -2 -1  0  1  2  3
   Y|  0  1  2  3  4  5

• Como pares ordenados: pares ordenados, muy usados en teoría de grafos.

Ejemplo: A={(-2, 0),(-1, 1),(0, 2),(1, 3), ... (x, x+2)}

• Como proposición: una descripción por comprensión de lo que hace la función.

Ejemplo: "Para todo x, número entero, y vale x más dos unidades".

• Como gráfica: gráfica que permite visualizar tendencias en la función. Muy utilizada para las funciones continuas típicas del cálculo, aunque también las hay para funciones discretas.

Ejemplo:

5						X
4					X
3				X
2			X
1		X
0	X
y / x	-2	-1	0	1	2	3

Funciones según el tipo de aplicación

Dados dos conjuntos X, Y, y todas las posibles aplicaciones que pueden formarse entre estos dos conjuntos, se pueden diferenciar los siguientes casos:

• Si a cada imagen le corresponde un único origen, inyectiva.
• Si la aplicación es sobre todo el conjunto final, sobreyectiva.

Además de estos dos casos característicos, una aplicación puede ser inyectiva y sobreyectiva simultáneamente, que se denominan biyectiva, o ninguna de ellas en cuyo caso no tiene un nombre especifico.

Vamos a representar los tipos de aplicaciones en un Diagrama de Venn, el conjunto universal U, representado por un rectángulo, es el de todas las posibles aplicaciones, el conjunto A es el de las aplicaciones inyectivas, y el conjunto B el de las sobreyectivas, esto nos permite ver los distintos tipos de aplicaciones de un modo gráfico.

Aplicación inyectiva y no sobreyectiva

Aplicación inyectiva y no sobreyectiva

Una aplicación inyectiva cada elemento imagen tendrá un único origen y una no sobreyectiva tendrá al menos un elemento del conjunto final que no tenga elemento origen.

En el diagrama de Venn corresponden a las aplicaciones que pertenecen a A y no pertenecen a B, esto es las que pertenecen a la diferencia de A y B: A-B.

En estas aplicaciones la cardinalidad de X es siempre menor que la de Y, esto es el conjunto Y tendrá mayor número de elementos que X cuando tratamos de compararlos.

Ejemplo

en el diagrama de la figura:

todos los elementos de Y, que tienen origen, tienen un único origen, esto hace que la aplicación sea inyectiva

el elemento d de Y, no tiene ningún origen por lo que esta aplicación no es sobreyectiva.

Segundo ejemplo

Partiendo del conjunto de pinceles con pintura de colores:

$P=\{\,$

,

,

$\}\,$

Sobre el conjunto de caras pintadas:

$C=\{\,$

,

,

,

$\}\,$

Asociando cada pincel con la cara correspondiente:

Dado que cada pincel tiene una cara y solo una cara de su color esta correspondencia es una aplicación, como las caras que tiene pincel de su color, tienen un solo pincel de su color, la aplicación es inyectiva, y como la cara pintada de amarillo, no tiene ningún pincel de este color, la aplicación no es sobreyectiva.

Aplicación no inyectiva y sobreyectiva

Aplicación no inyectiva y sobreyectiva

Una aplicación no inyectiva tiene al menos un elemento imagen que tiene dos o más orígenes y una sobreyectiva todos los elementos del conjunto final tienen al menos un elemento origen.

En el diagrama de Venn corresponden a las aplicaciones que no pertenecen a A y si pertenecen a B, esto es las que pertenecen a la diferencia de B y A: B-A.

Para esta aplicación el conjunto X ha de tener mayor número de elementos que Y, la cardinalidad de X ha de ser mayor que la de Y.

Ejemplo

en el diagrama de la figura:

el elemento c de Y, tiene dos orígenes: el 3 y el 4, por lo que esta aplicación no es inyectiva.

todos los elementos de Y, tienen origen, esto hace que la aplicación sea sobreyectiva.

Segundo ejemplo

Igual que en el ejemplo anterior partiremos del conjunto de pinceles con pintura de colores:

$P=\{\,$

,

,

,

$\}\,$

En este caso hay dos pinceles con pintura azul, pero a pasar de tener el mismo color de pintura son dos pinceles distintos.

Como conjunto final tenemos el conjunto de caras pintadas:

$C=\{\,$

,

,

$\}\,$

Asociando cada pincel con la cara del mismo color, vemos que cada pincel tiene una cara pintada de su color y solo una, esto hace que la correspondencia sea una aplicación, la cara azul tiene dos pinceles de su mismo color, por lo que no es inyectiva, todas las caras tiene un pincel con su color, luego la aplicación es sobreyectiva.

Aplicación inyectiva y sobreyectiva (biyectiva)

Aplicación biyectiva

Si una aplicación es inyectiva y sobreyectiva simultáneamente, se denomina biyectiva. Por ser inyectiva los elementos que tienen origen tienen un único origen y por ser sobreyectiva todos los elementos del conjunto final tienen origen.

En el diagrama de Venn el conjunto A es el de las aplicaciones inyectiva y el conjunto B el de las aplicaciones sobreyectiva, las aplicaciones biyectiva, que son inyectiva y sobreyectiva, será la intersección de A y B.

Estas dos circunstancias dan lugar a que el conjunto X e Y tengan el mismo número de elementos, la cardinalidad de X es la misma que la de Y, esto tiene una gran importancia cuando se pretende comparar dos conjuntos:

• Si dados dos conjuntos podemos encontrar una aplicación biyectiva entre ellos, podemos afirmar, que los dos conjuntos tienen el mismo número de elementos. La cardinalidad de X es igual a la de Y.

Ejemplo

f(x)= 2x

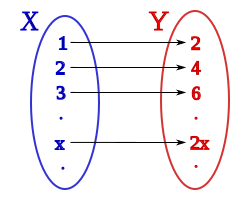
en el diagrama de la figura:

todos los elementos de Y, que tienen origen, tienen un único origen, esto hace que la aplicación sea inyectiva

todos los elementos de Y, tienen origen, esto hace que la aplicación sea sobreyectiva.

Si tomaremos por conjunto inicial el conjunto de los números naturales:

$X=\{1,2,3,...\}\,$

y por conjunto final el de los números naturales pares:

$Y=\{2,4,6,...\}\,$

Podemos ver que la relación

$f:X\rightarrow Y$

$f:x\mapsto 2x$

Por el que a cada número natural x de X, le asociamos un número par 2x de Y, se cumple:

1. f: es una aplicación, dado que a cada uno de los valores x de X le corresponde un único valor 2x de Y.
2. esta aplicación es inyectiva dado que a cada número par 2x de Y le corresponde un único valor x de X.
3. y es sobreyectiva porque todos los números pares tienen un origen

Esto nos permite afirmar que hay el mismo número de números naturales que de números naturales pares, se da la paradoja de que los números naturales pares en un subconjunto propio de los números naturales, esta circunstancia solo se da con los conjuntos infinitos.

Segundo ejemplo

Tomando el conjunto de pinceles como conjunto inicial:

$P=\{\,$

,

,

,

$\}\,$

y el de caras como conjunto final:

$C=\{\,$

,

,

,

$\}\,$

La correspondencia que asocia cada pincel con la cara de su mismo color es una aplicación porque todos los pinceles tienen una cara con su color y solo una cara de ese color, la aplicación es inyectiva porque un pincel corresponde con una sola cara, y es sobreyectiva porque todas las caras tiene un pincel de su color, al ser inyectiva y sobreyectiva simultáneamente esta aplicación es biyectiva.

Una aplicación biyectiva hace corresponder los elementos del conjunto inicial con los del conjunto final uno a uno, pudiéndose decir que hay el mismo número de elementos en el conjunto inicial que en el final.

Aplicación no inyectiva y no sobreyectiva

Aplicación no inyectiva y no sobreyectiva

Una aplicación no inyectiva tendrá al menos un elemento imagen que tenga dos o más orígenes y una no sobreyectiva tendrá al menos un elemento del conjunto final que no tenga elemento origen. Este tipo de aplicaciones no tiene un nombre especifico y quizá sean las que presenten, desde el punto de vista matemático, un menor interés.

Para esta aplicación los conjuntos X e Y no son comparables, y no podemos plantear ningún supuesto sobre su cardinalidad, partiendo de su comparación, ni sobre su número de elementos.

En el diagrama de Venn corresponden a las aplicaciones que no pertenecen a A y no pertenecen a B, esto es las que no pertenecen a la unión de A y B.

Ejemplo

en el diagrama de la figura:

el elemento b de Y, tiene dos orígenes: 1 y 2, esto hace que esta aplicación no sea inyectiva

el elemento a de Y, no tiene ningún origen por lo que esta aplicación no es sobreyectiva

Segundo ejemplo

Si tomamos como conjunto inicial el de pinceles de colores:

$P=\{\,$

,

,

,

$\}\,$

y como conjunto final el de caras coloreadas:

$C=\{\,$

,

,

,

$\}\,$

Vemos que todos los pinceles tiene una cara y solo una cara de su mismo color, luego esta correspondencia es una aplicación matemática.

Como la cara azul tiene dos pinceles de su color la aplicación no es inyectiva, y como la cara amarilla no tiene ningún pincel de ese color no es sobreyectiva, luego esta aplicación es no inyectiva y no sobreyectiva.

Resumen

Sobreyectiva, no inyectiva

Inyectiva, no sobreyectiva

Biyectiva

No sobreyectiva, no inyectiva

Álgebra de las funciones

Composición de funciones

Dadas dos funciones f: A → B y g: B → C, donde la imagen de f está contenida en el dominio de g, se define la función composición (g ο f ): A → C como (g ο f)(x) = g (f(x)), para todos los elementos x de A.

$A\to \,\,B\;\;\to \;\;\,C$

$x\mapsto f(x)\mapsto g(f(x))$

Función identidad

Dado un conjunto $\,A\,$, la función $\;e_{A}\colon A\to A\,$ que asigna a cada $x\,$ de $A\,$ el mismo $x\,$ de $A\,$ se denomina función identidad o función unitaria.

$e_{A}=\left\{(x,x)\mid x\in A\right\}$

Dada cualquier función $g\colon A\to B\,$, es claro que $e_{B}\circ f\colon A\to B\,$ es igual a $f\,$ y que $f\circ e_{A}\colon A\to B\,$ es también igual a $f\,$, puesto que para todo $x\;\;f(e_{A}(x))=f(x)$ y también $\;\;e_{B}(f(x))=f(x)$

$\;e_{B}\circ f=f\circ e_{A}=f\;$

Función inversa

Dada una función $f\colon A\to B\,\;$, se denomina función inversa de $f\;$, $f^{-1}\colon B\to A\,$ a la función que cumple la siguiente condición:

$\;f^{-1}\circ f=e_{A}\;$

$\;f\circ f^{-1}=e_{B}\;$

Si existe una función que cumpla esas dos condiciones, ser inversa por la izquierda y ser inversa por la derecha, se demuestra que esa función es única. Eso justifica la notación $f^{-1}\;$, que sería ambigua si pudiera haber dos inversas de la misma función.

Sólo algunas funciones tienen inversa. De hecho, la condición necesaria y suficiente para la existencia de $f^{-1}\;$ es que $f\;$ sea biyectiva. Por tanto, las afirmaciones

• Existe función inversa de $f\;$ y
• $f\;$ es biyectiva

son lógicamente equivalentes.

El grupo de las funciones biyectivas

Considerando todas las funciones biyectivas $f\colon \,A\to A$, las conclusiones del apartado anterior pueden resumirse en:

1. Dadas tres funciones la operación de composición es asociativa: $(f_{i}\circ f_{j})\circ f_{k}=f_{i}\circ (f_{j}\circ f_{k})\,$
2. $\exists e_{A}\colon \,A\to A\,$ tal que $\forall f\colon A\to A$ tenemos $f\circ e_{A}=e_{A}\circ f=f$
3. $\forall f\colon \,A\to A\,\exists f^{-1}\colon \,A\to A\mid f^{-1}\circ f=f\circ f^{-1}=e_{A}$

Estas tres condiciones determinan un grupo. El conjunto de las funciones biyectivas $A\to A$ es un grupo con respecto a la operación de composición de funciones y recibe el nombre de grupo simétrico de $A\,$.

Funciones en Rⁿ según su número de variables

Siempre es posible restringir tanto el dominio como la imagen de una función con un propósito determinado. Por ejemplo, es completamente válido restringir $g(x)=x^{2}\,$ al dominio de los números naturales, para que el conjunto imagen tome así los valores comprendidos en el intervalo [0,+∞[.

Además, el dominio y la imagen pueden tener cualquier número de variables. Dicho número permite clasificar a las funciones como sigue:

• Función escalar: Función del tipo $\mathbb {R} \ \rightarrow \mathbb {R} .$
• Campo escalar: Función del tipo $\mathbb {R} ^{n}\rightarrow \mathbb {R} .$
• Función vectorial: Función del tipo $\mathbb {R} \ \rightarrow \mathbb {R} ^{n}.$
• Campo vectorial: Función del tipo $\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{m}.$

Funciones reales de variable real

Los anteriores apartados se han referido a funciones entre conjuntos cualesquiera. Las funciones entre conjuntos de números, y particularmente las funciones $\mathbb {R} \to \mathbb {R}$, o funciones reales de variable real son particularmente relevantes por la diversidad de sus aplicaciones prácticas y por sus particulares propiedades matemáticas. En algunos textos se reserva para las funciones entre conjuntos de números el término función mientras que a las funciones entre conjuntos cualesquiera se las denomina aplicaciones. A continuación se detallan algunas propiedades y definiciones de interés referidas a las funciones definidas $\mathbb {R} \to \mathbb {R}$ o entre conjuntos de números ($\mathbb {N,Z,Q,R,C}$).

Funciones reales y funciones discretas

• Si el dominio de una función es un intervalo de la recta real la función se denominará real. En cambio, si la función está definida para los números enteros se denominará función discreta. Un ejemplo de una función discreta son las sucesiones.

Funciones acotadas

• Una función se denomina acotada si su conjunto imagen está acotado, por ejemplo: f(x) = sen(x) y g(x) = cos(x) tienen por conjunto imagen el intervalo [-1,1]. Si su conjunto imagen está acotado sólo superior o inferiormente, se dice que la función está acotada superior o inferiormente, respectivamente. Por ejemplo, f("x")=|x| tiene por conjunto imagen $[0,+\infty [\;\!$, por lo que está acotada inferiormente.

Funciones pares e impares

Se dice que una función es par cuando presenta simetría sobre el eje de ordenadas, esto es, si

$x>\forall x(x\in A\land -x\in A\rightarrow f(x)=f(-x))$

Una función es impar si presenta simetría con respecto al origen de coordenadas, esto es si

$\forall x(x\in A\land -x\in A\rightarrow f(-x)=-f(x))$

Una función que no presenta simetría par no tiene necesariamente simetría impar. Algunas funciones no presentan ninguno de los dos tipos de simetría o bien la presentan frente a focos o ejes distintos del origen de coordenadas o el eje de ordenadas (o eje Y). Dichas funciones se dice que no poseen paridad.

Funciones monótonas

1. La función f es estrictamente creciente en $[a,b]\leftrightarrow \forall x_{1},x_{2}\in [a,b]:x_{1}<x_{2}\leftrightarrow f(x_{1})<f(x_{2})$
2. f es estrictamente decreciente en $[a,b]\leftrightarrow \forall x_{1},x_{2}\in [a,b]:x_{1}<x_{2}\leftrightarrow f(x_{1})>f(x_{2})$

Si una función es estrictamente creciente o decreciente entonces es inyectiva.

1. f es creciente en $[a,b]\leftrightarrow \forall x_{1},x_{2}\in [a,b]:x_{1}<x_{2}\leftrightarrow f(x_{1})\leq f(x_{2})$
2. f es decreciente en $[a,b]\leftrightarrow \forall x_{1},x_{2}\in [a,b]:x_{1}<x_{2}\leftrightarrow f(x_{1})\geq f(x_{2})$

Si una función verifica cualquiera de las cuatro propiedades anteriores se dice que es monotona.

Funciones periódicas

Una función es periódica si se cumple: $f(x)=f(x+T);T\neq 0\,$ donde $T\,$ es el período.

En particular, una función es periódica alternada cuando se cumple: $f(x)=-f\left(x+{\frac {T}{2}}\right)\,$. Estas últimas también son conocidas como funciones simétricas de media onda y constan de dos semiondas iguales de sentidos opuestos.

Funciones cóncavas y convexas

Función convexa.

Una función es convexa en un intervalo si la rectas tangentes a la función en ese intervalo están por debajo de la función. Una función es cóncava en un intervalo si la rectas tangentes a la función de ese intervalo están por encima.

La denominación de convexidad y concavidad depende del punto de vista que se adopte para considerar que es una concavidad, esto es si se mira a la función "desde arriba" o "desde abajo". Por ello, algunos textos denominan convexas a las funciones que se curvan "hacia abajo", al contrario de la definición que se acaba de dar en los anteriores párrafos. Por ello, es frecuente que en ocasiones se adopten las denominaciones concava hacia arriba y concava hacia abajo para evitar las ambigüedades.

Las técnicas del análisis diferencial permiten determinar si una función es creciente, decreciente, concava o convexa a través del estudio de las derivadas sucesivas de la función.

Véase también

• Funciones matemáticas
• Continuidad (matemática)
• Asíntotas de una función
• Función lineal
• Sucesión matemática

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre funciones.
• FooPlot - Graficador de funciones matemáticas
• En la Enciclopedia en-línea de la Springer-Verlag: [1]
• The function concept - Sobre la historia del concepto de función