Equilibrio vapor-líquido
En termodinámica e ingeniería química, el equilibrio vapor-líquido (VLE) describe la distribución de una especie química entre la fase de vapor y una fase líquida.
La concentración de un vapor en contacto con su líquido, especialmente en equilibrio, se expresa a menudo en términos de presión de vapor, que será una presión parcial (una parte de la presión total del gas) si hay otros gases presentes con el vapor. La presión de vapor de equilibrio de un líquido depende en general en gran medida de la temperatura. En el equilibrio vapor-líquido, un líquido con componentes individuales en ciertas concentraciones tendrá un equilibrio de vapor en el cual las concentraciones o presiones parciales de los componentes de vapor tienen ciertos valores dependiendo de todas las concentraciones del componente líquido y de la temperatura. Lo contrario también es cierto: si un vapor con componentes a ciertas concentraciones o presiones parciales se encuentra en equilibrio vapor-líquido con su líquido, entonces las concentraciones de componentes en el líquido se determinarán dependiendo de las concentraciones de vapor y de la temperatura. La concentración de equilibrio de cada componente en la fase líquida es a menudo diferente de su concentración (o presión de vapor) en la fase de vapor, pero existe una relación. Los datos de concentración de VLE pueden ser determinados experimentalmente, o computados o aproximados con la ayuda de teorías tales como ley de Raoult, ley de Dalton, y ley de Henry.
Tal información de equilibrio vapor-líquido es útil en el diseño de columnas para destilación, especialmente destilación fraccionada, que es una especialidad particular del ingeniero químico.[1][2][3] La destilación es un proceso utilizado para separar total o parcialmente los componentes de una mezcla por ebullición (vaporización) seguida de condensación. La destilación aprovecha las diferencias de concentración de los componentes en las fases líquida y vapor.
En las mezclas que contienen dos o más componentes, las concentraciones de cada uno se expresan a menudo como fracciones molares. La fracción molar de un componente dado de una mezcla en una fase particular (ya sea la fase de vapor o la fase líquida) es el número de moles de ese componente en esa fase dividido por el número total de molares de todos los componentes en esa fase.
Las mezclas binarias son las que tienen dos componentes mientras que las mezclas de tres componentes se denominan mezclas ternarias. Puede haber datos VLE para mezclas con aún más componentes, pero tales datos son a menudo difíciles de mostrar gráficamente, a este tipo de mezclas se les conoce como multicomponente. Los datos VLE son una función de la presión total, como 1 atm o cualquier presión a la que se lleve a cabo el proceso.
Cuando se alcanza una temperatura tal que la suma de las presiones de vapor de equilibrio de los componentes líquidos se vuelve igual a la presión total del sistema (de lo contrario es menor), entonces las burbujas de vapor generadas por el líquido comienzan a desplazar al gas que mantenía la presión total, y se dice que la mezcla hierve. Esta temperatura se denomina "punto de ebullición" de la mezcla líquida a la presión dada (se supone que la presión total se mantiene constante ajustando el volumen total del sistema para adaptarse a los cambios de volumen específicos que acompañan a la ebullición). El punto de ebullición a una presión global de 1 atm se denomina "punto de ebullición normal" de la mezcla líquida.
Descripción termodinámica del equilibrio vapor-líquido[editar]
El campo de la termodinámica describe cuándo es posible el equilibrio vapor-líquido, y sus propiedades. Gran parte del análisis depende de si el vapor y el líquido consisten en un solo componente, o si son mezclas.
Sistemas puros (monocomponentes)[editar]
Si el líquido y el vapor son puros, en el sentido de que están formados por un solo componente molecular y sin impurezas, entonces el estado de equilibrio entre las dos fases se describe mediante las siguientes ecuaciones:
- ;
- ; and
donde y son las presiones dentro del líquido y vapor, and son las temperaturas dentro del líquido y el vapor, y y son las energías de Gibbs molares (unidades de energía por cantidad de sustancia) dentro del líquido y el vapor, respectivamente.[4] En otras palabras, la temperatura, la presión y la energía libre de Gibbs molar son las mismas en cada una de las dos fases cuando están en equilibrio.
Una forma equivalente y más común de expresar la condición de equilibrio vapor-líquido en un sistema puro es usando el concepto de fugacidad. Bajo este punto de vista, el equilibrio se describe mediante la siguiente ecuación:
donde y son las fugacidades del líquido y del vapor, respectivamente, a la temperatura del sistema Ts y a la presión Ps.[5] El uso de la fugacidad es a menudo más conveniente para el cálculo, dado que la fugacidad del líquido es, con una buena aproximación, independiente de la presión,[6] y a menudo es conveniente usar la cantidad , el "coeficiente de fugacidad" sin dimensiones, que es 1 para un gas ideal.
Sistemas multicomponentes en equilibrio líquido-vapor[editar]
En un sistema multicomponente, donde el vapor y el líquido consisten en más de un tipo de compuestos, describir el estado de equilibrio es más complicado. Para todos los componentes i del sistema, el estado de equilibrio entre las dos fases se describe mediante las siguientes ecuaciones:
- ;
- ; and
donde P y T son la temperatura y la presión para cada fase, y y son las magnitudes molares parciales también llamadas potencial químico. (unidades de energía por cantidad de sustancia) dentro del líquido y vapor, respectivamente, para cada fase. El molar parcial de energía libre de Gibbs se define por:
donde G es la (extensiva) energía libre de Gibbs, y ni es la cantidad de sustancia de componente i.
Diagramas del punto de ebullición[editar]
Los datos de la mezcla binaria VLE a una cierta presión global, como 1 atm, que muestran las concentraciones de vapor y líquido de la fracción molar al hervir a varias temperaturas, pueden mostrarse como un gráfico] bidimensional llamadodiagrama de punto de ebullición. La fracción molar del componente 1 en la mezcla puede representarse con el símbolo x1. La fracción molar del componente 2, representada por x2, está relacionada con x1 en una mezcla binaria como sigue:
- x1 + x2 = 1
En mezclas multicomponentes en general con componentes N, esto se convierte en:
- x1 + x2 + ... + xn = 1

Las ecuaciones de equilibrio precedentes se aplican típicamente para cada fase (líquida o vapor) individualmente, pero el resultado puede ser graficado en un solo diagrama. En un diagrama binario del punto de ebullición, la temperatura (T ) se representa en función de x1. A cualquier temperatura dada donde ambas fases están presentes, el vapor con una cierta fracción molar está en equilibrio con el líquido con una cierta fracción molar. Las dos fracciones molares a menudo difieren. Estas fracciones de vapor y líquido están representadas por dos puntos en la misma línea isotérmica horizontal (constante T ). Cuando se grafica un rango completo de temperaturas en comparación con las fracciones molares de vapor y líquido, se obtienen dos líneas (generalmente curvas). La inferior, que representa la fracción molar del líquido en ebullición a distintas temperaturas, se denomina curva punto de burbuja. La superior, que representa la fracción molar del vapor a diversas temperaturas, se denomina curva del punto de rocío.[1]
Estas dos curvas se encuentran necesariamente cuando la mezcla se convierte en un solo componente, es decir, cuando x1 = 0. (y x2 = 1, componente puro 2) o x1 = 1. (y x2 = 0, componente puro). Las temperaturas en esos dos puntos corresponden a los puntos de ebullición de cada uno de los dos componentes puros.
Para ciertos pares de sustancias, las dos curvas también coinciden en algún momento estrictamente entre x1 = 0 y x1 = 1. Cuando se encuentran, se encuentran tangencialmente; la temperatura del punto de rocío siempre está por encima de la temperatura del punto de ebullición para una composición dada cuando no son iguales. El punto de encuentro se llama un azeótropo para ese par de sustancias en particular. Se caracteriza por una temperatura azeotrópica y una composición azeotrópica, a menudo expresada como una fracción molar. Puede haber azeotrópicos de ebullición máxima, donde la temperatura de los azeotrópicos es máxima en las curvas de ebullición, o azeotrópicos de ebullición mínima, donde la temperatura de los azeotrópicos es mínima en las curvas de ebullición.
Si se desea representar un dato VLE para una mezcla de tres componentes como "diagrama" de punto de ebullición, se puede utilizar un gráfico tridimensional. Dos de las dimensiones se utilizarían para representar las fracciones molares de la composición, y la tercera dimensión sería la temperatura. Utilizando dos dimensiones, la composición puede representarse como un triángulo equilátero en el que cada esquina representa uno de los componentes puros. Los bordes del triángulo representan una mezcla de los dos componentes en cada extremo del borde. Cualquier punto dentro del triángulo representa la composición de una mezcla de los tres componentes. La fracción molar de cada componente correspondería al punto en el que se encuentra un punto a lo largo de una línea que comienza en la esquina de ese componente y es perpendicular al borde opuesto. Los datos punto de burbuja y punto de rocío se convertirían en superficies curvas dentro de un prisma triangular, que conecta los tres puntos de ebullición en los "ejes" verticales de temperatura. Cada cara de este prisma triangular representaría un diagrama de punto de ebullición bidimensional para la mezcla binaria correspondiente. Debido a su complejidad tridimensional, estos diagramas de punto de ebullición son raramente vistos. Alternativamente, las superficies curvas tridimensionales pueden representarse en un gráfico bidimensional mediante el uso de líneas isotérmicas curvas a intervalos graduados, similares a las líneas de iso-altitud de un mapa. Se necesitan dos conjuntos de estas líneas isotérmicas en un gráfico bidimensional de este tipo: un conjunto para la superficie del punto de burbuja y otro para la superficie del punto de rocío.
K y valores de volatilidad relativa[editar]

La tendencia de una determinada especie química a dividirse a sí misma preferentemente entre las fases líquida y vapor es la constante la ley de Henry. Puede haber datos VLE para mezclas de cuatro o más componentes, pero un diagrama de punto de ebullición de este tipo es difícil de mostrar en forma tabular o gráfica. Para tales mezclas multicomponentes, así como para mezclas binarias los datos de equilibrio vapor-líquido se representan en términos de valores de K (ratio de distribución vapor-líquido)[1][2] definido por
donde yi y xi son las fracciones molares del componente i en las fases y y x respectivamente.
Para la ley de Raoult
Para la modificado ley de Raoult
donde es el coeficiente de actividad, Pi es la presión parcial y P es la presión.
Los valores de la relación Ki están correlacionados empírica o teóricamente en términos de temperatura, presión y composiciones de fase en forma de ecuaciones, tablas o gráficos como las tablas DePriester (mostradas a la derecha).[7]


En el caso de las mezclas binarias, la relación de los valores K para los dos componentes se denomina volatilidad relativa denotada por α.
que es una medida de la relativa facilidad o dificultad de separar los dos componentes. La destilación industrial a gran escala rara vez se realiza si la volatilidad relativa es inferior a 1,05, siendo el componente volátil i y el componente menos volátil j.[2]
Los valores de K se utilizan ampliamente en los cálculos de diseño de columnas destilación continua para destilar mezclas multicomponentes.
Diagramas de equilibrio vapor-líquido[editar]
Para cada componente de una mezcla binaria, se podría hacer un diagrama de equilibrio vapor-líquido. Dicho diagrama representaría gráficamente la fracción molar líquida en un eje horizontal y la fracción molar de vapor en un eje vertical. En dichos diagramas VLE, las fracciones molares líquidas para los componentes 1 y 2 pueden representarse como x1 y x2 respectivamente, y las fracciones molares de vapor de los componentes correspondientes suelen representarse comoy1 y y2.[2] Similarmente para mezclas binarias en estos diagramas VLE:
- x1 + x2 = 1 and y1 + y2 = 1.
Estos diagramas VLE son cuadrados con una línea diagonal que va desde la esquina (x1 = 0, y1 = 0) hasta la esquina (x1 = 1, y1 = 1) como referencia.
Estos tipos de diagramas VLE se utilizan en el método de McCabe-Thiele para determinar el número de etapas de equilibrio (o placa teóricas) necesarias para destilar una determinada composición de una mezcla binaria de alimentación en una fracción de destilado y una fracción de fondo. También se pueden hacer correcciones para tener en cuenta la eficiencia incompleta de cada bandeja en una columna de destilación en comparación con una placa teórica.
Ley de Raoult[editar]
A temperaturas de ebullición y superiores, la suma de las presiones parciales de cada componente es igual a la presión total, que puede simbolizarse como Ptot.
Bajo tales condiciones, la ley de Dalton estaría en efecto como sigue:
- Ptot = P1 + P2 + ...
Luego, para cada componente en la fase de vapor:
- y1 = P1 / Ptot, y2 = P2 / Ptot, ... etc.
donde P1 = presión parcial del componente 1, P2 = presión parcial del componente 2, etc.".
La ley de Raoult es aproximadamente válido para mezclas de componentes entre los cuales hay muy poca interacción aparte del efecto de la dilución por los otros componentes. Ejemplos de tales mezclas incluyen mezclas de alcanos, que no sonpolar, relativamente inertes compuestos en muchos sentidos, por lo que hay poca atracción o repulsión entre las moléculas. La ley de Raoult establece que para los componentes 1, 2, etc. en una mezcla:
- P1 = x1 P o1, P2 = x2 P o2, ... etc.
donde P o1, P o2, etc. son las presiones de vapor de los componentes 1, 2, etc. cuando son puros, y x1, x2, etc. son fracciones molares del componente correspondiente en el líquido.
Recordemos de la primera sección que las presiones de vapor de los líquidos son muy dependientes de la temperatura. Así pues, las presiones de vapor puro Po para cada componente son una función de la temperatura (T). Por ejemplo, comúnmente para un componente líquido puro, la relación Clausius-Clapeyron puede usarse para aproximar cómo varía la presión de vapor en función de la temperatura. Esto hace que cada una de las presiones parciales dependa de la temperatura, independientemente de si se aplica o no la ley de Raoult. Cuando la ley de Raoult es válida, estas expresiones se convierten en:
- P1T = x1 P o1T, P2T = x2 P o2T, ... etc.
A temperaturas de ebullición, si se aplica la ley de Raoult, la presión total se convierte en:
- Ptot = x1 P o1T + x2 P o2T + ... etc.
En un determinado Ptot como 1 atm y una determinada composición líquida, T puede resolverse para dar el punto de ebullición o punto de burbuja de la mezcla líquida, aunque la solución para T puede no ser matemáticamente analítica (es decir, puede requerir una solución numérica o una aproximación). Para una mezcla binaria en un determinado Ptot, el punto de burbuja T puede convertirse en una función de x1 (or x2) y esta función puede mostrarse en un gráfico bidimensional como un diagrama de punto de ebullición binario.
A temperaturas de ebullición, si se aplica la ley de Raoult, se pueden combinar varias de las ecuaciones anteriores en esta sección para dar las siguientes expresiones para las fracciones molares de vapor en función de las fracciones molares líquidas y la temperatura:
- y1 = x1 P o1T / Ptot, y2 = x2 P o2T / Ptot, ... etc.
Una vez determinado el punto de burbuja T's en función de la composición del líquido en términos de fracciones molares, estos valores pueden insertarse en las ecuaciones anteriores para obtener las correspondientes composiciones de vapor en términos de fracciones molares. Cuando esto se termina en un rango completo de fracciones molares líquidas y sus correspondientes temperaturas, se obtiene efectivamente una función T de fracciones molares con composición de vapor. Esta función actúa efectivamente como el punto de rocío T función de la composición de vapor.
En el caso de una mezcla binaria, x2 = 1 − x1 y las ecuaciones anteriores pueden expresarse como:
- y1 = x1 P o1T / Ptot, and
- y2 = (1 − x1) P o2T / Ptot
Para muchos tipos de mezclas, particularmente cuando hay interacción entre componentes más allá de los efectos de la dilución, la ley de Raoult no funciona bien para determinar las formas de las curvas en el punto de ebullición o en los diagramas VLE. Incluso en tales mezclas, por lo general todavía existen diferencias en las concentraciones de equilibrio de vapor y líquido en la mayoría de los puntos, y la destilación a menudo sigue siendo útil para separar los componentes al menos parcialmente.
Para tales mezclas, los datos empíricos se utilizan típicamente para determinar el punto de ebullición y los diagramas VLE. Los Ingeniero químico han hecho una cantidad significativa de investigación tratando de desarrollar ecuaciones para correlacionar y/o predecir datos VLE para varios tipos de mezclas que no obedecen bien a la ley de Raoult.
Véase también[editar]
| Destilación | |
|---|---|
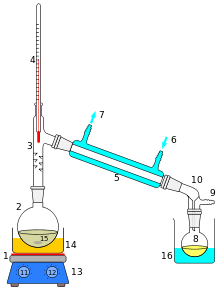
| |
| Ramas | |
| Ley de Raoult / Ley de Dalton / Reflujo / Ecuación de Fenske / Método de McCabe-Thiele / Plato teórico / Presión parcial / Equilibrio vapor-líquido | |
| Procesos industriales | |
| Métodos de laboratorio | |
| Técnicas | |
- Destilación continua
- Base de datos de Dortmund (incluye una colección de datos VLE)
- Ecuación de Fenske
- Destilación flash
- Modelo DECHEMA
- Caldera manual
- Ecuación de Van Laar
- Modelo de actividad de Margules
- Pervaporación
- Sobrefusión
- Vapor sobrecalentado
Enlaces externos[editar]
- Distillation Principals por Ming T. Tham, University of Newcastle upon Tyne (véase abajo para Volatilidad Relativa)
- Introduction to Distillation: Vapor Liquid Equilibria
- VLE Thermodynamics (Departamento de Ingeniería Química, Prof. Richard Rowley, Universidad Brigham Young)* NIST Standard Reference Database 103b (Describe la extensa base de datos VLE disponible en NIST)
- Some VLE data sets and diagrams for mixtures of 30 common components, un pequeño subconjunto del Banco de Datos de Dortmund.
- Where can I get the vapor-liquid phase equilibrium data? Archivado el 3 de febrero de 2018 en Wayback Machine. Referencia a las diversas fuentes de datos de equilibrio de fase
- Can. J. Chem. Eng. ternary and multicomponent systems from binary ones
- George Schlowsky, Alan Erickson y Thomas A. Schafer, Modular Process Systems, Inc.[https://web.archive.org/web/20151208081630/http://modularprocess.com/wp-content/uploads/2015/07/Article-GeneratingYourOwnVLE-ChE-1995.pdf Operations & Maintenance - Generating your own VLE Data, Ingeniería Química, marzo de 1995, McGraw-Hill, Inc.
- Esta obra contiene una traducción derivada de «Vapor-liquid equilibrium» de Wikipedia en inglés, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
Referencias[editar]
- ↑ a b c Kister, Henry Z. (1992). Distillation Design (1st edición). McGraw-hill. ISBN 0-07-034909-6.
- ↑ a b c d Perry, R.H.; Green, D.W., eds. (1997). Perry's Chemical Engineers' Handbook (7th edición). McGraw-hill. ISBN 0-07-049841-5.
- ↑ Seader, J. D.; Henley, Ernest J. (1998). Separation Process Principles. New York: Wiley. ISBN 0-471-58626-9.
- ↑ Balzhiser et al. (1972), Chemical Engineering Thermodynamics, p. 215.
- ↑ Balzhiser et al. (1972), "Chemical Engineering Thermodynamics", p.216.
- ↑ Balzhiser et al. (1972), Chemical Engineering Thermodynamics, p.218.
- ↑ DePriester, C.L., Chem. Eng. Prog. Symposium Series, 7, 49, páginas 1-43






















