Cónica generalizada

En matemáticas, una cónica generalizada es un objeto geométrico definido por una propiedad que es una generalización de alguna de las propiedades definitorias de una sección cónica clásica.

Visión general

Una elipse puede definirse como el lugar geométrico de los puntos de un plano tales que la suma de sus distancias desde dos puntos fijos también del mismo plano (sus focos) es constante. La curva obtenida cuando el conjunto de dos puntos fijos es reemplazado por un conjunto finito arbitrario, pero fijo, de puntos en el plano se denomina n–elipse y puede considerarse como una elipse generalizada. Como una elipse es el conjunto equidistante de dos círculos, el conjunto equidistante de dos conjuntos arbitrarios de puntos en un plano se puede ver como una cónica generalizada.

En coordenadas cartesianas rectangulares, la ecuación y = x² representa una parábola. La ecuación generalizada y = x ^r, para r ≠ 0 y r ≠ 1, se puede tratar como la definición de una parábola generalizada. La idea de la cónica generalizada ha encontrado aplicaciones en la teoría de la aproximación y en procesos de optimización.​

Entre las varias formas posibles en que el concepto de una cónica se puede generalizar, el enfoque más utilizado es definirla como una generalización de la elipse. El punto de partida para este enfoque es considerar una elipse como una curva que satisface la "propiedad de dos focos": una elipse es una curva que es el lugar geométrico de los puntos cuya suma de distancias a dos puntos dados es constante. Los dos puntos son los focos de la elipse. La curva obtenida reemplazando el conjunto de dos puntos fijos por un conjunto finito arbitrario, pero fijo, de puntos en el plano se puede considerar como una elipse generalizada. Las cónicas generalizadas con tres focos se llaman elipses trifocales.

Esto se puede generalizar adicionalmente a las curvas que se obtienen como los lugares geométricos de los puntos que se sitúan de manera tal que la media ponderada de las distancias desde un conjunto finito de puntos es una constante. Todavía es posible una generalización adicional, suponiendo que los pesos asociados a las distancias pueden ser de signo arbitrario, es decir, positivos o negativos.

Finalmente, también puede eliminarse la restricción de que el conjunto de puntos fijos, llamado conjunto de focos de la cónica generalizada, sea finito. Se puede suponer que el conjunto es finito o infinito. En el caso infinito, la media aritmética ponderada tiene que ser reemplazada por una integral apropiada. Las cónicas generalizadas en este sentido también se llaman polielipses, ovoelipses o elipses generalizadas. Dado que dichas curvas fueron estudiadas por el matemático alemán Ehrenfried Walther von Tschirnhaus (1651-1708) también se las conoce como óvalos de Tschirnhaus.​ Dichas generalizaciones también fueron analizadas por René Descartes​ y por James Clerk Maxwell.​

Curvas ovales multifocales

Construcción del óvalo definido por AP + 2BP = c utilizando alfileres, lápiz y una cuerda, descrita por James Clerk Maxwell.

Construcción del óvalo definido por AP + BP + CP = c utilizando alfileres, lápiz y una cuerda, descrita por James Clerk Maxwell.

René Descartes (1596-1650), padre de la geometría analítica, en su obra La Geometrie publicada en 1637, dedicó una sección de aproximadamente 15 páginas para analizar lo que él había llamado elipses bifocales. Definió un óvalo bifocal como el lugar geométrico de un punto P que se mueve en un plano tal que $AP+\lambda BP=c$ donde A y B son puntos fijos en el plano y λ y c son constantes que pueden ser positivas o negativas. Descartes había introducido estos óvalos, que ahora se conocen como óvalos cartesianos, para determinar las superficies de una lente de modo que los rayos se encuentren en el mismo punto tras refractarse. Descartes también había identificado estos óvalos como generalizaciones de las cónicas centrales, porque para ciertos valores de λ estos óvalos se reducen a las cónicas centrales familiares, a saber, el círculo, la elipse o la hipérbola.​

Los óvalos multifocales fueron redescubiertos por James Clerk Maxwell (1831-1879) cuando todavía era un estudiante de escuela. A la temprana edad de 15 años, Maxwell escribió un artículo científico sobre estos óvalos con el título "Observaciones sobre figuras circunscriptas que tienen una pluralidad de focos y radios de varias proporciones" y se lo presentó al profesor J.D. Forbes en una reunión de la Royal Society de Edimburgo en 1846. El profesor J.D. Forbes también publicó un informe sobre el documento en las Actas de la citada sociedad.​​ En su artículo, aunque Maxwell no utilizó el término "cónica generalizada", estaba considerando curvas definidas por condiciones que fueron generalizaciones de la condición definitoria de una elipse.

Definición

Un óvalo multifocal es una curva que se define como el lugar geométrico de un punto que se mueve de tal manera que

$\lambda _{1}A_{1}P+\lambda _{2}A_{2}P+\cdots +\lambda _{n}A_{n}P=c$

donde A₁, A₂,. . . , A_n son puntos fijos en un plano y λ₁, λ₂,. . . , λ_n son números racionales fijos y c es una constante. Maxwell ideó métodos simples utilizando alfileres, lápiz y una cuerda para dibujar tales óvalos.

El método para dibujar el óvalo definido por la ecuación $AP+2BP=c$ ilustra el enfoque general adoptado por Maxwell para representar tales curvas:

• Fíjense dos alfileres en los focos A y B.
• Tómese una cuerda cuya longitud sea c + AB.
• Átese un extremo de la cuerda al alfiler situado en A .
• Se une el lápiz al otro extremo de la cuerda y la cuerda se pasa alrededor del alfiler en el foco B.
• El lápiz se mueve guiado por la cuerda tensa recorriendo la propia cuerda (véase el dibujo).
• La curva trazada por el lápiz es el lugar geométrico de P.

Su disposición es más evidente en su descripción del método para dibujar un óvalo trifocal definido por una ecuación de la forma $AP+BP+CP=c$:

• Fíjense tres alfileres en los tres focos A, B y C.
• Fijar un extremo de la cuerda en el alfiler situado en C.
• Pasar la cuerda alrededor de los otros dos alfileres.
• Unir el lápiz al otro extremo de la cuerda.
• Pasar el lápiz por A y C, y tensar hasta alcanzar P, moviéndolo de forma que la cuerda quede tensa.

La figura resultante sería un sector de una elipse trifocal. Las posiciones de la cuerda pueden tener que ajustarse para obtener el óvalo completo.

En los dos años posteriores a la presentación de su trabajo en la Royal Society de Edinburgo, Maxwell desarrolló sistemáticamente las propiedades geométricas y ópticas de estos óvalos.​

Especialización y generalización del enfoque de Maxwell

Como un caso especial del enfoque de Maxwell, considérese la n-elipse, el lugar geométrico de un punto que se mueve de tal manera que se cumple la siguiente condición:

$A_{1}P+A_{2}P+\cdots +A_{n}P=c.\,$

Dividiendo por n y reemplazando c/n por c, esta condición definitoria se puede expresar como

${\frac {1}{n}}(A_{1}P+A_{2}P+\cdots +A_{n}P)=c$

Esto sugiere una interpretación simple: la cónica generalizada es una curva tal que la distancia promedio de cada punto P en la curva del conjunto {A₁, A₂,. . . , A_n} tiene el mismo valor constante. Esta formulación del concepto de cónica generalizada se ha ampliado aún más de varias maneras diferentes.

• Modificación de la definición del promedio. En la formulación, el promedio se interpretó como la media aritmética. Esto puede ser reemplazado por otras nociones de promedios como la media geométrica de las distancias. Si la media geométrica se usa para especificar el promedio, las curvas resultantes resultan ser lemniscatas, conjuntos cuyos puntos tienen la misma media geométrica de las distancias (es decir, su producto es constante). Las lemniscatas desempeñan un papel central en la teoría de la aproximación. La aproximación polinómica de una función holomórfica se puede interpretar como la aproximación de curvas de nivel con lemniscatas. El producto de las distancias corresponde al valor absoluto de la descomposición de las raíces de los polinomios en el plano complejo.​
• Modificación del cardinal del conjunto focal. La definición se puede modificar para que se pueda aplicar incluso en el caso en el que el conjunto focal sea infinito. Esta posibilidad fue presentada por primera vez por C. Gross y T.-K. Strempel, que plantearon el problema de si los resultados (del caso clásico) pueden extenderse al caso de infinitos puntos focales o a un conjunto continuo de focos.​
• Cambiar la dimensión del espacio subyacente. Se puede suponer que los puntos se encuentran en algún espacio d-dimensional.
• Cambiar la definición de la distancia. Tradicionalmente se emplean definiciones euclidianas. En su lugar, se pueden usar otras nociones de distancia como la distancia del taxista.​​ Las cónicas generalizadas con esta noción de distancia han encontrado aplicaciones geométricas en tomografía.​​

La formulación de la definición de una cónica generalizada en el caso más general, cuando la cardinalidad del conjunto focal es infinita, implica las nociones de conjuntos medibles e integración de Lebesgue. Todos estos supuestos han sido analizados por diferentes autores y las curvas resultantes han sido estudiadas con especial énfasis en sus aplicaciones.

Definición

Sea $d:R^{n}\rightarrow R$ un espacio métrico y $\mu$ una medida en un conjunto compacto $K\subset R^{n}$ con $\mu (K)>0$. La función cónica generalizada no ponderada $f_{K}$ asociada con $K$ es

$f_{K}(x)=\int _{K}g(x,y)d(x,y)\,d_{\mu }y$

donde $g:R^{n}\times R^{n}\rightarrow R$ es una función central asociada con $f_{K}$. $K$ es el conjunto de focos. Los conjuntos de niveles $\{x\in R^{n}:f_{K}(x)<c\}$ se llaman generalizados.​

Cónicas generalizadas mediante ecuaciones polares

La figura muestra la posición inicial de un cono circular recto, junto con una sección plana, antes de desarrollarlo sobre un plano.

La figura muestra una posición arbitraria de un cono circular recto, junto con una sección plana, mientras el cono se desarrolla sobre un plano. La figura también muestra la cónica generalizada (curva punteada sobre el plano) que representa el desarrollo de la sección cónica inscrita en el cono sobre el plano.

Dada una cónica, al elegir un foco de la cónica como polo y la línea a través del polo dibujado en paralelo a la directriz de la cónica como eje polar, las coordenadas polares de la sección cónica se pueden escribir de la siguiente forma:

$r={\frac {ed}{1+e\sin \theta }}$

Aquí e es la excentricidad de la cónica y d es la distancia de la directriz desde el polo. Tom Mike Apostol y Mamikon A. Mnatsakanian en su estudio de curvas dibujadas en las superficies de conos circulares rectos introdujeron una nueva clase de curvas que denominaron cónicas generalizadas.​​ Son curvas cuyas ecuaciones polares son similares a las ecuaciones polares de las cónicas comunes y las cónicas ordinarias aparecen como casos especiales de estas cónicas generalizadas.

Definición

Para las constantes reales r₀ ≥ 0, λ ≥ 0 y k, una curva plana descrita por la ecuación polar

$r={\frac {r_{0}}{1+\lambda \sin(k\theta )}}$

se llama cónica generalizada.​ La cónica se denomina elipse, parábola o hipérbola generalizada según λ < 1, λ = 1 o λ > 1.

Casos especiales

• En el caso especial cuando k = 1, la cónica generalizada se reduce a una cónica ordinaria.
• En el caso especial cuando k > 1, existe un método geométrico simple para la generación de la correspondiente cónica generalizada.​

Sea α un ángulo tal que: $\sin \alpha =1/k$. Considérese un cono circular recto con un semiángulo respecto a la vertical igual a α. Considérese la intersección de este cono por un plano tal que la intersección sea una cónica con excentricidad λ. Desarróllese el cono sobre un plano. Entonces, la curva en el plano sobre el que se desarrolla la sección cónica de excentricidad λ es una cónica generalizada con ecuación polar como se especifica en la definición.

• En el caso especial cuando k < 1, la cónica generalizada no puede obtenerse al desarrollar una sección cónica. En este caso, hay otra interpretación.

Considérese una cónica ordinaria dibujada sobre un plano. Envuélvase el plano para formar un cono circular recto, de forma que la cónica se convierta en una curva en el espacio tridimensional. La proyección de la curva en un plano perpendicular al eje del cono será una cónica generalizada en el sentido de Apostol y Mnatsakanian con k < 1.

Ejemplos

r0 = 5, λ = 0.6, k = 1.5	r0 = 5, λ = 0.22, k = 5.5	r0 = 5, λ = 1, k = 1.5	r0 = 5, λ = 1, k = 1.15
r0 = 5, λ = 1.6, k = 1.5	r0 = 5, λ = 0.8, k = 0.5	r0 = 5, λ = 1.0, k = 0.5	r0 = 5, λ = 1.5, k = 0.5

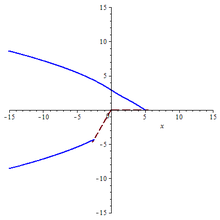Cónicas generalizadas en aproximaciones de curvas

En 1996, Ruibin Qu introdujo una nueva noción de cónica generalizada como herramienta para generar aproximaciones a otras curvas.​ El punto de partida para esta generalización es el resultado de que la secuencia de puntos $\{P_{k}:k=0,1,2,\ldots \}$ definida por

$P_{k+1}=2\alpha P_{k}-P_{k-1}$

se sitúa sobre una cónica. Con este enfoque, las cónicas generalizadas se definen como sigue.

Definición

Una cónica generalizada es una curva tal que si los dos puntos $P_{0}$ y $P_{1}$ están en ella, entonces los puntos $\{P_{k}:k>1\}$ generados por la relación recursiva

$P_{k+1}=2\alpha P_{k}+\beta P_{k-1}$

para algunos $\alpha$ y $\beta$ que satisfacen las relaciones

$\alpha \beta \neq 0,\quad (\alpha ,\beta )\neq (\pm 1,-1),\quad \alpha ^{2}+\beta \neq 0$

también están en ella.

Cónicas generalizadas como conjuntos equidistantes

Animación que muestra la generación de una 'elipse' como el conjunto equidistante de dos circunferencias.

Definición

Sea (X, d) un espacio métrico, y A un subconjunto no vacío de X. Si x es un punto en X, la distancia entre x y A se define como d (x, A) = inf {d (x, a): a en A}. Si A y B son subconjuntos no vacíos de X, entonces el conjunto equidistante determinado por A y B se define como el conjunto {x en X:d(x, A) = d(x, B)}. Este conjunto equidistante se denota por {A = B}. El término cónica generalizada se usa para denotar un conjunto equidistante general.​

Ejemplos

Las cónicas clásicas se pueden interpretar como conjuntos equidistantes. Por ejemplo, si A es un punto único y B es una línea recta, entonces el conjunto equidistante {A = B} es una parábola. Si A y B son círculos tales que A está completamente dentro de B, entonces el conjunto equidistante {A = B} es una elipse. Por otro lado, si A se encuentra completamente fuera de B, el conjunto equidistante {A = B} es una hipérbola.

Lecturas adicionales

• Para una discusión detallada de las cónicas generalizadas desde el punto de vista de la geometría diferencial, consúltese el capítulo sobre cónicas generalizadas en el libro Convex Geometry de Csaba Vincze disponible en línea.​

• Datos: Q25304533
• Multimedia: Generalized conic / Q25304533