Algoritmo de Bresenham

Ejemplo de aplicación del algoritmo de Bresenham.

El Algoritmo de Bresenham es un método rápido para el trazado de líneas en dispositivos gráficos, cuya cualidad más apreciada es que solo realiza cálculos con enteros.

Se puede adaptar para rasterizar también circunferencias y curvas. Los ejes verticales muestran las posiciones de rastreo y los ejes horizontales identifican columnas de pixel.

Actualmente se usa el nombre de algoritmos de Bresenham a toda una familia de algoritmos basado en modificaciones o ampliaciones del original aquí descrito.

Introducción

El trazador rotatorio Calcomp 565.

El algoritmo inicialmente fue desarrollado por Jack Elton Bresenham al comienzo del verano de 1962, para dibujar sobre un plóter de Calcomp, operado desde un IBM. Por aquella época era común compartir libremente los programas, y en la empresa era normal que otros compañeros dispusieran de copias. No fue el propio Bresenham quien publicó su algoritmo, sino otros que le pidieron permiso para presentarlo en su nombre en la convención nacional de ACM, en Denver (Colorado) en 1963. Y en 1965 fue impreso por vez primera.

Cabe señalar que los plóter de Calcomp, fueron de los primeros dispositivos con salida gráfica a la venta, allá por 1959.

El algoritmo, finalmente ha encontrado un uso masivo en los gráficos de ordenador, debido a su velocidad y sencillez. También es notable la no necesidad de una unidad de coma flotante para realizar los cálculos necesarios.

Problemática del trazado de las líneas rectas

Al trazar una línea recta sobre papel con un lápiz, no existen impedimentos para colocar una regla y seguir una línea completamente recta.

En cambio cuando se opera sobre un sistema mapeado (como es la propia representación pixelada) en filas y columnas (cuadriculado), una línea siempre seguirá un trazado imperfecto, ya que la propia línea imaginaria trazada entre dos puntos, (excepto para las líneas horizontales y verticales), siempre cortará los cuadrados por donde pase, dividiendo al punto mínimo en dos áreas de diferente tamaño.

Sobre una rejilla de 7x11, se observa la línea ideal trazada en rojo, se perciben los errores al seguir las líneas en verde. Los cuadros marcados en amarillo, serían una posible solución de la línea.

Es decir el trazado de una línea sobre un soporte mapeado donde forzosamente debe ocuparse como unidad mínima un cuadro del mapa como equivalente de un punto siempre será una aproximación de la línea ideal y por tanto siempre contiene errores. Errores que son la consecuencia del paso de valores continuos a valores discretos, el paso de lo analógico a lo digital.

La aproximación del dibujado de los puntos que describen la línea presenta dos claros problemas:

• Qué puntos pasan por la recta (en lo sucesivo, diremos píxeles).
• De los puntos que pasen por la recta, cuáles deben dibujarse.

Qué puntos pasan por la recta

Dados dos puntos que describen el punto inicial y final de la recta, se conoce las medidas básicas de la línea, ancho y alto que abarca la línea.

Un modo sencillo de saber cuáles pasan por la línea consiste en dividir una medida entre la otra. Por ejemplo si la línea queda descrita por los dos siguientes puntos coordenados: G3-C9 restando el valor inicial, del valor final para cada dimensión, obtenemos las medidas en dichas dimensiones respectivamente. Sobre el eje vertical tendremos: C-G = -4 y sobre el eje horizontal tendremos: 9-3 = 6

Ahora sabremos que por cada punto que avance sobre la vertical debe avanzar 1'5 sobre la horizontal. Aunque 1'5 sea una medida cómoda, trabajar con decimales cuando operamos sobre unidades enteras, es parte del problema.

Cuáles se deben dibujar

Es evidente que en función del grosor de la línea, tocará a más o menos píxeles a lo largo de la misma. Supongamos que la línea ideal es mucho más fina que la unidad del punto (píxel).

La solución para cuáles dibujar, podría optarse por iluminar cada píxel que toca al trazarse la línea ideal, también podría optarse por iluminar aquellos píxeles que queden cortados por un determinado porcentaje del área de cada píxel (al que se le ha supuesto idealizado como una caja mucho mayor que el grosor de la línea ideal).

Con base en dicho porcentaje, pueden darse diferentes artefactos... si la línea pasa muy cerca de la esquina donde se tocan 4 píxeles, podrían quedar huecos en la línea si no se dibujan, o quedar muy ancha la línea si ven.

Estado del arte previo

El problema existe desde la afamada cuadratura del círculo (que es un problema clásico de geometría), pero en este artículo nos ceñimos exclusivamente a la problemática gráfica.

Hasta la fecha aunque se trabajaba con cuadrículas, los trazados solían hacerse con maquinaria analógica, por lo que los trazados, simplemente solían discurrir los límites que un brazo mecánico permitía, ya fueran estos límites líneas rectas o curvas y que en su movimiento arrastraban algún tipo de pincel, o un sistema impulsado que escupe la pintura o tinta.

El algoritmo de Bresenham, por tanto encabeza los algoritmos para el dibujado en los llamados gráficos vectoriales, que requieren básicamente líneas y arcos.

Descripción

Antes de entrar en detalles de su descripción entramos en algunas consideraciones que servirán para entender con facilidad el porqué de cada cosa del algoritmo.

Consideraciones previas

Trazado de una simple línea sobre un octante, reflejando la línea ideal y la línea que se obtiene con el algoritmo.

Dados dos puntos y obtenido la distancia en el eje vertical y horizontal que los separa, se utilizan dichos valores para sobre uno de los ejes suponer un bucle de avance unitario y sobre el otro eje, preparar otro bucle anidado dentro del primero y cuyo avance es relativo, esto es, a veces avanza una unidad y a veces no.

Conviene también entender que la línea puede tener cualquier orientación. Al caso conviene considerar un círculo e imaginar el centro como el punto inicial. Y el punto final, considerar situarlo en cualquier punto que pase por la línea del círculo. Es decir estamos definiendo para cualquier línea así trazada un radio idéntico, pero que en función del ángulo descrito por la línea trazada (o a trazar) respecto de la normal varían en ancho y alto.

Una vez considerado el círculo, se observa que básicamente puede ser subdividido en octantes (8 partes iguales). Basándonos en que para cada octante, la medida vertical es menor o igual que la horizontal, más las consideraciones de valores positivos y negativos para cada eje (2x4=8 posibilidades). Resumiendo todas las líneas caen en una de 8 posibilidades distinta (aparte del punto, cuando ambos puntos ocupan la misma posición). Véase dichas características en la imagen adjunta más abajo.

Una última consideración, es que los valores de las medidas de ancho o alto, pueden ser:

• Mayor que 0.
• De valor 0.
• Menor que 0.

Descripción del algoritmo

Bresenham, no realizó una descripción clara del algoritmo, sino tan solo dejó comentarios sobre el código máquina que escribió y dado lo peculiar de dicho lenguaje hace difícil de interpretar correctamente sin un conocimiento expreso del mismo. Por lo que la descripción que procede es la interpretación del código y ampliado a una generalización para todos los octantes.

Es probable que no alcance la explicación para terminar de entender por completo el algoritmo, pero con el pseudocódigo y un ejemplo paso a paso, viéndolo operar, se acaba de comprender.

La primera consideración es medir la distancia de la línea para cada eje. Esto es, la distancia que separa ambos puntos que definen los límites de la línea.

Una vez conocida la distancia que se va a recorrer en cada eje, se trata de saber cual de los dos es la medida mayor. Así el eje de mayor medida avanzará siempre una unidad.

El trazado se realiza sobre un bucle, elegido para el eje de mayor medida hallado en el paso previo. Y en cada ciclo (el eje de mayor medida) avanzará siempre una unidad en la dirección hacia el punto final en dicho eje.

En cambio para el otro eje, el avance será a veces una unidad y a veces cero. Esto es, cuando recorra un tramo 'recto' el avance será cero, y cuando recorra un tramo 'inclinado' el avance será una unidad.

Son básicamente dos problemas a resolver:

• Valores de avance según el ángulo de la recta (el octante donde se localiza la línea).
• Avance específico para el eje menor (solución de Bresenham).

Valores de avance según el octante donde cae la línea

Repartición de los octantes alrededor del círculo y asignación de los valores de incremento que los ejes 'x' e 'y', tomarán en cada octante.

Los valores de avance se calculan antes de comenzar el bucle, puesto que ya entonces se conoce cual de las medidas es la de mayor recorrido.

Las menciones al avance de una unidad, tanto para uno como otro eje, también son calculados con anterioridad al bucle una vez conocidas las medidas.

A tales efectos, observando la imagen previa (del círculo con los octantes), se advierte que en función del ángulo que tenga la línea, los valores de incremento (avance) caerán en positivo o negativo tanto para el eje 'x' como al eje 'y'. Al restar el punto final, del punto inicial, obtenemos valores positivos o negativos (o valor 0, que describiría una recta vertical u horizontal, o un punto si ambos valen 0).

Solución de Bresenham para el avance específico del eje menor

Si el bucle itera sobre el eje de mayor medida (ver imagen debajo para determinar esto) con la unidad, es claro que el otro eje, o bien mide lo mismo o menos (incluso 0), luego su avance puede ser 1 o 0 en cada ciclo, esto es 'inclinado' o 'recto', valor de incremento que debe ser actualizado en cada ciclo.

La solución de Bresenham, trata sobre cuando aplicar el avance unitario o cero, para el eje de menor distancia, y es la parte que se describe ahora (la explicación viene dada por comodidad y por simplicidad) para un solo octante donde ambas medidas son positivas, es decir para el octante marcado en la figura como n.º 1 (la numeración de los octantes es arbitraria, puede elegirse indistintamente, según convenga al código si se quieren usar numerados)):

Los 8 octantes en que se subdivide el círculo, se clasifican a su vez en dos grupos. Aquellos en los que cualquier línea trazado en ellos (en el octante), da como resultado que la altura (h) es mayor que la anchura (w) y los que no. Excepto las 4 diagonales donde 'w' y 'h' valen lo mismo.

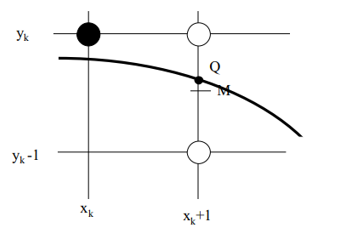
Sean dX y dY la distancias que separan los puntos extremos de la línea sobre cada eje, y 'e' la relación entre el mayor y el menor (e = dX/dY). Entonces, para cada punto se verifica que el eje mayor aumenta 1 y el eje menor 'e'. Pero 'e' es un valor decimal, la decisión de cuando se toma un entero y cuando no, se basa en la acumulación de los decimales, cuando supera uno entero, se dibuja y se resta a dicho valor 1. Si bien esperar a que supere el valor 1, lo aleja del centro ideal de la línea y por ello se toma como valor más cercano al centro, el valor que se acerca en tanta cantidad como se aleja del centro... es decir el valor 0'5.

El valor de 'e' (de la división) no es un entero (salvo caso de una recta o diagonal). Así los valores decimales son considerados como un 'error', que al inicio vale 0 y que luego en cada ciclo se le aumenta el valor de 'e', si el valor de 'error' es superior a 0'5, el valor unitario para el eje menor será en este caso 1, y se resta al 'error' global 1, si no el valor unitario para este ciclo será 0.

Para dejar atrás los valores decimales, se consideran dX y dY sin la división, mediando otros valores que en cada caso de avance unitario suman uno u otro.

En la siguiente imagen (a la derecha) se determina visualmente que todas las líneas que caigan en los octantes rellenados de negro, el eje de mayor media será 'X', las líneas que caigan en los octantes blancos tiene la media del eje 'Y' en mayor medida que para el eje 'X'.

Pseudocódigo del algoritmo

El algoritmo para todos los octantes sería el siguiente:

   Funcion LineaBresenham( X1, Y1, X2, Y2)
      // 0 - Distancias que se desplazan en cada eje
      dY = (Y2 - Y1)
      dX = (X2 - X1)
    
      // 1 - Incrementos para las secciones con avance inclinado
      Si (dY >= 0) entonces
          IncYi = 1
      SiNo
          dY = -dY
          IncYi = -1
      Fin Si
    
      Si (dX >= 0) entonces
          IncXi = 1
      SiNo
          dX = -dX
          IncXi = -1
      Fin Si
    
      // 2 - Incrementos para las secciones con avance recto:
      Si (dX >= dY) entonces
          IncYr = 0
          IncXr = IncXi
      SiNo
          IncXr = 0
          IncYr = IncYi
    
          // Cuando dy es mayor que dx, se intercambian, para reutilizar el mismo bucle.
          // ver octantes blancos en la imagen encima del código
          k = dX: dX = dY: dY = k
      Fin Si
    
      // 3  - Inicializar valores (y de error).
      X = X1: Y = Y1
      avR = (2 * dY)
      av = (avR - dX)
      avI = (av - dX)
    
      // 4  - Bucle para el trazado de las línea.
      Hacer
          DibujarPixel(X, Y, Color) // Como mínimo se dibujará siempre 1 píxel (punto).
          Mensaje(av + " ") // (debug) para ver los valores de error global que van apareciendo.
          Si (av >= 0) entonces
              X = (X + IncXi)     // X aumenta en inclinado.
              Y = (Y + IncYi)     // Y aumenta en inclinado.
              av = (av + avI)     // Avance Inclinado
          SiNo
              X = (X + IncXr)     // X aumenta en recto.
              Y = (Y + IncYr)     // Y aumenta en recto.
              av = (av + avR)     // Avance Recto
          Fin Si
      Repetir hasta que (X = X2) y (Y = Y2) // NOTA: La condición de 'Repetir Hasta' se debe cambiar por (X <> X2) o (Y <> Y2) si se elige en su lugar 'Repetir Mientras'
   Fin funcion

NOTA: Falta añadir imágenes

Seguimiento con un ejemplo

El mejor modo de entender como funciona el algoritmo es servirse de un ejemplo, trazando una línea entre dos puntos, y luego remarcar como va operando el algoritmo.

Algoritmo de Bresenham para el trazado de Circunferencias

Descripción

De primera instancia (García, 2018), inmediatamente menciona que el algoritmo de Bresenham aplicado a una circunferencia se basa en analizar el error entre el verdadero trazo de una circunferencia y su discretización en un plano de píxeles, donde en cada paso el algoritmo elegirá como próximo píxel a aquel que minimice el error, sin embargo de acuerdo con (Weitzenfeld , 2017) para entender completamente el algoritmo aplicado a circunferencias, es necesario partir de conceptos básicos como su definición matemática, hasta su expresión analítica generada de forma discreta dada un punto y su distancia con otro aplicando el teorema de Pitágoras. Así entonces teniendo noción del entorno de trabajo, seremos capaces de incorporar nuevas características al método de estudio, como las coordenadas polares, buscando soluciones que prioricen el grado de complejidad del algoritmo para que este no consuma gran cantidad de recursos, es entonces donde a partir del análisis de errores entre la posición ideal y su posición en el plano de pixeles, el algoritmo será capaz de determinar la correcta posición en único píxel dado el valor con menor índice de error generado a partir de una expresión matemática para la elección de pixeles. Es entonces que enseguida, abordaremos a profundidad cada una de estas etapas mencionadas.

Desarrollo

Matemáticamente una circunferencia será definida como el conjunto de puntos localizados a una distancia r en una posición central representada en el plano x,y. De acuerdo con la geometría analítica y el teorema de Pitágoras la ecuación de la circunferencia queda definida como:

$(x-x_{c})^{2}+(y-y_{c})^{2}=r^{2}$

Conociendo el valor de x, la forma de definir gráficamente la circunferencia se haría a parir de:

$y={\sqrt {r^{2}-(x-x_{c})^{2}}}.$

Trazo para un circulo con radio 10, centrado en (0,0) - Alfredo Weitzenfeld(2017)

(Weitzenfeld , 2017) Menciona que podemos aprovechar esta expresión matemática, tabulando valores discretos de x y que los valores de y serán definidos o redondeados hacia el valor más próximo valor o menor en caso de que estos resulten decimales al aplicar la expresión matemática, además, como forma de optimización, recomienda aprovechar la simetría de los cuatro cuadrantes del plano cartesiano, para el cálculo de la circunferencia total.

Weitzenfeld llama a este un algoritmo básico, ya que tiene bastantes deficiencias, como la cantidad de cálculos considerables que se lleva por cada punto significativo, además de que el espacio entre las posiciones de los píxeles dibujados no es uniforme. Así entonces, hay una propuesta de solución a este problema de trazo de uniformidad, el cual implica el intercambio de los valores entre x y y dada la condición de que el valor absoluto de la pendiente de la circunferencia sea mayor a 1. Sin embargo, anteriormente se comentó que la cantidad de cálculos de este algoritmo básico ya eran muchos, por lo que agregar esta solución hace que aumente la complejidad del algoritmo. Enseguida, la siguiente propuesta a eliminación de los trazos irregulares se basaba en el uso de coordenadas polares a partir de las ecuaciones paramétricas polares de la circunferencia:

$x=x_{c}+r\cos \theta$

$y=y_{c}+r\operatorname {sen} \theta$

El uso de estas ecuaciones permite que su aplicación tenga un paso angular fijo, donde los puntos se generaran de forma equidistante al centro, es una única expresión para todos los puntos, reduciendo el número de cálculos para el algoritmo.

Simetría de la circunferencia - Alfredo Weitzenfeld (2017)

Para los puntos más alejados del centro, estos pueden ser unidos con segmentos de línea recta, para los puntos más cercanos se puede aplicar el tamaño del paso para θ con la expresión 1/r, aprovechando las simetrías, el segundo cuadrante se genera a partir del primero, y el tercer y cuarto de los dos primeros juntos. (Weitzenfeld , 2017)

Esta segunda propuesta, sigue siendo ineficiente por el grado de complejidad, dadas las operaciones trigonométricas a realizar, es entonces que ahora partiremos a la tercera propuesta de Bresenham, en donde recordemos que en su algoritmo de línea únicamente hace uso de operaciones con números enteros.

Simetría de la circunferencia en 8 cuadrantes - Oscar García(2018)

(García, 2018) Resume, al algoritmo de Bresenham para circunferencias como un algoritmo que analiza el error entre el valor real de la circunferencia y su valor discretizado, donde en cada paso el algoritmo elegirá el próximo pixel que tenga un menor grado de error al valor real, además hace uso de la simetría de una circunferencia dividida en 8 cuadrantes, donde estos se generan recursivamente a partir de la reflexión del primero.

(Weitzenfeld , 2017) Explica y expone esta propuesta de Bresenham con el nombre de “Algoritmo de punto medio para la circunferencia, donde primeramente se define una función de la circunferencia:

$f_{c}ircunferencia(x,y)=x^{2}+y^{2}-r^{2}$

Que trabaja bajo la condición que cualquier punto en la frontera de la circunferencia satisface a la ecuación con una igualación a cero.

$f_{c}ircunferencia(x,y)=0$

Ahora si el punto esta dentro de la circunferencia, la función será negativa.

$f_{d}entro_{(}x,y)=p$

$f_{d}entro_{(}x,y)-f_{c}ircunferencia(x,y)=p-0=p$

En caso contrario, si el punto esta fuera de la circunferencia, entonces p>0. Dado que estas condiciones son aplicables a dos píxeles cercanos, tenemos:

Véase también

• Analizador Diferencial Digital (algoritmo gráfico) es un algoritmo para el trazado de líneas.
• Algoritmo de Xiaolin Wu es un algoritmo para antialiasing de líneas
• Algoritmo del punto medio para circunferencias es un algoritmo para el trazado de cónicas.

Referencias

Bibliografía

• Watt, Alan (2000). «Rasterizing edges». 3D Computer Graphics (3ª edición). p. 184. ISBN 0-201-39855-9. 
• Miguel Ángel Rodríguez-Roselló, Ediciones Anaya Multimedia (1992) "8088-8086/8087 Programación ENSAMBLADOR en entorno MS DOS" (5ª edición). págs: 821-826 ISBN 9788476141281 ISBN10: 84-7614-128-9
• Garcia, O. (2018). Algoritmo de Bresenham para trazar circunferencias. Blogspot. Recuperado 25 de marzo de 2023, de http://garciaoscar10110795.blogspot.com/p/algoritmo-de-bresenham-para-trazar_13.html
• Weitzenfeld, A.(2017). Gráfica. Cannes ITAM. Recuperado 25 de marzo de 2023, de Linea.PDF (itam.mx)
• Pitteway, M. L. V., & Watkinson, D. J. (1980). Bresenham's algorithm with grey scale. Communications of the ACM, 23(11), 625-626.

Gaol, F. L. (2013). Bresenham Algorithm: Implementation and Analysis in Raster Shape. J. Comput., 8(1), 69-78.

Enlaces externos

• Wikilibros alberga un libro o manual sobre implementaciones del algoritmo de Bresenham.
• Medellín, Héctor E. «Recta». Anaya. Archivado desde el original el 12 de abril de 2011. Consultado el 5 de junio de 2011. 
• «Bresenham 2D, 3D hasta 6D». Archivado desde el original el 14 de marzo de 2010. 

• Datos: Q549860
• Multimedia: Bresenham algorithm / Q549860