Teorema de Bell
El teorema de Bell (también conocido como de Bell-Kochen-Specker) o desigualdades de Bell se aplica en mecánica cuántica para cuantificar matemáticamente las implicaciones planteadas teóricamente en la paradoja de Einstein-Podolsky-Rosen y permitir así su demostración experimental. Debe su nombre al científico norirlandés John S. Bell, que la presentó en 1964.
El teorema de Bell es un metateorema que muestra que las predicciones de la mecánica cuántica (MC) no son intuitivas, y afecta a temas filosóficos fundamentales de la física moderna. Es el legado más famoso del físico John S. Bell. El teorema de Bell es un teorema de imposibilidad, que afirma que:
Ninguna teoría física de variables ocultas locales puede reproducir todas las predicciones de la mecánica cuántica.
Dadas sus implicaciones en el plano de la no localidad, supuso la consagración definitiva de la física cuántica frente a otras teorías de variables ocultas y es considerado por la mayoría de físicos del mundo como el descubrimiento más profundo de la historia de la ciencia. [1]
Introducción[editar]
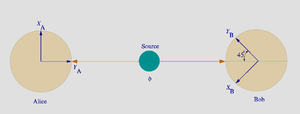
Como en el experimento expuesto en la paradoja EPR, Bell consideró un experimento donde una fuente produce pares de partículas entrelazadas. Por ejemplo, cuando un par de partículas con espines entrelazados es creado; una partícula se envía a Alicia y la otra a Bob. En cada intento, cada observador independientemente elige entre varios ajustes del detector y realiza una medida sobre la partícula (Nota: aunque la propiedad entrelazada utilizada aquí es el espín de la partícula, podría haber sido cualquier "estado cuántico" entrelazado que codifique exactamente un bit cuántico.)
Cuando Alicia y Bob miden el espín de la partícula a lo largo del mismo eje (pero en sentidos opuestos), obtienen resultados idénticos el 100% de las veces.
Pero cuando Bob mide en ángulos ortogonales (perpendiculares) a las medidas de Alicia, obtienen resultados idénticos únicamente el 50% de las veces.
En términos matemáticos, las dos medidas tienen una correlación de 1, o correlación perfecta cuando se miden de la misma forma; pero cuando se miden en ángulos perpendiculares, tienen una correlación de 0; es decir, ninguna correlación. (Una correlación de −1 indicaría tener resultados opuestos en cada medida.)
| Mismo eje: | par 1 | par 2 | par 3 | par 4 | ...n | |
|---|---|---|---|---|---|---|
| Alicia, 0°: | + | − | − | + | ... | |
| Bob, 180°: | + | − | − | + | ... | |
| Correlación: ( | +1 | +1 | +1 | +1 | ...)/n = +1 | |
| (100% idéntica) | ||||||
| Ejes ortogonales: | par 1 | par 2 | par 3 | par 4 | ...n | |
| Alicia, 0°: | + | − | + | − | ... | |
| Bob, 90°: | − | − | + | + | ... | |
| Correlación: ( | −1 | +1 | +1 | −1 | ...)/n = 0.0 | |
| (50% idéntica) |
De hecho, los resultados pueden explicarse añadiendo variables ocultas locales - cada par de partículas podría haberse enviado con instrucciones sobre cómo comportarse según se las mida en los dos ejes (si '+' o '−' para cada eje).
Claramente, si la fuente únicamente envía partículas cuyas instrucciones sean idénticas para cada eje, entonces cuando Alicia y Bob midan sobre el mismo eje, obtendrán siempre resultados idénticos, o bien (+,+) o (−,−). Pero (si se generan por igual todos las posibles combinaciones de + y −) cuando ellos midan sobre ejes perpendiculares verán correlación cero.
Ahora, considere que Alicia o Bob pueden rotar sus aparatos de forma relativa entre ellos un ángulo cualquiera y en cualquier momento antes de medir las partículas, incluso después de que las partículas abandonen la fuente. Si las variables ocultas locales determinan el resultado de las medidas, entonces las partículas deberían codificar en el momento de abandonar la fuente los resultados de medida para cualquier posible dirección de medida, y no solo los resultados para un eje particular.
Bob comienza este experimento con su aparato rotado 45 grados. Llamamos a los ejes de Alicia y , y a los ejes rotados de Bob y . Entonces, Alice y Bob graban las direcciones en que ellos miden las partículas, y los resultados que obtienen. Al final, comparan sus resultados, puntuando +1 por cada vez que obtienen el mismo resultado y −1 si obtienen un resultado opuesto - excepto que si Alicia midió en y Bob midió en , puntuarán +1 por un resultado opuesto y −1 para el mismo resultado.
Utilizando este sistema de puntuación, cualquier posible combinación de variables ocultas produciría una puntuación media esperada de, como máximo, +0.5 (por ejemplo, mirando la tabla inferior, donde los valores más correlacionados de las variables ocultas tienen una correlación media de +0.5, i.e. idénticas al 75%. El "sistema de puntuación" inusual asegura que la máxima correlación media esperada es +0.5 para cualquier posible sistema que esté basado en variables locales).
| Modelo clásico: | variables altamente correlacionadas | variables menos correlacionadas | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variable oculta para 0° (a): | + | + | + | + | − | − | − | − | + | + | + | + | − | − | − | − |
| Variable oculta para 45° (b): | + | + | + | − | − | − | − | + | + | − | − | − | + | + | + | − |
| Variable oculta para 90° (a'): | + | + | − | − | − | − | + | + | − | + | + | − | + | − | − | + |
| Variable oculta para 135° (b'): | + | − | − | − | − | + | + | + | + | + | − | + | − | + | − | − |
| Puntuación de correlación: | ||||||||||||||||
| Si se mide sobre a-b, puntuación: | +1 | +1 | +1 | −1 | +1 | +1 | +1 | -1 | +1 | −1 | −1 | −1 | −1 | −1 | −1 | +1 |
| Si se mide sobre a' − b, puntuación: | +1 | +1 | −1 | +1 | +1 | +1 | −1 | +1 | −1 | −1 | −1 | +1 | +1 | −1 | −1 | −1 |
| Si se mide sobre a'-b', puntuación: | +1 | −1 | +1 | +1 | +1 | −1 | +1 | +1 | -1 | +1 | −1 | −1 | −1 | −1 | +1 | −1 |
| Si se mide sobre a − b', puntuación: | −1 | +1 | +1 | +1 | −1 | +1 | +1 | +1 | −1 | −1 | +1 | −1 | −1 | +1 | −1 | −1 |
| Puntuación esperada promedio: | +0.5 | +0.5 | +0.5 | +0.5 | +0.5 | +0.5 | +0.5 | +0.5 | −0.5 | −0.5 | −0.5 | −0.5 | −0.5 | −0.5 | −0.5 | −0.5 |
El teorema de Bell muestra que si las partículas se comportan como predice la mecánica cuántica, Alicia y Bob pueden puntuar más alto que la predicción clásica de variables ocultas de correlación +0.5; si los aparatos se rotan 45° entre sí, la mecánica cuántica predice que la puntuación esperada promedio será 0.71.
(Predicción cuántica en detalle: cuando las observaciones en un ángulo de se realizan sobre dos partículas entrelazadas, la correlación predicha es . La correlación es igual a la longitud de la proyección del vector de la partícula sobre su vector de medida; por trigonometría, . es 45°, y es , para todos los pares de ejes excepto – donde son 135° y –, pero este último se toma negativo en el sistema de puntuación acordado, por lo que la puntuación total es =0.707. En otras palabras, las partículas se comportan como si cuando Alicia o Bob hacen una medida, la otra partícula decidiese conmutar para tomar esa dirección instantáneamente).
Varios investigadores han realizado experimentos equivalentes utilizando diferentes métodos. Parece que muchos de estos experimentos producen resultados que están de acuerdo con las predicciones de la mecánica cuántica [2], y tienden a refutar las teorías de variables ocultas locales y la demostración de la no localidad. Todavía existen científicos que no están de acuerdo con estos hallazgos [3]. Se encontraron dos escapatorias en el primero de estos experimentos: la de detección y la de comunicación, con los experimentos asociados para cerrar estas escapatorias. Tras toda la experimentación actual parece que estos experimentos dan prima facie soporte para las predicciones de la mecánica cuántica de no localidad [4].
Importancia del teorema[editar]
Este teorema se ha denominado "el más profundo de la ciencia."[1] El influyente artículo de Bell de 1964 se tituló "Sobre la paradoja de Einstein Podolsky Rosen."[2] La paradoja Einstein Podolsky Rosen (paradoja EPR) demuestra, sobre la base de la asunción de "localidad" (los efectos físicos tienen una velocidad de propagación finita) y de "realidad" (los estados físicos existen antes de ser medidos), que los atributos de las partículas tienen valores definidos independientemente del acto de observación. Bell mostró que el realismo local conduce a un requisito para ciertos tipos de fenómenos que no está presente en la mecánica cuántica. Este requisito es denominado desigualdad de Bell.
Después de EPR (Einstein–Podolsky–Rosen), la mecánica cuántica quedó en una posición insatisfactoria:
- o estaba incompleta, en el sentido de que fallaba en tener en cuenta algunos elementos de la realidad física,
- o violaba el principio de propagación finita de los efectos físicos.
En una modificación del experimento mental EPR, dos observadores, ahora comúnmente llamados Alicia y Bob, realizan medidas independientes del espín sobre un par de electrones, preparados en una fuente en un estado especial llamado un estado de espín singlete. Era equivalente a la conclusión de EPR de que una vez Alicia midiese el espín en una dirección ( i.e. sobre el eje x), la medida de Bob en esa dirección estaría determinada con total certeza, con resultado opuesto al de Alicia, mientras que inmediatamente antes de la medida de Alicia, el resultado de Bob estaba solo determinado estadísticamente. Por tanto, o el espín en cada dirección es un elemento de realidad física, o los efectos viajan desde Alicia a Bob de forma instantánea.
En mecánica cuántica (MC), las predicciones se formulan en términos de probabilidades — por ejemplo, la probabilidad de que un electrón sea detectado en una región particular del espacio, o la de que tenga espín arriba o abajo. Sin embargo, persiste la idea de que un electrón tiene una posición y espín definidos, y que la debilidad de la MC es su incapacidad de predecir exactamente esos valores de forma precisa. Queda la posibilidad de que alguna teoría más potente todavía desconocida, como una teoría de variables ocultas, pueda ser capaz de predecir estas cantidades exactamente, y a la vez esté en completo acuerdo con las respuestas probabilísticas dadas por la MC. Si una teoría de variables ocultas fuera correcta, la MC no las describiría, y por lo tanto sería una teoría incompleta.
El deseo de una teoría local realista se basaba en dos hipótesis:
- Los objetos tienen un estado definido, que determina los valores de todas las otras variables medibles, como la posición y el momento.
- Los efectos de las acciones locales, como las mediciones, no pueden viajar más rápido que la velocidad de la luz (como resultado de la relatividad especial). Si los observadores están suficientemente alejados, una medida realizada por uno no tiene efecto en la medida realizada por el otro.
En la formalización del realismo local utilizada por Bell, las predicciones de la teoría resultan de aplicar la probabilidad clásica a un espacio de parámetros subyacente. Mediante un simple (aunque inteligente) argumento basado en la probabilidad clásica, mostró que las correlaciones entre las medidas están acotadas de una forma que es violada por la MC.
El teorema de Bell parece poner punto final a las esperanzas del realismo local para la MC. Por el teorema de Bell, o bien la mecánica cuántica o bien el realismo local están equivocados. Se necesitan experimentos para determinar cuál es correcto, pero llevó muchos años y muchos avances en la tecnología el poder realizarlos.
Los experimentos de prueba de Bell hasta la fecha muestran inequívocamente que las desigualdades de Bell son violadas. Estos resultados proveen evidencia empírica contra el realismo local y en favor de la MC. El teorema de no comunicación prueba que los observadores no pueden utilizar las violaciones de la desigualdad para comunicarse información entre ellos más rápido que la luz.
El artículo de John Bell examina tanto la prueba de 1932 de John von Neumann sobre la incompatibilidad de las variables ocultas con la mecánica cuántica, como el influyente artículo de Albert Einstein y sus colegas de 1935 sobre la materia.
Desigualdades de Bell[editar]
Las desigualdades de Bell se refieren a mediciones realizadas por observadores sobre pares de partículas que han interaccionado y se han separado. De acuerdo con la mecánica cuántica las partículas están en un estado entrelazado, mientras que el realismo local limita la correlación de las siguientes medidas sobre las partículas. Posteriormente, diferentes autores han derivado desigualdades similares a la desigualdad original de Bell, colectivamente denominadas desigualdades de Bell. Todas las desigualdades de Bell describen experimentos donde el resultado predicho asumiendo entrelazamiento difiere del que se deduciría del realismo local. Las desigualdades asumen que cada objeto de nivel cuántico tiene un estado bien definido que da cuenta de todas sus propiedades medibles y que objetos distantes no intercambian información más rápido que la velocidad de la luz. Estos estados bien definidos se llaman a menudo variables ocultas. Son las propiedades que Einstein afirmó cuando hizo su famosa objeción a la mecánica cuántica: "Dios no juega a los dados."
Bell mostró que bajo la mecánica cuántica, que carece de variables locales ocultas, las desigualdades (el límite de correlación) pueden ser violadas. En cambio, las propiedades de una partícula que no son fáciles de verificar en mecánica cuántica pero pueden estar correlacionadas con las de la otra partícula debido al entrelazamiento cuántico, permiten que su estado esté bien definido solo cuando una medida se hace sobre la otra partícula. Esta restricción está de acuerdo con el principio de incertidumbre de Heisenberg, un concepto fundamental e ineludible de la mecánica cuántica.
En el trabajo de Bell:
Los físicos teóricos viven en un mundo clásico, mirando hacia un mundo cuántico. El último es descrito sólo subjetivamente, en términos de procedimientos y resultados sobre nuestro dominio clásico. (...) Nadie conoce dónde se encuentra el límite entre el dominio clásico y el cuántico. (...) Más plausible para mí es que encontremos que no hay límite. Las funciones de onda serían una descripción provisional o incompleta de la parte de la mecánica cuántica. Es esta posibilidad, acerca de una visión homogénea del mundo, lo que constituye para mí la motivación principal que me lleva al estudio de la así llamada posibilidad de las "variables ocultas".(...) Una segunda motivación está conectada con el carácter estadístico de las predicciones de la mecánica cuántica. Una vez se sospecha de la incompletitud de la descripción por funciones de onda, se puede aventurar que las fluctuaciones aleatorias estadísticas están determinadas por las variables adicionales "ocultas" — "ocultas" porque hasta ahora sólo podemos conjeturar su existencia y ciertamente no podemos controlarlas.
(...) Una tercera motivación está en el carácter peculiar de algunas predicciones de la mecánica cuántica, que parecen casi gritar por una interpretación de variables ocultas. Este es el famoso argumento de Einstein, Podolsky y Rosen. (...) Encontramos, sin embargo, que ninguna teoría local determinista de variables ocultas puede reproducir todas las predicciones experimentales de la mecánica cuántica. Esto abre la posibilidad de traer la cuestión al dominio experimental, intentando aproximar tanto como sea posible las situaciones ideales donde las variables locales ocultas y la mecánica cuántica no concuerdan
En teoría de la probabilidad, las mediciones repetidas de las propiedades de un sistema pueden considerarse como muestras repetidas de variables aleatorias. En el experimento de Bell, Alicia puede elegir el ajuste del detector para medir o bien o bien y Bob puede elegir un ajuste del detector para medir o bien o bien . Las medidas de Alicia y Bob deben estar correlacionadas entre sí de alguna forma, pero las desigualdades de Bell dicen que si la correlación proviene de variables aleatorias locales, entonces existe un límite a la magnitud de la correlación que uno puede esperar obtener.
Desigualdad original de Bell[editar]
La desigualdad original que Bell dedujo fue:[2]
donde C es la "correlación" de los pares de partículas y a, b y c ajustes del aparato. Esta desigualdad no se utiliza en la práctica. Por un lado, solo es cierta para sistemas genuinamente de "dos salidas", no para los de "tres salidas" (con posibles salidas de cero además de +1 y −1) encontradas en los experimentos reales. Por otro, se aplica únicamente a un conjunto muy restrictivo de teorías de variables ocultas: solamente a aquellas para las que las salidas a ambos lados del experimento están siempre anticorrelacionadas cuando los analizadores están paralelos, de acuerdo con la predicción de la mecánica cuántica.
Existe un límite simple de la desigualdad de Bell, que tiene la virtud de ser completamente intuitivo. Si el resultado de tres lanzamientos de monedas estadísticamente diferentes A,B,C tienen la propiedad de que:
- A y B son los mismos (ambos caras o ambos cruces) 99% del tiempo,
- B y C son los mismos el 99% del tiempo,
entonces A y C son los mismos por lo menos el 98% del tiempo. El número de discordancias entre A y B (1/100) más el número de discordancias entre B y C (1/100) son el máximo número posible de discordancias entre A y C.
En mecánica cuántica, dejando que A,B,C sean los valores del espín de dos partículas entrelazadas medidas con respecto a algún eje a 0 grados, θ grados, y 2θ grados respectivamente, el solapamiento de la función de onda entre los distintos ángulos es proporcional a . La probabilidad de que A y B den la misma respuesta es , donde es proporcional a θ. Esta es también la probabilidad de que B y C den la misma respuesta. Pero A y C son los mismos 1 − (2ε)2 del tiempo. Eligiendo el ángulo para que , A y B están correlacionados al 99%, B y C están correlacionados al 99% y A y C están correlacionados solo el 96%.
Imagine que dos partículas entrelazadas en un singlete de espín se alejan a dos localizaciones diferentes, y que se miden los espines de ambas en la dirección A. Los espines estarán correlacionados al 100% (realmente, anticorrelacionados pero para este argumento es equivalente). Lo mismo es cierto si ambos espines son medidos en las direcciones B o C. Es seguro concluir que cualquier variable oculta que determinase las medidas de A, B y C en las dos partículas está correlacionada al 100% y puede utilizarse indistintamente en ambas.
Si A se mide en una partícula y B en la otra, la correlación entre ellas es del 99%. Si B ese mide en una y C en la otra, la correlación es del 99%. Esto nos permite concluir que las variables ocultas que determinan A y B están correlacionadas al 99% y las de B y C al 99%. Pero si A se mide en una partícula y C en la otra, los resultados están correlacionados solo en un 96%, lo que es una contradicción. La formulación intuitiva se debe a David Mermin, mientras que el límite del ángulo pequeño se destaca en el artículo original de Bell.
Desigualdad CHSH[editar]
Adicionalmente a la desigualdad de Bell original,[2] la forma dada por John Clauser, Michael Horne, Abner Shimony and R. A. Holt,[3] (the CHSH form) es especialmente importante,[3] porque da límites clásicos a la correlación esperada para el experimiento anterior realizado por Alicia y Bob:
donde C denota correlación.
La correlación de observables X, Y se define como
Esta es una forma no normalizada del coeficiente de correlación considerada en estadística (ver correlación cuántica).
Para formular el teorema de Bell, formalizaremos el realismo local como sigue:
- Existe un espacio de probabilidades y las salidas observadas de Alicia y Bob resultan del muestreo aleatorio del parámetro .
- Los valores observados por Alicia y Bob son funciones de los ajustes del detector local y de los parámetros ocultos únicamente. Luego
- El valor observado por Alicia con el detector ajustado en a es
- El valor observado por Bob con el detector ajustado en b es
Implícita en la asunción 1) de arriba, el espacio de parámetros ocultos tiene una medida de probabilidad y el valor esperado de una variable aleatoria X sobre con respecto a se escribe
donde para mayor legibilidad de la notación asumimos que la medida de probabilidad tiene una densidad.
desigualdad de Bell. La desigualdad CHSH (1) se cumple bajo la asunción de variables ocultas anterior.
Por simplicidad, asumamos primero que los valores observados son +1 or −1; quitaremos esta observación abajo en la Nota 1.
Sea . Entonces por lo menos uno de
es 0. Entonces
y por tanto
Nota 1. La desigualdad de correlación (1) todavía se mantiene si las variables , pueden tomar valor sobre cualquier valor real entre −1 and +1. De hecho, la idea relevante es que cada sumando en la media superior esté acotado superiormente por 2. Es fácil ver que esto es cierto en el caso más general:
Para justificar el límite superior 2 afirmado en la última inecuación, sin pérdida de generalidad, podemos asumir que
En ese caso
Nota 2. Aunque el componente importante del parámetro oculto en la demostración original de Bell está asociado con la fuente y es compartido por Alicia y Bob, puede haber otros que estén asociados con los detectores separados, siendo estos últimos independientes. Este argumento fue utilizado por Bell en 1971, y de nuevo por Clauser y Horne en 1974,[4] para justificar una generalización del teorema forzada sobre ellos por los experimentos reales, donde los detectores nunca tienen una eficiencia del 100%. Las derivaciones fueron dadas en términos de las medias de las salidas sobre las variables locales de los detectores. La formalización del realismo local fue entonces cambiada efectivamente, reemplazando A y B por medias y reteniendo el símbolo pero con uun significado ligeramente diferente. Fue entonces restringido (en muchos trabajos teóricos) a significar solo aquellos componentes que estuvieran asociados con la fuente.
Sin embargo, con la extensión probada en la Nota 1, la desigualdad de CHSH todavía se cumple incluso si los propios instrumentos contienen ellos mismos variables ocultas. En este caso, promediando sobre las variables ocultas del instrumento obtenemos nuevas variables:
sobre que todavía tienen valores en el rango [−1, +1] por lo que podemos aplicar el resultado previo.
Violación de las desigualdades de Bell en la Mecánica Cuántica[editar]
En el formalismo usual de la mecánica cuántica, los observables X e Y son representados como operadores autoadjuntos sobre un espacio de Hilbert. Para computar la correlación, asumimos que X e Y son representados por matrices en un espacio de dimensión finita y que X e Y conmutan; este caso especial es suficiente para nuestros propósitos abajo. El postulado de medida de von Neumann establece que: una serie de medidas de un observable X sobre una serie de sistemas idénticos en el estado produce una distribución de valores reales. Por la asunción de que los observables son matrices finitas, esta distribución es discreta. La probabilidad de observar λ es no nula si y solo si λ es un autovalor de la matriz X y por lo tanto la probabilidad es
donde EX (λ) es el proyector correspondiente al autovalor λ. El estado del sistema inmediatamente tras la medición es
De aquí, podemos mostrar que la correlación de observables que conmutan X e Y en un estado puro es
Apliquemos este hecho en el contexto de la paradoja EPR. Las medidas realizadas por Alicia y Bob son medidas de espín sobre electrones. Alicia puede elegir entre dos ajustes del detector denominados a y a′; estos ajustes corresponden a medidas del espín a lo largo del eje z o del eje x. Bob puede elegir entre dos ajustes del detector denominados b y b′; éstos corresponden a medidas del espín a lo largo del eje z′ o del eje x′, donde el sistema de coordenadas x′ – z′ es rotado 45° relativamente al sistema de coordenadas x – z. Los observables del espín son representados por matrices autoadjuntas 2 × 2 :
Estas son las matrices de espín de Pauli normalizadas para que los correspondientes autovalores sean +1, −1. Como es costumbre, denotamos los autovectores de Sx por
Sea el estado de singlete de espín para un par de electrones como en la paradoja EPR. Este es un estado especialmente construido descrito por los siguientes vectores en el producto tensorial
Ahora apliquemos el formalismo CHSH a las medidas que pueden ser realizadas por Alicia y Bob.

Los operadores , corresponden a las medidas del espín de Bob a lo largo de x′ y z′. Nótese que los operadores A conmutan con los operadores B, por lo que podemos aplicar nuestro cálculo para la correlación. En este caso, podemos mostrar que la desigualdad CHSH falla. De hecho, un cálculo directo muestra que
y
por lo que
Teorema de Bell: Si el formalismo de la mecánica cuántica es correcto, entonces el sistema consistente en un par de electrones entrelazados no puede satisfacer el principio del realismo local. Nótese que es de hecho el límite superior de la mecánica cuántica llamado límite de Tsirelson, que es superior al valor esperado clásicamente: 2. Esto significa que la física cuántica no es local. Los operadores que dan este valor máximo son siempre isomorfos a las matrices de Pauli.
Experimentos prácticos para comprobar el teorema de Bell[editar]
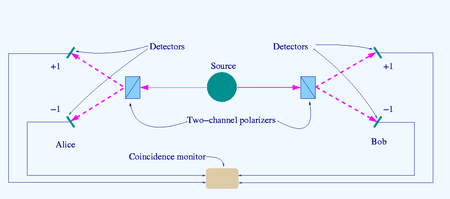
La fuente SOURCE produce pares de "fotones", enviados en direcciones opuestas. Cada fotón encuentra un polarizador de dos canales cuya orientación (a o b) pueda ser ajustada por el experimentador. Las señales emergentes de cada canal son detectadas y las coincidencias de cuatro tipos (++, −−, +− y −+) son contadas por el monitor de coincidencias.
Los tests experimentales pueden determinar si las desigualdades de Bell requeridas por el realismo local se mantienen bajo evidencia empírica.
Las desigualdades de Bell son comprobadas por "contadores de coincidencias" de un experimento de prueba de Bell como el óptico mostrado en el diagrama. Los pares de partículas son emitidos como resultados de un proceso cuántico, analizados con respecto a alguna propiedad clave como la dirección de polarización, y entonces detectados. El ajuste (orientaciones) de los analizadores son seleccionados por el experimentador.
Los resultados experimentales de los test de Bell hasta la fecha violan la desigualdad de Bell de forma flagrante. Además, puede verse una tabla de experimentos de test de Bell realizados antes de 1986 en 4.5 de Redhead, 1987.[5] De los trece experimentos listados, solo dos alcanzaron resultados contradictorios con la mecánica cuántica; además, de acuerdo a la misma fuente, cuando se repitieron los experimentos, "las discrepancias con la MC no pudieron ser reproducidas".
Sin embargo, el asunto no está concluyentemente zanjado. De acuerdo con el artículo divulgativo de Shimony de la enciclopedia de Stanford de 2004:[6]
Muchos de las docenas de experimentos realizados han favorecido a la mecánica cuántica, pero no decisivamente debido a la 'escapatoria de detección' o a la 'escapatoria de comunicación'. La última ha sido decisivamente bloqueada por un experimento reciente y hay buenas perspectivas de poder bloquear también la primera.
Para explorar la 'escapatoria de detección', uno debe distinguir las clases de desigualdades de Bell homogénea e inhomogénea.
La hipótesis estándar en Óptica Cuántica es que "todos los fotones de una frecuencia, dirección y polarización dadas son idénticos" por lo que los fotodetectores tratan todos los fotones incidentes sobre la misma base. Semejante hipótesis de "muestreo justo" generalmente pasa desapercibida, pero limita efectivamente el rango de teorías locales a aquellas que conciben la luz como corpuscular. Esta hipótesis excluye una gran familia de teorías de realismo local, en particular, la descripción de Max Planck. Debemos recordar las palabras cautelosas de Albert Einstein[7] poco antes de morir: "Hoy en día cada Tom, Dick y Harry ('jeder Kerl' en el alemán original) piensa que sabe lo que es un fotón, pero está equivocado".
Las propiedades objetivas del análisis de Bell (teorías realistas locales) incluyen la amplitud de onda de una señal luminosa. Aquellos que mantienen el concepto de dualidad, o simplemente de la luz siendo una onda, reconocen la posibilidad o realidad de que las señales luminosas emitidas tengan un rango de amplitudes y, por lo tanto, que las amplitudes sean modificadas cuando la señal pase a través de dispositivos de análisis como polarizadores o separadores de rayos. Se sigue que no todas las señales tienen la misma probabilidad de detección (Marshall y Santos 2002[5]).
Dos clases de desigualdades de Bell[editar]
El problema del muestreo justo fue encarado abiertamente en la década de 1970. En diseños anteriores de su experimento de 1973, Freedman y Clauser[8] utilizaron muestreo justo en la forma de la hipótesis de Clauser-Horne-Shimony-Holt (CHSH[3]). Sin embargo, poco después Clauser y Horne[4] realizaron la importante distinción entre desigualdades de Bell inhomogéneas (DBI) y homogéneas (DBH). Comprobar una DBI requiere que comparemos ciertas tasas de coincidencia en dos detectores separados con las tasas aisladas de los dos detectores. Nadie necesita realizar el experimento, pues las tasas simples con todos los detectores en la década de 1970 eran como mínimo diez veces todas las tasas de coincidencia. Por ello, teniendo en cuenta esta baja eficiencia del detector, la predicción MC realmente cumplía la DBI. Para llegar al diseño experimental donde la predicción de la MC viola la DBI necesitamos detectores cuya eficiencia exceda del 82% para estados singlete, pero tenemos tasas oscuras muy bajas y tiempos muertos y de resolución muy bajos. Esto está muy por encima del 30% disponible (Brida et al. 2006[6]) por lo que el optimismo de Shimony en la Stanford Encyclopedia, mencionado en la sección precedente, parece exagerado.
Retos prácticos[editar]
Debido a que los detectores no detectan una gran parte de todos los fotones, Clauser y Horne[4] reconocieron que comprobar la desigualdad de Bell requiere algunas asunciones extra. Ellos introdujeron la Hipótesis de no aumento (NEH):
una señal luminosa, originándose por ejemplo en una cascada atómica, tiene una cierta probabilidad de activar un detector. Entonces, si se interpone un polarizador entre la cascada y el detector, la probabilidad de detección no puede aumentar.
Dada esta asunción, hay una desigualdad de Bell entre las tasas de coincidencia con polarizadores y las tasas de coincidencias sin polarizadores.
El experimento fue realizado por Freedman y Clauser,[8] que encontraron que la desigualdad de Bell se violaba. Por lo que la hipótesis de no aumento no puede ser cierta en un modelo de variables ocultas. El experimento de Freedman-Clauser revela que las variables ocultas locales implican el nuevo fenómeno de aumento de la señal:
En el conjunto total de señales de una cascada atómica hay un subconjunto cuya probabilidad de detección aumenta como resultado de pasar a través de un polarizador lineal.
Esto es quizá no sorprendente, puesto que es sabido que añadir ruido a los datos puede, en presencia de un umbral, ayudar a revelar señales ocultas (esta propiedad es conocida como resonancia estocástica [7]). Uno no puede concluir que esta es la única alternativa realista local a la Óptica Cuántica, pero muestra que la escapatoria es sorteada. Además, el análisis conduce a reconocer que los experimentos de la desigualdad de Bell, más que mostrar una ruptura con el realismo o la localidad, son capaces de revelar nuevos fenómenos importantes.
Retos teóricos[editar]
Algunos defensores de la idea de las variables ocultas creen que los experimentos han rechazado las variables ocultas locales. Están preparados para descartar la localidad, explicando la violación de la desigualdad de Bell por medio de una teoría de variables ocultas no local, donde las partículas intercambian información sobre sus estados. Esta es la base de la interpretación de Bohm de la mecánica cuántica, que requiere que todas las partículas en el universo sean capaces de intercambiar información instantáneamente con todas las demás. Un experimento reciente rechazó una gran clase de teorías de variables ocultas "no locales" y no Bohmianas [8]
Si las variables ocultas pueden comunicarse entre sí más rápido que la luz, la desigualdad de Bell puede ser violada con facilidad. Una vez una partícula es medida, puede comunicar las correlaciones necesarias a la otra partícula. Puesto que en relatividad la noción de simultaneidad no es absoluta, esto no es atractivo. Una idea es reemplazar la comunicación instantánea con un proceso que viaje hacia atrás en el tiempo sobre el cono de luz del pasado. Esta es la idea tras la interpretación transaccional de la mecánica cuántica, que interpreta la emergencia estadística de una historia cuántica como una convergencia gradual entre historias que van adelante y atrás en el tiempo.[9]
Un trabajo reciente controvertido de Joy Christian[10] proclama que una teoría determinista, local, y realista puede violar las desigualdades de Bell si los observables son elegidos para ser número no conmutativos en vez de números conmutativos como Bell asumió. Christian proclama que de esta forma las predicciones estadísticas de la mecánica cuántica pueden ser reproducidas exactamente. La controversia sobre este trabajo concierne su proceso de promediado no conmutativo, donde los promedios de los productos de variables en lugares distantes dependen del orden en que aparecen en la integral de promediación. Para muchos, esto parece como correlaciones no locales, aunque Christian define la localidad para que este tipo de cosas estén permitidas.[11][12] En este trabajo, Christian construye una visión de la MC y del experimento de Bell que respeta el entrelazamiento rotacional de la realidad física, que está incluido en la MC por construcción, pues esta propiedad de la realidad se manifiesta claramente en el espín de las partículas, pero no es usualmente tenida en cuenta en el realismo clásico. Tras construir esta vista clásica, Christian sugiere que en esencia, esta es la propiedad de la realidad que origina los valores aumentados de las desigualdades de Bell y como resultado es posible construir una teoría local y realista. Más aún, Christian sugiere un experimento completamente macroscópico, constituido por miles de esferas de metal, para recrear los resultados de los experimentos usuales.
La función de onda de la mecánica cuántica también puede proveer de una descripción realista local, si los valores de la función de onda son interpretados como las cantidades fundamentales que describen la realidad. A esta aproximación se la llama interpretación de las realidades alternativas de la mecánica cuántica. En esta controvertida aproximación, dos observadores distantes se dividen en superposiciones al medir un espín. Las violaciones de las desigualdades de Bell ya no son contraintuitivas, pues no está claro qué copia del observador B verá a qué copia del observador A cuando comparen las medidas. Si la realidad incluye todas las diferentes salidas, la localidad en el espacio físico (no en el espacio de salidas) no es ya restricción sobre cómo los observadores divididos pueden encontrarse.
Esto implica que existe una sutil asunción en el argumento de que el realismo es incompatible con la mecánica cuántica y la localidad. La asunción, en su forma más débil, se llama definición contrafactual. Esta establece que si el resultado de un experimento se observa siempre de forma definida, existe una cantidad que determina cuál hubiera sido la salida aunque no se realice el experimento.
La interpretación de las realidades alternativas (o interpretación de los muchos mundos) no es solo contrafactualmente indefinida, sino factualmente indefinida. Los resultados de todos los experimentos, incluso de los que han sido realizados, no están únicamente determinados.
Observaciones finales[editar]
El fenómeno del entrelazamiento cuántico que está tras la violación de la desigualdad de Bell es solo un elemento de la física cuántica que no puede ser representado por ninguna imagen clásica de la física; otros elementos no clásicos son la complementariedad y el colapso de la función de onda. El problema de la interpretación de la mecánica cuántica es intentar ofrecer una imagen satisfactoria de estos elementos no clásicos de la física cuántica.
El artículo EPR "señala" las propiedades inusuales de los estados entrelazados, i.e. el estado singlete anteriormente mencionado, que es el fundamento de las aplicaciones actuales de la física cuántica, como la criptografía cuántica. Esta extraña no localidad fue originalmente un supuesto argumento de Reductio ad absurdum, porque la interpretación estándar podría fácilmente eliminar la acción a distancia simplemente asignando a cada partícula estados de espín definidos. El teorema de Bell mostró que la predicción de "entrelazamiento" de la mecánica cuántica tenía un grado de no localidad que no podía ser explicado por ninguna teoría local.
En experimentos de Bell bien definidos (ver el párrafo sobre "experimentos de test") uno puede ahora establecer que es falsa o bien la mecánica cuántica o bien las asunciones cuasiclásicas de Einstein: actualmente muchos experimentos de esta clase han sido realizados, y los resultados experimentales soportan la mecánica cuántica, aunque algunos creen que los detectores dan una muestra sesgada de los fotones, por lo que hasta que cada par de fotones generado sea observado habrá escapatorias.
Lo que es poderoso sobre el teorema de Bell es que no viene de ninguna teoría física. Lo que hace al teorema de Bell único y lo ha señalado como uno de los más importantes avances en la ciencia es que descansa únicamente sobre las propiedades más generales de la mecánica cuántica. Ninguna teoría física que asuma una variable determinista dentro de la partícula que determine la salida puede explicar los resultados experimentales, solo asumiendo que esta variable no puede cambiar otras variables lejanas de forma no causal.
Notas[editar]
- ↑ Stapp, 1975
- ↑ a b c J. S. Bell, On the Einstein Podolsky Rosen Paradox, Physics 1, 195 (1964)
- ↑ a b c J. F. Clauser, M. A. Horne, A. Shimony and R. A. Holt, Proposed experiment to test local hidden-variable theories, Physical Review Letters 23, 880–884 (1969)
- ↑ a b c J. F. Clauser and M. A. Horne, Experimental consequences of objective local theories, Physical Review D, 10, 526–35 (1974)
- ↑ M. Redhead, Incompleteness, Nonlocality and Realism, Clarendon Press (1987)
- ↑ Article on Bell's Theorem by Abner Shimony in the Stanford Encyclopedia of Philosophy, (2004).
- ↑ A. Einstein in Correspondance Einstein–Besso, p.265 (Herman, Paris, 1979)
- ↑ a b S. J. Freedman and J. F. Clauser, Experimental test of local hidden-variable theories, Phys. Rev. Lett. 28, 938 (1972)
- ↑ Cramer, John G. "The Transactional Interpretation of Quantum Mechanics", Reviews of Modern Physics 58, 647–688, July 1986
- ↑ J Christian, Disproof of Bell's Theorem by Clifford Algebra Valued Local Variables (2007) http://arxiv.org/abs/quant-ph/0703179
- ↑ J Christian, Disproof of Bell's Theorem: Further Consolidations (2007) http://arxiv.org/abs/0707.1333
- ↑ J Christian, Can Bell's Prescription for Physical Reality Be Considered Complete? (2008) http://arxiv.org/abs/0806.3078
Referencias[editar]
- A. Aspect et al., Experimental Tests of Realistic Local Theories via Bell's Theorem, Phys. Rev. Lett. 47, 460 (1981)
- A. Aspect et al., Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell's Inequalities, Phys. Rev. Lett. 49, 91 (1982).
- A. Aspect et al., Experimental Test of Bell's Inequalities Using Time-Varying Analyzers, Phys. Rev. Lett. 49, 1804 (1982).
- A. Aspect and P. Grangier, About resonant scattering and other hypothetical effects in the Orsay atomic-cascade experiment tests of Bell inequalities: a discusión and some new experimental data, Lettere al Nuovo Cimento 43, 345 (1985)
- J. S. Bell, On the problem of hidden variables in quantum mechanics, Rev. Mod. Phys. 38, 447 (1966)
- J. S. Bell, Introduction to the hidden variable question, Proceedings of the International School of Physics 'Enrico Fermi', Course IL, Foundations of Quantum Mechanics (1971) 171–81
- J. S. Bell, Bertlmann’s socks and the nature of reality, Journal de Physique, Colloque C2, suppl. au número 3, Tome 42 (1981) pp C2 41–61
- J. S. Bell, Speakable and Unspeakable in Quantum Mechanics (Cambridge University Press 1987) [A collection of Bell's papers, including all of the above.]
- J. F. Clauser and A. Shimony, Bell's theorem: experimental tests and implications, Reports on Progress in Physics 41, 1881 (1978)
- J. F. Clauser and M. A. Horne, Phys. Rev. D 10, 526–535 (1974)
- E. S. Fry, T. Walther and S. Li, Proposal for a loophole-free test of the Bell inequalities, Phys. Rev. A 52, 4381 (1995)
- E. S. Fry, and T. Walther, Atom based tests of the Bell Inequalities — the legacy of John Bell continues, pp 103–117 of Quantum [Un]speakables, R.A. Bertlmann and A. Zeilinger (eds.) (Springer, Berlin-Heidelberg-New York, 2002)
- R. B. Griffiths, Consistent Quantum Theory', Cambridge University Press (2002).
- L. Hardy, Nonlocality for 2 particles without inequalities for almost all entangled states. Physical Review Letters 71 (11) 1665–1668 (1993)
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press (2000)
- P. Pearle, Hidden-Variable Example Based upon Data Rejection, Physical Review D 2, 1418–25 (1970)
- A. Peres, Quantum Theory: Concepts and Methods, Kluwer, Dordrecht, 1993.
- P. Pluch, Theory of Quantum Probability, PhD Thesis, University of Klagenfurt, 2006.
- B. C. van Frassen, Quantum Mechanics, Clarendon Press, 1991.
- M.A. Rowe, D. Kielpinski, V. Meyer, C.A. Sackett, W.M. Itano, C. Monroe, and D.J. Wineland, Experimental violation of Bell's inequalities with efficient detection,(Nature, 409, 791–794, 2001).
- S. Sulcs, The Nature of Light and Twentieth Century Experimental Physics, Foundations of Science 8, 365–391 (2003)
- S. Gröblacher et al., An experimental test of non-local realism,(Nature, 446, 871–875, 2007).
Lecturas adicionales[editar]
Las siguientes lecturas están pensadas para el público en general.
- Amir D. Aczel, Entanglement: The greatest mystery in physics (Four Walls Eight Windows, New York, 2001).
- A. Afriat and F. Selleri, The Einstein, Podolsky and Rosen Paradox (Plenum Press, New York and London, 1999)
- J. Baggott, The Meaning of Quantum Theory (Oxford University Press, 1992)
- N. David Mermin, "Is the moon there when nobody looks? Reality and the quantum theory", in Physics Today, April 1985, pp. 38–47.
- Louisa Gilder, The Age of Entanglement: When Quantum Physics Was Reborn (New York: Alfred A. Knopf, 2008)
- Brian Greene, The Fabric of the Cosmos (Vintage, 2004, ISBN 0-375-72720-5)
- Nick Herbert, Quantum Reality: Beyond the New Physics (Anchor, 1987, ISBN 0-385-23569-0)
- D. Wick, The infamous boundary: seven decades of controversy in quantum physics (Birkhauser, Boston 1995)
- R. Anton Wilson, Prometheus Rising (New Falcon Publications, 1997, ISBN 1-56184-056-4)
- Gary Zukav "The Dancing Wu Li Masters" (Perennial Classics, 2001, ISBN 0-06-095968-1)
Enlaces externos[editar]
- Sobre la Paradoja de Einstein Podolsky Rosen John S. Bell, Departamento de Física, Universidad de Wisconsin, (Recibido el 4 de Noviembre de 1964)
- ¿Puede Considerarse Completa la Descripción Mecánico Cuántica de la Realidad Física?. A. Einstein, B. Podolsky y N. Rosen, Instituto de Estudios Avanzados, Princeton, Nueva Jersey (Recibido el 25 de Marzo de 1935)
- ¿Puede Considerarse Completa la Descripción Mecánico Cuántica de la Realidad Física?. N. Bohr, Instituto de Física Teórica, Universidad de Copenhague (Recibido el 13 de Julio de 1935)
- Una explicación del teorema de Bell, basada en el artículo de N. D. Mermin, "Bringing Home the Atomic World: Quantum Mysteries for Anybody," Am. J. of Phys. 49 (10), 940 (October 1981)
- Entrelazamiento cuántico Incluye una explicación simple de la desigualdad de Bell.
- Teorema de Bell en arxiv.org
- Refutación del teorema de Bell mediante un álgebra de Clifford de variables locales Refutación del teorema de Bell
- Una demostración simple de la desigualdad de Bell basada en la teoría elemental de conjuntos.



















![{\displaystyle \ (1)\quad \mathbf {C} [A(a),B(b)]+\mathbf {C} [A(a),B(b')]+\mathbf {C} [A(a'),B(b)]-\mathbf {C} [A(a'),B(b')]\leq 2,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8f873a5ec281b3a088b35f28803edb35e15c7de)






































