Serie de datos

Una serie de datos es un conjunto de valores, numéricos o no numéricos, generalmente ligados a una secuencia temporal. Por ejemplo:

• serie de datos pluviométricos diarios: estos datos son directamente observados en las estaciones pluviométricas o meteorológicas, pueden también ser llamadas series primarias;
• serie de datos pluviométricos mensuales, se trata de una elaboración a partir de los datos primarios observados día a día en las estaciones de medición;
• serie de resultados numéricos obtenidos en un ensayo de laboratorio, en este caso puede no tener una relación secuencial.

En el caso de que esté ligado a una serie temporal, se le denomina serie de tiempo.

A partir de los años 1981, se hace cada vez más frecuente la utilización de redes de sensoreamiento remoto, generando de esta forma una serie temporal de observaciones con un intervalo de tiempo que pueden ser muy pequeños. Por ejemplo, en una red de sensoreamiento remoto de precipitaciones, el barrido de los sensores puede hacerse a cada unos pocos minutos.

Ejemplo de serie de datos primarios

Ejemplo de serie de datos primaria (Precipitaciones diarias en una estación genérica).

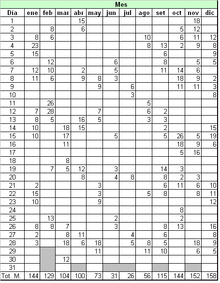
En la figura anexa se presenta un ejemplo de serie de datos primarios, consta de 366 números, y representa la serie de registros de precipitaciones diarias durante todo un año en una estación pluviométrica genérica (en el caso particular, la unidad utilizada es el mm).

Ejemplo de serie de datos secundarios

De la serie anterior, se pueden calcular los totales mensuales, para este caso son:

144; 129; 104; 100; 73; 31; 26; 56; 115; 144; 152; 158

lo que constituye una serie de datos secundarios, que para el ejemplo considerado, son las precipitaciones mensuales en la estación pluviométrica en el año considerado.

Características de una serie de datos numéricos

Las principales características estadísticas de una serie de datos numéricos son:

• Media; en el ejemplo considerado media anual de precipitaciones diarias

$M_{d}=\sum _{i=1}^{365}{\frac {p_{i}}{365}}$

donde:

$M_{d}$ = media diaria anual en mm.

$p_{i}$ = precipitación del día i en mm.

para el caso considerado en el ejemplo sería: $M_{d}={\frac {1323}{365}}=3.38$ mm/día

• Desviación típica "$\sigma$"

$\sigma ={\sqrt {{\frac {1}{365}}\sum _{i=1}^{365}(p_{i}-M_{d})^{2}}}$

• Datos: Q9076310