Rectas que se cruzan

Dos rectas se cruzan si no son paralelas y no se cortan.

Rectas que se cruzan​, en geometría, se denomina a las que no son paralelas ni se intersecan en el espacio. Esto equivale a decir que no pertenecen al mismo plano ya que las rectas coplanares o bien se intersecan o bien son paralelas. Un ejemplo simple de rectas que se cruzan es el par de rectas que recorren los bordes opuestos de un tetraedro regular.

Distancia entre rectas que se cruzan

Distancia entre rectas no coplanares

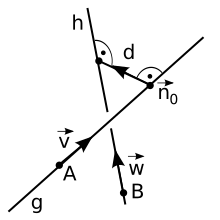
Se define la distancia entre dos rectas que se cruzan como la mínima distancia entre los puntos de una hasta los puntos de la otra. Se sabe que dicho mínimo ocurre cuando ambos puntos están en la perpendicular común a ambas rectas.

Fórmula de la distancia de dos rectas que se cruzan en un espacio afín euclidiano $E\,$:

$d(g,h)=|(a-b)\cdot {\frac {{\vec {v}}\times {\vec {w}}}{|{\vec {v}}\times {\vec {w}}|}}|.$

donde $a+r{\vec {v}}$ y $b+s{\vec {w}}$ son sendas rectas.

Demostración

Dadas las rectas g y h, de ecuaciones paramétricas: $g:{\vec {x}}=a+r{\vec {v}}$ $h:{\vec {x}}=b+s{\vec {w}}\ \ \,r,s\in \mathbb {R}$ donde $r,s\in \mathbb {R}$, ${\vec {v}}$ y ${\vec {w}}$ son vectores directores y $a,b\in E$ Los tres vectores $a-b,{\vec {v}},{\vec {w}}$ son linealmente independientes. El vector normal ${\vec {n}}$ perpendicular a los dos vectores de dirección ${\vec {v}}$ y ${\vec {w}}$ se puede calcular a partir de su producto vectorial: ${\vec {n}}={\vec {v}}\times {\vec {w}}$ y dejarlo de longitud unitaria: ${\vec {n}}_{0}={\frac {{\vec {v}}\times {\vec {w}}}{|{\vec {v}}\times {\vec {w}}|}}$. Entonces, la distancia entre ambas rectas se puede calcular como la proyección de cualquier segmento con extremos en ambas rectas, sobre dicho vector normal. En particular, podemos usar los puntos A y B: $d(g,h)=|(a-b)\cdot {\vec {n}}_{0}|.$

Bibliografía

• Castellet, M.; Llerena, I. (1988). «IV espais vectorials». Àlgebra lineal i geometría (en catalán). Publ. UAB. 
• Real Academia de Ciencias Exactas, Físicas y Naturales, ed. (1999). Diccionario esencial de las ciencias. Espasa. 

Véase también

• Polígono alabeado
• Rectas paralelas

Enlaces externos

• Datos: Q668297
• Multimedia: Skew lines / Q668297