Razonamiento diagramático

El razonamiento diagramático (también llamado razonamiento gráfico o conceptografía) es el que se lleva adelante haciendo uso de representaciones visuales de los conceptos.[2] En esta técnica, los diagramas y los gráficos son más importantes que las palabras y las expresiones matemáticas.[3]
El origen de esta forma de razonamiento debe buscarse en los grafos de Llull y Leibniz, las líneas de Leibniz y los diagramas de Euler.[4] Sin embargo, una expresión equivalente a "razonamiento diagramático" —aunque aplicada específicamente a una notación de dos dimensiones— recién aparece en 1879 con la publicación del libro Begriffsschrift de Gottlob Frege, que ha sido traducido al castellano como Conceptografía.[5] La historia del razonamiento diagramático incluye también la creación por parte de Peirce del sistema de gráficos existenciales, una notación geométrica-topológica-lógica que Gardner consideraba "el más ambicioso sistema de lógica geométrica que se haya construido jamás".[6] [7][8] Shin hizo luego una extensión de esos gráficos hasta convertirlos en una herramienta equivalente a la técnica clásica de operación con predicados monádicos de primer orden.[9] En la tradición de considerar a la lógica como "lenguaje universal" trabajaron Leibniz, Frege, Russell, Wittgenstein, Carnap, Quine, Strawson y, más recientemente, Luetich.[7][10] Se ha mostrado que el lenguaje de diagramas y gráficos permite establecer relaciones de largo alcance: por ejemplo, entre las matemáticas, la ontología, la dialéctica, la lógica, la semiología y la fenomenología.[11][12][13]
Lingua y calculus[editar]

La characteristica universalis es el lenguaje formal universal que Leibniz imaginó para expresar conceptos matemáticos, científicos y filosóficos.[10] En su vasta obra, Leibniz formuló el lenguaje universal de varias maneras, un resumen de las cuales se encuentra en la serie de artículos editados por G. H. R. Parkinson.[14]
El objetivo de Leibniz era usar ese lenguaje en un sistema de cálculo lógico universal de tipo computacional, el calculus ratiocinator.[15] En palabras del propio Leibniz, con un sistema tal, «de surgir controversias, dos filósofos no tendrían que discutir más que dos matemáticos. Sería suficiente que tomaran papel y lápiz, se sentaran y dijeran: ‹¡Calculemos!›».[16] De ahí que Russell haya traducido la expresión latina characteristica universalis como "matemática universal".[16]
En resumen, la propuesta de Leibniz era: encontrar un lenguaje que permita aplicar reglas de inferencia a conceptos matemáticos y no matemáticos.
| razonamiento diagramático | lenguaje | characteristica universalis |
| demostraciones | calculus ratiocinator |
El lenguaje tiene sus reglas de construcción, llamadas reglas sintácticas. Las demostraciones son hechas respetando reglas que establecen la dirección del razonamiento, las reglas semánticas.
Muchos pensadores retomaron esta idea de Leibniz. Frege, por ejemplo, introdujo la Conceptografía como un calculus ratiocinator con su lingua characteristica, y —según Kluge— esa obra estuvo conscientemente inspirada en las ideas de Leibniz.[17] Otros pensadores, en cambio, no la mencionaron. Tal es el caso de Peirce, quien creía que todo razonamiento era, en última instancia, diagramático.[18]
El genio de Leibniz fue reconocido por Grassmann cuando, en la introducción a su Análisis Geométrico, dejó escrito que ideas como la de la characteristica ponían al filósofo por encima de otros pensadores de su tiempo.[19] Sobre este punto volvió mucho después Heath.[20] Norbert Wiener veía en la máquina de Leibniz un antecedente de las computadoras actuales.
Lenguaje[editar]
Los diagramas constituyen el lenguaje de este tipo de razonamiento. También son usados los grafos, que establecen conexiones y en muchos aspectos son equivalentes a los diagramas.
Diagramas[editar]
El sistema universal de Leibniz tenía dos componentes: un lenguaje (characteristica) y un método (calculus). Ambos eran inseparables al punto que sus nombres son usados muchas veces como sinónimos. Este hecho se puede interpretar de dos maneras:
- detrás de ambos está la lógica,[21] lo cual obliga a darle a la voz griega λóγος simultáneamente los significados de "palabra" y "razón",[22] o
- las definiciones son una cosa (ontología) y las operaciones que con ellas se hace son otra (lógica).[23]
Adoptando el segundo punto de vista, los diagramas pueden ser clasificados en ontológicos (los de Euler, los de Venn de conjuntos y los totales), topológicos (los diagramas de Peirce extendidos, los de Shin y los diagramas con arañas) o lógicos (los de Venn de enunciados y los diagramas "alfa" y "beta" de Peirce).
Diagramas ontológicos[editar]
Son los diagramas que muestran entes ("elementos") y las definiciones que a ellos se les ha aplicado ("conjuntos").[24]
Diagramas de Leibniz[editar]
En los primitivos diagramas de Leibniz los conjuntos eran representados con líneas continuas. Las mismas se superponían en las intersecciones (indicadas con segmentos discontinuos).

|
| diagrama de Leibniz |
Leibniz también usó círculos, pero encontró que en ciertos casos estos requerían signos suplementarios. Las líneas de Leibniz constituyen una muestra de la lingua characteristica.[25]
Diagramas de Euler[editar]

En los diagramas de Euler (a veces llamados "círculos de Euler"), se muestran las líneas de definición de los conjuntos y cada región (de elementos propios o de superposición) contiene al menos un elemento.

|
| diagrama de Euler |
Cuando no hay elementos que respondan a cierta combinación de definiciones, la región no se representa.
Los diagramas de Euler hicieron de puente entre los primitivos diagramas de Leibniz y los diagramas de Venn, ampliamente usados hoy.
Diagramas de Venn de conjuntos[editar]

Los diagramas de Venn de conjuntos muestran todas las regiones posibles (en este caso, 7, dos de ellas sombreadas por estar vacías) más la región de los elementos que no responden a ninguna definición (totalizando 8).
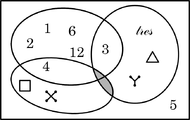
|
| diagrama de Venn de conjuntos |
El rectángulo del diagrama de Venn representa el conjunto de los elementos tomados en cuenta (conjunto universal, U). Venn nunca representó al universal en sus trabajos, pero fue quien introdujo la expresión "universo del discurso".
Diagramas totales 2D[editar]
Los diagramas totales de dos dimensiones muestran los elementos definidos, los que no responden a ninguna definición y algunos de los que no han sido considerados.

|
| diagrama total 2D |
En el diagrama total en dos dimensiones se representa la región de las definiciones, el "cosmos" (blanca), y la de lo no definido, el "caos" (gris); ambas constituyen el Todo.[12] El diagrama total permite resolver de manera elegante el problema que Humpty Dumpy le planteó a Alicia en la obra A través del espejo de Lewis Carroll. Este problema no es tan sencillo como lo hace parecer el formato de cuento infantil elegido por el autor porque plantea a un mismo tiempo el dilema matemático "ser A-ser no A" y la cuestión filosófica "mostrarse-ocultarse".[26]
Diagramas topológicos[editar]
Son los diagramas que muestran la posición relativa de los conjuntos, pero no los elementos. La forma, el tamaño y la posición de las líneas cerradas no tienen importancia.
Regiones posibles[editar]
En los diagramas de conjuntos de Euler y de Venn se pone énfasis en indicar las regiones posibles. En los diagramas de Euler, solamente son representadas las regiones en las que puede haber elementos. En los diagramas de Venn, a las regiones que no contienen elementos se las anula sombreándolas.[27]

|

|
| diagrama de Euler | diagrama de Venn |
En estos ejemplos se muestra que no hay elementos que pertenezcan a A y C que no sean también de B, ni tampoco elementos que pertenezcan exclusivamente a C. En el diagrama de Venn de conjuntos cada región sombreada es —para usar una expresión de Leibniz— una combinatio impossibilis. Se trata entonces de diagramas topológicos.[28]
Topología flexible[editar]
En un intento por flexibilizar la topología de los sistemas, Peirce introdujo en los diagramas de Venn la notación lógica correspondiente a la disyunción. Con ello creó los diagramas de topología flexible. A esta extensión de Peirce siguieron otras dos (Venn-I y Venn-II), propuestas por Shin.[29]
Extensión de Peirce[editar]

La extensión de Peirce de los diagramas de Euler-Venn introduce tres símbolos:
- "o" para reemplazar al sombreado,
- "x" para indicar importación existencial, y
- "–" (línea) para unir los dos anteriores e indicar disyunción.[29]
Así, por ejemplo, el siguiente diagrama representa la proposición: «Todo elemento de B es de A o algunos elementos de B son de A».

|
| extensión de Peirce |
Esta proposición topológica no se podría representar con un diagrama de Euler: sería necesario usar dos y buscar alguna manera de indicar la disyunción.

|

|
| «Todo elemento de B es de A» | «Algunos elementos de B son de A» |
Las ventajas de la notación de Peirce, en este caso, son grandes. Sin embargo, cuando las proposiciones son más complejas, la lectura del diagrama se torna dificultosa.[29]
Primera extensión de Shin (Venn-I)[editar]
Esta extensión tiene las siguientes características:
- vuelve al sombreado de regiones para indicar que éstas no pueden ser ocupadas,
- usa el símbolo "x" de Peirce, y
- usa el símbolo "–", introducido por Peirce.[29]
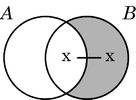
|

|
| diagrama de Shin (Venn-I) | diagrama de Peirce |
En estos diagramas (equivalentes), las dos premisas son:
- «Ningún elemento es sólo de B», y
- «B tiene algún elemento».
La conclusión, por lo tanto, es: «Algún elemento pertenece simultáneamente a B y A».
Segunda extensión de Shin (Venn-II)[editar]
Esta extensión tiene las mismas características que el anterior, pero agrega la posibilidad de conectar dos diagramas —que en este caso tienen representado el conjunto universal— con una línea de disyunción.[29]

|

|
| diagrama de Shin (Venn-II) | diagrama de Peirce |
La proposición, en este caso, es: «O todo elemento de A es elemento de B y algún elemento de A es de B, o ningún elemento de A es de B y algún elemento de B no es de A». El diagrama simple de Peirce es de lectura más difícil que el correspondiente diagrama doble de Shin.
Arañas[editar]
Los diagramas con arañas son una extensión de los diagramas de Euler, y por lo tanto en ellos hay información topológica. Se los obtiene introduciendo restricciones de dos tipos: agregando "arañas" (secuencias x de Peirce generalizadas) y sombreando regiones. La presencia de una araña indica la existencia de un elemento en su "hábitat" (la región donde se encuentra). Una región sombreada es la que no contiene más elementos que los que indican las arañas correspondientes. Si una región sombreada no tiene arañas, está vacía. Dos arañas unidas por una línea indican la existencia de por lo menos un elemento en las regiones involucradas. El nombre "araña" se ha elegido porque en diagramas complejos muchas líneas pueden salir de cada punto, como los hilos de un nodo de una telaraña.[27]

|
| diagrama con arañas |
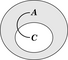
El diagrama de la figura indica que:
- C está contenido en B;
- A – B tiene exactamente dos elementos;
- hay al menos un elemento en B – A.
El diagrama tiene 3 líneas límite de conjuntos (definiciones), indicadas con los rótulos A, B y C, y 6 regiones, por ejemplo la región cuyo contorno es B pero que no contiene elementos ni de A ni de C. Una zonas está sombreada y contiene sólo 2 elementos. El diagrama contiene 3 arañas: 2 de un pie cuyo hábitat es la zona de los elementos de A que no pertenecen a B y 1 "articulada", en la región de los elementos que son de B pero no de A.[27]
Diagramas lógicos[editar]
Son los diagramas que muestran los resultados de operaciones lógicas.
Diagramas de Venn de enunciados[editar]
Los diagramas de Venn de enunciados muestran el resultado de una operación con enunciados (en este caso, A ∨ B) con colores, que en este caso son: verde, cuando la región corresponde al resultado; rojo, cuando no. Éste es el código del semáforo de dos colores.

|
| diagrama de Venn de enunciados |
Gráficos existenciales "alfa" de Peirce[editar]
En los gráficos existenciales "alfa" de Peirce (gráficos que conectan enunciados), la conjunción se representa colocando los enunciados sin solución de continuidad y la negación se representa como un "recorte" de la "hoja de enunciados" (una línea curva cerrada). En el siguiente diagrama se muestra la proposición ¬((¬A) ∧ (¬B)), equivalente a A ∨ B.[6]

|
| gráfico "alfa" de Peirce |
Al hacer demostraciones o cuando los diagramas son complejos, es conveniente sombrear las zonas encerradas por un número impar de recortes, como se ha hecho más abajo.
Gráficos existenciales "beta" de Peirce[editar]
En los gráficos existenciales "beta" de Peirce (gráficos que conectan predicados), hay cuantificadores aplicados a entes, no a definiciones. A estas expresiones Peirce las llamó "de primer orden". En estos gráficos, el autor introdujo la "línea de identidad" o "línea de importación existencial" (–):
- la expresión –A se lee «algo [o alguien] es A», es decir, ∃x | x ∈ A;
- la expresión A—B se lee «algo [o alguien] es A y B», es decir, ∃x | x ∈ A ∧ x ∈ B.
Del mismo modo que en los gráficos "alfa", las conexiones de dos predicados pueden ser hechas recurriendo a "recortes".[18]
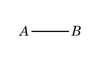
|
«algún A es B» | |

|
«ningún A es B» | |

|
«algún A no es B» | |

|
«todo A es B» |
La notación de la columna izquierda evita que los recortes ocupen tanto espacio.
Diagrama total 3D[editar]
El diagrama total de tres dimensiones es una extensión de los diagramas de Venn que forma parte de la teoría del conocimiento presentada en una serie de artículos filosóficos por Juan José Luetich.[24] Su estructura es la de un árbol con tres bifurcaciones.[30] Las dos primeras surgieron de un análisis de la obra Sobre la Naturaleza de Parménides.[30] La última corresponde a un diagrama de Venn de una sola definición.[31]

|

|
| diagrama total 3D | clave para interpretar las regiones |
De todos los entes que la mente humana puede concebir (reales, imaginarios, concretos, abstractos), el Todo, unos pocos forman parte de su universo, U. De esos entes, a su vez, sólo algunos se corresponden con una definición o concepto, A. Los entes definidos —por responder a una definición o por oponerse a ella (A o ~A)— forman parte de la región blanca, el universo o "cosmos", ya que han sido "ordenados" por la definición. Los entes no definidos existen, pero están ocultos en la región gris, forman parte del "caos", del lugar donde no hay conceptos ni orden.[12]
Grafos[editar]
Los grafos son construcciones que surgen de representar elementos y sus conexiones.[32] La teoría de grafos, como la teoría de conjuntos, está íntimamente ligada a la topología.[33][34]
Cuadrado de oposición[editar]

Aristóteles, al fundar la lógica, puso su atención en algunos cuantificadores usados en el lenguaje natural: todo, algún, ningún, no todo.[35] Estos pueden ser expresados usando la notación de Peirce de predicados (gráficos existenciales "beta"). El clásico "cuadrado de oposición de juicios" de Aristóteles quedaría entonces representado como se muestra en la figura.

|
| El "cuadrado de oposición" de Aristóteles en la notación de Peirce |
Diamante de Leibniz[editar]

En el grabado de la portada del libro De Arte Combinatoria de 1666, Leibniz habría dado otra muestra de su lenguaje universal.[36] En él se representa la idea de los antiguos de que todas las cosas materiales están hechas de tierra, agua, aire y fuego, "elementos" que combinan las cualidades de: frío, húmedo, caliente y seco. Entre elementos, entre cualidades, y entre elementos y cualidades, han sido dibujadas líneas, cada una con un rótulo. Así, por ejemplo, a los nodos SICCITAS y HVMIDITAS ("sequedad" y "humedad") se los ha conectado con una línea rotulada Combinatio impossibilis ("combinación imposible"). En otros términos, de los elementos de estos dos conjuntos, el grabado muestra las conexiones, objeto de estudio de la topología. La characteristica es, en este caso, una notación topológica.[37] El siguiente grafo es una variante del Diamante de Leibniz, que muestra la relación entre elementos y cualidades a la manera de un grafo bipartido.[37]

Cuando dos cualidades concurren en un elemento es porque su combinación es posible. Por ejemplo, CALIDITAS y HVMIDITAS concurren en AER. Cuando dos cualidades no se encuentran en ningún elemento, su combinación es imposible. Tal es el caso de HVMIDITAS y SICCITAS.[37] Con estos elementos y cualidades, sujetas a las restricciones mencionadas, se puede deducir la cantidad de combinaciones posibles.
El diamante de Leibniz puede ser representado sin recurrir a un grafo partido, simplemente usando cuatro conjuntos. En este caso, a menos que a los conjuntos se los dibuje como rectángulos, quedarían regiones vacías. Para indicar esa situación se puede hacer uso de un diagrama con arañas.[37]

|

|
| diagrama de conjuntos | diagrama con arañas |
Estas representaciones actuales del tema que Leibniz tomó de los antiguos para ilustrar su libro de análisis combinatorio muestran lo que ha sido la historia del razonamiento diagramático, un área de trabajo en la que se ha vuelto siempre sobre los mismos complejos problemas, desde la perspectiva de especialistas en las materias más diversas.[37]
Árboles[editar]
Los árboles son unos grafos especiales con estructura jerárquica, que pueden ser usados para dar la misma información topológica que los diagramas de Euler y de Venn.[31][38]

|

|
| árbol del diagrama de Euler | diagrama de Euler |
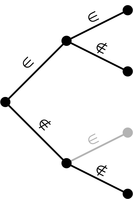
|

|
| árbol del diagrama de Venn | diagrama de Venn |
Cada árbol muestra las regiones posibles del diagrama que está a su derecha. Las primeras 2 ramas corresponden al conjunto A; las restantes 4, al conjunto B. En el diagrama de Euler, la rama de no pertenencia (∉) a A aparece de color gris, ya que no es una región posible. En consecuencia, también están de ese color las ramas derivadas. En el diagrama de Venn, dado que se define un conjunto universal, la no pertenencia a A es posible, exceptuando el caso de pertenencia (∈) simultánea a B.[31]
Notación bidimensional[editar]

La notación bidimensional de Frege permite representar las operaciones lógicas con conexiones.[39]

|
| notación bidimensional de Frege |
Este esquema representa la disyunción lógica A ∨ B, o mejor, ¬A → B.[40]
En su trabajo sobre los axiomas del cálculo proposicional, Frege recurría sólo a las operaciones negación e implicación.
Obsérvese que la notación de los diagramas "beta" de Peirce —con recortes abreviados o no— también es bidimensional, como se puede ver claramente en la lista de reglas de inferencia.
Demostraciones[editar]
Las deducciones sirven son operaciones que se realizan con los diagramas o grafos para obtener resultados o conclusiones.
Reglas de inferencia de Peirce[editar]
Las siguientes reglas permiten obtener nuevas proposiciones —en la forma de diagramas "alfa" o "beta"— a partir de proposiciones dadas.[18]
- Regla de borrado e inserción: Cualquier expresión (enunciado, proposición o parte de línea de identidad) encerrada por un número par de recortes o por ningún recorte puede ser borrada; cualquier expresión puede ser colocada en un área encerrada por un número impar de recortes.
- Borrado en los diagramas "alfa"
A ( B ( C ) ) → ( B ( C ) )
A ∧ ¬(B ∧ ¬C) → ¬(B ∧ ¬C)
La regla de borrado permite reducir una conjunción a uno de sus constituyentes. - Inserción en los diagramas "alfa"
( A ) → ( A B )
¬A → ¬(A ∧ B)
Esta regla está justificada porque una conjunción es falsa con la sola condición de que uno de sus constituyentes sea falso. - Borrado en los diagramas "beta"

«algún A no es B» → «algo [o alguien] es A y algo [o alguien] no es B» → «algo [o alguien] no es B»
Una línea de identidad encerrada por un número par de recortes o por ningún recorte puede ser cortada. - Inserción en los diagramas "beta"

«algo [o alguien] es A y nada [o nadie] es B» → «algún A no es B»
Dos líneas de identidad encerradas por un número impar de recortes pueden ser unidas.
- Borrado en los diagramas "alfa"
- Regla de iteración y desiteración: Cualquier expresión puede ser copiada en el área abarcada por todos los recortes que encierran a la original o en un nivel más profundo, pero no en el interior o exterior de ella misma; cualquier expresión puede ser borrada si puede haber resultado de una iteración.
- Iteración en los diagramas "alfa"
A ( B ) → A ( A B )
A ∧ ¬B → A ∧ ¬(A ∧ B)
Aquí se ha iterado A en un nivel más profundo.
En cambio, sería incorrecto deducir A ( B ( B ) ) o A B ( B ). - Desiteración en los diagramas "alfa"
A ( A B ) → A ( B )
A ∧ ¬(A ∧ B) → A ∧ ¬B
Aquí se ha desiterado A de un nivel más profundo.
En cambio, sería incorrecto deducir A ( B ) de A ( B ( B ) ) o A B ( B ). - Iteración en los diagramas "beta"


Esta deducción parte de la afirmación: «No es el caso que (algún A es B y nada [o nadie] es C)». En la segunda transformación, una línea de identidad se ramifica, lo cual es lícito siempre que el extremo libre ingrese a un círculo, aunque puede apoyarse en él. La iteración también habilita a crear una línea con un extremo libre dentro de dos círculos y a unirla luego a la línea correspondiente de la expresión iterada. Por otra parte, la iteración también permite unir los extremos libres de las partes más internas de dos líneas, como se vio en la regla de inserción. - Desiteración en los diagramas "beta"
La desiteración permite revertir todas las transformaciones mencionadas en el punto anterior.
- Iteración en los diagramas "alfa"
- Regla de aserción: Cualquier expresión verdadera puede ser representada en la hoja sin líneas que la encierren.
Esta regla permite introducir premisas. Las premisas deben ser representadas una al lado de la otra y constituyen una conjunción. - Regla de doble recorte: Alrededor de cualquier expresión se puede insertar un par de círculos; dos círculos que rodean a una expresión pueden ser eliminados. No debe haber nada entre los círculos.
- Regla de deformación: Cualquier expresión puede ser deformada siempre que las conexiones no sean alteradas.
Esta regla muestra el carácter topológico de la notación de Peirce.
Ejemplos de aplicación de estas reglas son: para los diagramas "alfa", la demostración del "Teorema Brillante" de Leibniz; para los diagramas "beta", la deducción silogística.
Sistema de demostraciones de Shin[editar]
El razonamiento humano es heterogéneo, en el sentido de que involucra palabras y símbolos, pero también imágenes, diagramas y modelos. Por otra parte, para procesar esa información, el ser humano usa relaciones semánticas entre proposiciones ("similitud intuitiva") y procedimientos no deductivos (como la "abducción"). Desde áreas de trabajo diversas, han sido hechas distintas aproximaciones al "razonamiento multimodal".[41]
En cuanto a la comparación del razonamiento simbólico con el razonamiento diagramático, se ha mostrado que no hay diferencia entre ambos en lo que a "estatus lógico" se refiere. En 1994, Shin presentó los diagramas Venn-I y Venn-II como un sistema de representación formal con su propia sintaxis y semántica. Las reglas sintácticas indican si un diagrama es aceptable, en el sentido de si está bien formado y qué transformaciones están permitidas. La semántica se ocupa de las consecuencias lógicas. Así se comprueba que los sistemas mencionados son robustos y completos, en el mismo sentido que lo son algunos sistemas lógicos simbólicos.[9] Este resultado da por tierra con la arraigada creencia de que los sistemas de diagramas pueden llevar a deducciones erróneas y que por lo tanto hay que abstenerse de usarlos en demostraciones.[9][42][29]
Aplicaciones[editar]
El razonamiento diagramático ha encontrado aplicación en diversas áreas de trabajo: máquinas de calcular, algoritmos de demostración de proposiciones, semiótica, ciencias de la cognición, inteligencia artificial (IA), teoría del conocimiento, filosofía del lenguaje, ontología.[24][13][3]
Machina ratiocinatrix[editar]

(Staffelwalze)
Con el calculus ratiocinator, Leibniz tenía un objetivo más ambicioso que el de Pascal, ya que él no tenía en mente un dispositivo mecánico para hacer cálculos aritméticos sino una machina ratiocinatrix.[43][44] El calculus ratiocinator era un algoritmo que, aplicado a una expresión simbólica escrita con la characteristica universalis, determinaría si dicha fórmula es o no verdadera.[45] Sin embargo Leibniz —con los medios disponibles en su tiempo— sólo logró construir la máquina de calcular llamada Staffelwalze ("cilindro dentado", por la forma del dispositivo mecánico de cálculo que utiliza), conocida hoy como "Máquina de Leibniz". La computadora digital es para muchos la materialización de la machina ratiocinatrix.[46]
Demostración del "Teorema Brillante"[editar]
La siguiente es la demostración del resultado que Leibniz llamó Praeclarum Theorema ("Teorema Brillante"): «Si A implica C y B implica D, entonces A y B implican C y D».[47] En símbolos, la tesis es la siguiente.
(A ⊃ C) ∧ (B ⊃ D)) ⊃ ((A ∧ B) ⊃ (C ∧ D))
La demostración se puede hacer aplicando las reglas indicadas más arriba para los diagramas "alfa" de Peirce. Para facilitar la lectura y el uso de las reglas 1 y 2, las regiones rodeadas por un número impar de recortes aparecen de color gris; las regiones rodeadas por un número par de recortes o por ningún recorte están en blanco.[47]

Aquí se ha aplicado primero la regla de doble recorte (4) a la hoja de enunciados en blanco. Luego han sido insertadas dos expresiones en la región gris (regla 1). Luego han sido aplicadas sucesivamente las reglas de: iteración (2), inserción (1), iteración (2) y desiteración (2). Por último, eliminando un doble recorte (regla 4), se llegó al diagrama correspondiente a la tesis del teorema.
Deducción silogística[editar]
La siguiente deducción se hace aplicando las reglas correspondientes a los diagramas "beta" de Peirce.[18]
- Dos premisas son introducidas usando la regla de aserción (3): «Todo A es B» y «todo B es C».

- Se hace la iteración de la segunda premisa usando la regla 2.

- Se borra la segunda premisa usando la regla 1.

- Se aplica la regla de iteración (2).
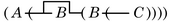
- Se aplica la regla de inserción (1).

- Se aplica la regla de desiteración (2).
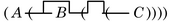
- Se aplica la regla de deformación (5).

- Se aplica la regla de doble recorte (4).
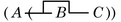
- Se aplica la regla de borrado (1).

- Se aplica la regla de deformación (5).

La conclusión es entonces: «Todo A es C».
Usando la notación de recortes completos, la misma deducción quedaría representada como sigue.
 1 (premisas) | |||
 2 |
 3 |
 4 |
 5 |
 6 |
 7 |
 8 |
 9 |
 10 (conclusión) | |||
Animaciones del pensamiento[editar]
Las deducciones de los dos puntos anteriores son una serie de figuras que, mostradas una a continuación de otra, constituyen animaciones. Dau las llama "animaciones del pensamiento".[48] En efecto, son una representación abstracta de los procesos mentales que conducen a una conclusión. Si bien la interpretación de estas animaciones requiere el conocimiento de las convenciones de Peirce, también es cierto que un ser inteligente podría descubrir las reglas a partir de la observación de varias secuencias.
Interfaces gráficas de usuario[editar]
Nakatsu mostró cómo el uso de diagramas ha facilitado el diseño de sistemas de inteligencia artificial del tipo interfaz de usuario para tareas de toma de decisión y resolución de problemas.[49] En estas interfaces los diagramas facilitan la interacción de los operadores con las cada vez más complejas tecnologías de la información. En particular, permiten comprender y visualizar sistemas de IA. Con el razonamiento diagramático es posible programar usando técnicas que emulan el pensamiento humano y la capacidad de resolución de problemas. Entre estas técnicas, cabe mencionar:
- los "sistemas expertos",
- el "razonamiento basado en modelos",
- el "razonamiento inexacto" (los "factores de certeza" y las "redes bayesianas"), y
- el "razonamiento lógico",
que han encontrado aplicaciones en las ciencias físicas, la medicina, la macroeconomía, las finanzas y la logística.
Véase también[editar]
Referencias[editar]
- ↑ "Camino del ser y diagrama total" Archivado el 18 de febrero de 2014 en Wayback Machine., Actas – Editoriales, Rosario, Academia Luventicus, 2013
- ↑ Gerard Allwein y Jon Barwise (editores), Logical Reasoning with Diagrams, Studies in Logic and Computation, Nueva York, Oxford University Press, 1996
- ↑ a b Michael Anderson, "Reasoning with Diagrammatic Representations", AI Magazine, Vol. 19 No. 2, Palo Alto, Association for the Advancement of Artificial Intelligence, 1998
- ↑ Margaret E. Baron, "A Note on the Historical Development of Logic Diagrams: Leibniz, Euler and Venn", The Mathematical Gazette, Vol. 53 No. 384, Leicester, The Mathematical Association, 1969
- ↑ Friedrich Ludwig Gottlob Frege, Begriffsschrift. Eine Der Arithmetischen Nachgebildete Formelsprache Des Reinen Denkens, Halle, Louis Nebert, 1879
- ↑ a b Charles Hartshorne – Paul Weiss (compiladores), capítulo IV: "Symbolic Logic" – "Existential Graphs" – "On Existential Graphs, Euler’s Diagrams, and Logical Algebra", The Collected Papers of Charles Sanders Peirce, Cambridge, Harvard University Press, 1931–5
- ↑ a b João Queiroz – Frederik Stjernfelt, "Introduction: Diagrammatical reasoning and Peircean logic representations", Semiotica, Vol. 186 No. 1/4, Berlín, Walter de Gruyter, 2011
- ↑ Martin Gardner, Logic machines and diagrams, Chicago, University of Chicago Press, 1982
- ↑ a b c Sun-Joo Shin, The logical status of diagrams, Cambridge, Cambridge University Press, 1994
- ↑ a b "Diagramas ontológicos: de Leibniz a Luetich" Archivado el 16 de enero de 2014 en Wayback Machine., Actas – Editoriales, Rosario, Academia Luventicus, 2013
- ↑ Juan José Luetich, "Ontología y dialéctica", Actas – Suplemento 1, 1 (1) 2, Rosario, Academia Luventicus, 2003
- ↑ a b c Juan José Luetich, "Glosario de ontología", Actas – Suplemento 1, 1 (2) 1, Rosario, Academia Luventicus, 2003
- ↑ a b Frederik Stjernfelt, The Diagrammatology: An investigation on the borderlines of phenomenology, ontology, and semiotics, Dordrecht, Springer Verlag, 2007
- ↑ G. H. R. Parkinson, Leibniz: Logical Papers, Oxford, Clarendon, 1966
- ↑ Nicholas Rescher, "Review of On the Project of a Universal Character by Jonathan Cohen", Journal of Symbolic Logic, Vol. 19 No. 133, Newton, Association for Symbolic Logic, 1969
- ↑ a b Bertrand Russell, A critical exposition of the philosophy of Leibniz, with an appendix of leading passages, Cambridge, Cambridge University Press, 1900
- ↑ E. H. W. Kluge, "Frege, Leibniz and the notion of an ideal language", Studia Leibnitiana, 12, Stuttgart, Franz Steiner, 1980.
- ↑ a b c d P. N. Johnson-Laird, "Peirce, logic diagrams, and the elementary operations of reasoning", Thinking and reasoning, Vol. 8 No. 1, Abingdon, Psychology Press, 2002
- ↑ Hermann Günther Grassmann, Geometrische Analyse geknüpft an die von Leibniz erfundene geometrische Charakteristik, Leipzig, Weidmann'sche Buchhandlung, 1847
- ↑ A. E. Heath, "The geometrical analysis of Grassmann and its connection with Leibniz's characteristic", The Monist, Vol. 27 No. 1, Búfalo, Hegeler Institute, 1917
- ↑ Jean van Heijenoort, "Logic as calculus and logic as language", Synthese, 17, Dordrecht, Springer, 1967
- ↑ Juan José Luetich, "Ser y pertenecer", Actas – Suplemento 1, 1 (2) 1, Rosario, Academia Luventicus, 2008
- ↑ Juan José Luetich, "Logos: inteligencia, palabra, sentido, razón", Actas – Suplemento 1, 1 (6) 1, Rosario, Academia Luventicus, 2004
- ↑ a b c Volumen I: "Filosofía y Humanidades" Archivado el 25 de marzo de 2014 en Wayback Machine. Actas – Suplemento 1, Rosario, Academia Luventicus
- ↑ L. Couturat (editor), "Generales Inquisitiones de Analysi Notionum et Veritatum", Opuscules et Fragments Inédits de Leibniz, París, Alcan, 1903
- ↑ "El no cumpleaños de Humpty Dumpty" Archivado el 9 de enero de 2014 en Wayback Machine., Actas – Editoriales, Rosario, Academia Luventicus, 2013
- ↑ a b c John Howse – Gem Stapleton – John Taylor, "Spider diagrams", Journal of Computation and Mathematics, 8, Londres, London Mathematical Society, 2005
- ↑ Juan José Luetich, "Operaciones con tres onjuntos" Archivado el 23 de octubre de 2013 en Wayback Machine., Luventicus – Universidad, 15, Rosario, Academia Luventicus, 2003
- ↑ a b c d e f Edward N. Zalta – Uri Nodelman – Colin Allen (editores), artículo: "Diagrams", Stanford Encyclopedia of Philosophy, Stanford, Metaphysics Research Lab – Center for the Study of Language and Information – Stanford University, 2001–2013
- ↑ a b Juan José Luetich, "Las tres bifuraciones del Camino del Ser", Actas – Suplemento 1, 1 (2) 3, Rosario, Academia Luventicus, 2003
- ↑ a b c "Diagramas y árboles" Archivado el 14 de marzo de 2014 en Wayback Machine., Actas – Editoriales, Rosario, Academia Luventicus, 2013
- ↑ W. T. Tutte, Graph Theory, Cambridge, Cambridge University Press, 2001
- ↑ J. L. Gross – T. W. Tucker, Topological graph theory, Nueva York, Wiley Interscience, 1987
- ↑ Kenneth Kunnen – Jerry E. Vaughan (editores), Handbook of Set-Theoretic Topology, Ámsterdam, North Holland, 1985
- ↑ Duilio D'Alfonso, "Generalized Quantifiers: Logic and Language"], Logic and Philosophy of Science, Vol. 9 No. 1, Trieste, Dipartimento di Studi Umanistici – Università degli Studi di Trieste, 2011
- ↑ Gottfried Wilhelm Leibniz, Dissertatio de Arte Combinatoria, 1666
- ↑ a b c d e "El Diamante de Leibniz" Archivado el 19 de febrero de 2014 en Wayback Machine., Actas – Editoriales, Rosario, Academia Luventicus, 2013
- ↑ Reinhard Diestel, Graph Theory, 3a. edición, Berlín – Nueva York, Springer, 2005
- ↑ Dov M. Gabbay – John Woods, The Rise of Modern Logic: From Leibniz to Frege, Handbook of the History of Logic, Vol. 3, Ámsterdam, Elsevier – North Holland, 2004
- ↑ Edward N. Zalta – Uri Nodelman – Colin Allen (editores), artículo: "Gottlob Frege", Stanford Encyclopedia of Philosophy, Stanford, Metaphysics Research Lab – Center for the Study of Language and Information – Stanford University, 2001–2013
- ↑ Selmer Bringsjord – Yingrui Yang, "Human reasoning is heterogeneous—as Jon Barwise informed us", Journal of Experimental & Theoretical Artificial Intelligence, Taylor & Francis, 2006.
- ↑ E. Hammer, “Reasoning with Sentences and Diagrams”, Notre Dame Journal of Formal Logic, Vol. 35 No. 1, 1995
- ↑ Norbert Wiener, "The Human Use of Human Beings", Cybernetics and Society, Vol. 20, Boston, Houghton Mifflin, 1950
- ↑ Norbert Wiener, Cybernetics, Second Edition: or the Control and Communication in the Animal and the Machine, Boston, MIT Press, 1965
- ↑ Hartley Rogers Jr., "An Example in Mathematical Logic", The American Mathematical Monthly, Vol. 70 No. 9, Washington, The Mathematical Association of America, 1963
- ↑ Norbert Wiener, "Time, communication, and the nervous system", "Teleological mechanisms", Annals of the New York Academy of Sciences, Vol. 50 No. 4, Nueva York, John Wiley, 1948
- ↑ a b Charles Sanders Peirce, Existential Graphs with commentary by John F. Sowa, MS514, 1909
- ↑ Frithjof Dau, Leibniz' splendid theorem as moving-picture of Thought, 2014
- ↑ Robbie Nakatsu, Diagrammatic Reasoning in AI, Nueva York, John Wiley & Sons, 2010
Enlaces externos[editar]
- Suplemento de la revista Actas de la Academia Luventicus dedicado a la difusión de la obra de Juan José Luetich (ISSN 1666-7581).
- Página oficial de la revista Studia Leibnitiana en el sitio de la editorial Franz Steiner.
- Tesis doctoral "Diagramas lógicos de Marlo para el razonamiento visual y heterogéneo: válidos en lógica matemática y aristotélica".
