Portal:Matemática/Artículo portada/Archivo
 Artículos de Interés en el Portal[editar]
Artículos de Interés en el Portal[editar]
- π (pi)
- Topología
- Teoría de grafos
- ábaco
- Último Teorema de Fermat
- cuadrado mágico
- Teoría de Juegos
- Dilema del prisionero
- cubo de Rubik
Para nominar artículos a Artículos de Interés del Portal Matemática colocarlos aquí:
- (vacio)
- (vacio)

π (pi) es una constante matemática cuyo valor es igual a la proporción existente entre el perímetro de la circunferencia y la longitud de su diámetro, se emplea frecuentemente en matemática, física e ingeniería. El valor numérico de π truncado a sus diez primeras posiciones decimales, es el siguiente:
La notación con la letra griega π proviene de la inicial de las palabras de origen griego "περιφέρεια" (periferia) y "περίμετρον" (perímetro) de una circunferencia. Fue conocida anteriormente como constante de Ludoph (en honor al matemático Ludolph van Ceulen) o como constante de Arquímedes (No confundir con número de Arquímedes). El valor computado de esta constante ha sido conocido con diferentes precisiones a lo largo de la historia, de esta forma en una de las referencias documentadas más antiguas como la Biblia (Reyes 1 7:23) aparece de forma indirecta asociada con el número natural 3 y en Mesopotamia los matemáticos la empleaban como 3 y una fracción añadida de 1/8. π es una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e.
|
La Topología es una disciplina Matemática que estudia las propiedades de los espacios topológicos y las funciones continuas. La Topología se interesa por conceptos como proximidad, número de agujeros, el tipo de consistencia (o textura) que presenta un objeto, comparar objetos y clasificar, entre otros múltiples atributos donde destacan conectividad, compacidad, metricidad, etcétera.
Generalmente se presenta la Topología como la "Geometría de la página de goma". Esto hace referencia a que en la Geometría euclídea dos objetos serán equivalentes mientras podamos transformar uno en otro mediante isometrías , es decir, mediante transformaciones que conservan las medidas de ángulo, longitud, área, volumen y otras. En Topología, dos objetos son equivalentes en un sentido mucho más amplio. Han de tener el mismo número de trozos, de agujeros, de intersecciones, etc. En topología está permitido doblar, estirar, encoger, retorcer, etc., los objetos pero siempre que se haga sin romper ni separar lo que estaba unido, ni pegar lo que estaba separado. Por ejemplo, un triángulo es topológicamente lo mismo que una circunferencia, ya que podemos transformar uno en otra de forma continua, sin romper ni pegar. Pero una circunferencia no es lo mismo que un segmento (ya que habría que partirla por algún punto).

|

En Matemáticas y ciencias de la computación, la Teoría de grafos estudia las propiedades de los grafos, que son colecciones de objetos llamados vértices (o nodos) conectados por líneas llamadas aristas (o arcos) que pueden tener orientación (dirección asignada).
El trabajo de Leonhard Euler, en 1736, sobre el problema de los puentes de Königsberg es considerado como uno de los primeros resultados de la teoría de grafos. También se considera uno de los primeros resultados topológicos en geometría (que no depende de ninguna medida).
|

Una calculadora es una máquina utilizada para realizar cálculos aritméticos. Aunque las calculadoras modernas incorporan a menudo un ordenador de propósito general, se diseñan para realizar ciertas operaciones más que para ser flexibles. Por ejemplo, existen calculadoras gráficas especializadas en campos matemáticos gráficos como la trigonometría y la estadística. También suelen ser más portátiles que la mayoría de computadores, si bien algunas PDAs tienen tamaños similares a los modelos típicos de calculadora.
En el pasado, se utilizaban como apoyo al trabajo numérico ábacos, comptómetros, ábacos neperianos, tablas matemáticas, reglas de cálculo y máquinas de sumar. El término «calculador» se usaba para aludir a la persona que ejercía este trabajo, ayudándose también de papel y lápiz.
|
La aleatoriedad es un campo de definición que, en matemáticas, se asocia a todo proceso cuyo resultado no es previsible más que en razón de la intervención del azar. El resultado de todo suceso aleatorio no puede determinarse en ningún caso antes de que este se produzca. Por consiguiente, los procesos aleatorios quedan englobados dentro del área del cálculo de probabilidad y, en un marco más amplio en el de la estadística.
La palabra aleatorio se usa para expresar una aparente carencia de propósito, causa, u orden. El término aleatoriedad se usa a menudo como sinónimo con un número de propiedades estadísticas medibles, tales como la carencia de tendencias o correlación.
La aleatoriedad ocupa un lugar importante en la ciencia y la filosofía.
|


Un cuadrado mágico es la disposición de una serie de números enteros en un cuadrado de forma tal que la suma de los números por columnas, filas y diagonales sea la misma, llamada la constante mágica.
En la antigua China ya se conocían los cuadrados mágicos desde el III milenio a. C., como atestigua el Lo Shu. Según la leyenda, un cierto día se produjo el desbordamiento de un río; la gente, temerosa, intentó hacer una ofrenda al dios del río Lo (uno de los desbordados) para calmar su ira. Sin embargo, cada vez que lo hacían, aparecía una tortuga que rondaba la ofrenda sin aceptarla, hasta que un niño se dio cuenta de las peculiares marcas del caparazón de la tortuga, de este modo pudieron incluir en su ofrenda la cantidad pedida (15), quedando el dios satisfecho y volviendo las aguas a su cauce.
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
|

En matemáticas la expresión, 1 − 2 + 3 − 4 + · · · es una serie infinita cuyos términos son los números enteros positivos, que van alternando sus signos. Utilizando notación matemática para sumatorias, la suma de los primeros m términos de la serie se expresa como:
Es una serie divergente, en el sentido que la sucesión de sus sumas parciales (1, −1, 2, −2, …) no tiende a ningún límite finito. En forma equivalente se dice que 1 − 2 + 3 − 4 + · · · no posee suma.
Sin embargo, a mediados del siglo XVIII, Leonhard Euler descubre la siguiente relación calificándola de paradójica:
No será hasta mucho tiempo después que se logra dar con una explicación rigurosa de dicha relación. Hacia comienzos de la década de 1890, Ernesto Cesàro y Émile Borel entre otros, investigaron métodos bien definidos para encontrar sumas generalizadas de las series divergentes – incluyendo nuevas interpretaciones de los intentos realizados por Euler. Muchos de estos métodos denominados de sumación le asignan a (1 − 2 + 3 − 4 + · · ·) una "suma" de 1⁄4.
|

El Dilema del prisionero es un ejemplo claro pero atípico de un problema de suma no nula. En este problema de teoría de juegos, se supone que cada jugador, de modo independiente, trata de maximizar su propia ventaja sin importarle el resultado del otro jugador. Las técnicas de análisis de la teoría de juegos estándar, por ejemplo determinar el equilibrio de Nash, pueden llevar a cada jugador a escoger traicionar al otro, pero curiosamente ambos jugadores obtendrían un resultado mejor si colaborasen. Desafortunadamente (para los prisioneros), cada jugador está incentivado individualmente para defraudar al otro, incluso tras prometerle colaborar. Éste es el punto clave del dilema.La enunciación clásica del dilema del prisionero es:
- La policía arresta a dos sospechosos. No hay pruebas suficientes para condenarlos, y tras haberlos separado, los visita a cada uno y les ofrece el mismo trato: "Si confiesas y tu cómplice continúa sin hablar, él será condenado a la pena total, 10 años, y tú serás liberado. Si él confiesa y tú callas, tú recibirás esa pena y será él el que salga libre. Si ambos permanecen callados, todo lo que podremos hacer será encerrarlos 6 meses por un cargo menor. Si ambos confiesan, ambos serán condenados a 6 años.
|

Se denomina cuadratura del círculo al problema matemático, irresoluble de geometría, consistente en hallar —con sólo regla y compás— un cuadrado que posea un área que sea igual a la de un círculo dado.
La resolución de este problema trató de abordarse repetidas veces, sin éxito, desde la antigüedad clásica hasta el siglo XIX. Hablando en sentido figurado, se dice de algo que es la "cuadratura del círculo" cuando representa un problema muy difícil o imposible de resolver.
En 1882, el matemático alemán Ferdinand Lindemann publicó un trabajo que probaba que π es un número trascendental, de lo cual podía extraerse la conclusión —alcanzada por métodos no geométricos— de que es imposible cuadrar el círculo sólo con la regla no metrada y el compás. Esto es, el problema es irresoluble.
4 de octubre[editar]
 |
| Construcción de un pentágono regular |
La construcción con regla y compás es el trazado de puntos, segmentos de recta y ángulos usando exclusivamente una regla y compás idealizados. La geometría clásica griega impuso esa norma para las construcciones, aunque los griegos también investigaron las que pueden obtenerse con instrumentos menos básicos.
Los problemas más famosos que se propusieron para su resolución con regla y compás son la cuadratura del círculo, la duplicación del cubo y la trisección del ángulo, a los que a veces se añade la construcción del heptágono regular, el primero de los infinitos polígonos regulares imposibles de crear con regla y compás. Tienen en común ser de resolución imposible: está matemáticamente demostrado que no se puede cuadrar el círculo, ni duplicar el cubo, ni trisecar el ángulo, ni trazar un heptágono regular usando exclusivamente la regla y el compás idealizados de la geometría griega.
4 de octubre[editar]
 |
| Dado, en un juego de azar. |
La aleatoriedad es un campo de definición que, en matemáticas, se asocia a todo proceso cuyo resultado no es previsible más que en razón de la intervención del azar. El resultado de todo suceso aleatorio no puede determinarse en ningún caso antes de que este se produzca. Por consiguiente, los procesos aleatorios quedan englobados dentro del área del cálculo de probabilidad y, en un marco más amplio en el de la estadística.
La teoría matemática de la probabilidad surgió de intentar formular descripciones matemáticas de los eventos de oportunidad, originalmente en el contexto de juegos. Pronto se vieron las posibles conexiones con situaciones de interés en la física. La estadística se usa para inferir la distribución de probabilidad subyacente de una colección de observaciones empíricas. Para los propósitos de la simulación es necesario tener un suministro amplio de números aleatorios, o medidas para generarlos bajo demanda.
24 de octubre[editar]
 |
| Henri Poincaré |
Jules Henri Poincaré (1854–1912), generalmente conocido como Henri Poincaré, fue un prestigioso matemático, científico teórico y filósofo de la ciencia. Poincaré es descrito a menudo como el último «universalista» (luego de Gauss) capaz de entender y contribuir en todos los ámbitos de la disciplina matemática.
En el campo de la mecánica elaboró diversos trabajos sobre las teorías de la luz y las ondas electromagnéticas, y desarrolló, junto a Albert Einstein y H. Lorentz, la Teoría de la Relatividad restringida. La conjetura de Poincaré es uno de los problemas recientemente resueltos más desafiantes de la topología algebraica, y fue el primero en considerar la posibilidad de caos en un sistema determinista, en su trabajo sobre órbitas planetarias.
Las numerosas contribuciones estuvieron relacionadas con los siguientes temas: Topología algebraica, Teoría de funciones analíticas de varias variables complejas, Teoría de funciones abelianas, Geometría algebraica, Teoría de números, El problema de los tres cuerpos, Teoría de ecuaciones diofánticas, Teoría del electromagnetismo. Además realizó aportes en matemática aplicada, tales como Mecánica celeste, Mecánica de fluidos, Óptica, Electricidad, telegrafía, capilaridad, elasticidad, termodinámica, teoría potencial, mecánica cuántica, Teoría de la Relatividad y cosmología.
Productos notables[editar]
 |
| Binomio al cuadrado |
Existen ciertas fórmulas que permiten multiplicar ciertos polinomios de forma directa (sin realizar la multiplicación completa). Tales fórmulas se denominan productos notables.
Los productos notables están relacionados con las fórmulas de factorización estudiadas en los primeros cursos de álgebra, ya que cada producto notable corresponde a una fórmula de factorización. Por ejemplo, el producto de binomios conjugados corresponde a la regla de factorización de diferencia de cuadrados.
Entre los productos notables podemos encontrar el Cuadrado de Binomio, Binomio al Cubo, Diferencia de Cuadrados, Suma de Cubos, etc.
21 de Abril: Potencia de un punto[editar]
 |
| Potencia del punto P |
Si P esta por dentro de a es p al cubo es un punto fijo, y C una circunferencia, la potencia del punto P respecto a C es el producto de sus distancias a cualquier par de puntos de la circunferencia alineados con P. El valor de la potencia es constante para cada punto P, independientemente de la elección de los puntos de la circunferencia.
De manera más formal, si P es un punto, y una recta que pasa por P corta a la circunferencia en A y B, la potencia de P se define como el producto PA × PB, como se muestra en la figura.
Teorema del coseno[editar]
 |
| Notación más habitual de un triángulo. |
El teorema del coseno es una generalización del teorema de Pitágoras en los triángulos no rectángulos que relaciona un lado de un triángulo con los otros dos y con el coseno del ángulo formado por estos dos lados. Es un teorema comúnmente utilizado en trigonometría, y establece que:
Dado un triángulo ABC, siendo α, β, γ, los ángulos, y a, b, c, los lados respectivamente opuestos a estos ángulos entonces:
En la mayoría de los idiomas, este teorema es conocido con el nombre de teorema del coseno, denominación no obstante relativamente tardía. En francés, sin embargo, lleva el nombre del matemático persa Ghiyath al-Kashi que unificó los resultados de sus predecesores.
matemática Inca[editar]
 |
| Representación de un quipu, instrumento de contabilidad y mnemotécnico inca. |
Matemática inca: En el campo de la matemática los incas destacaron principalmente por su capacidad de cálculo en el ámbito económico. Los quipus y yupanas fueron señal de la importancia que tuvo la matemática en la administración incaica. Esto dotó a los incas de una aritmética sencilla pero efectiva, para fines contables, basada en el sistema decimal; desconocieron el cero, pero dominaron la suma, la resta, la multiplicación y la división.
Pequeño teorema de Fermat[editar]
 |
| Pierre de Fermat. |
El pequeño teorema de Fermat es uno de los teoremas clásicos de teoría de números relacionado con la divisibilidad. Se formula de la siguiente manera:
Esto quiere decir que, si se eleva un número a a la p-ésima potencia y al resultado se le resta a, lo que queda es divisible por p (véase aritmética modular). Su interés principal está en su aplicación al problema de la primalidad y en criptografía.
Este teorema no tiene nada que ver con el legendario último teorema de Fermat, que fue sólo una conjetura durante 350 años y finalmente fue demostrado por Andrew Wiles en 1995.
Número primo[editar]
 |
| 12 no es primo, pero 11 si lo es. |
Un Número primo es un número natural que tiene únicamente dos divisores naturales distintos: él mismo y el 1. Euclides demostró alrededor del año 300 a. C. que existen infinitos números primos. Se contraponen así a los números compuestos, que son aquellos que tienen algún divisor natural aparte de él mismo y del 1. El número 1, por convenio, no se considera ni primo ni compuesto.
Los números primos menores que cien son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 y 97. Una forma simple de obtenerlos es por medio de la criba de Eratóstenes.
El estudio de los números primos es una parte importante de la teoría de números, ya que se consideran los «ladrillos» con los que se construye cualquier número natural. Los números primos están presentes en algunas conjeturas centenarias tales como la hipótesis de Riemann y la conjetura de Goldbach.
Una de las aplicaciones más destacadas de los números primos es su uso en el cifrado de datos (criptografía), muy utilizado en Informática.
Problema de los puentes de Königsberg[editar]
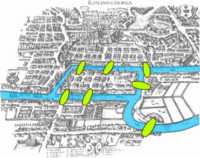 |
| Mapa de Königsberg en la época de Leonhard Euler, que muestra dónde se encontraban los siete puentes (en verde claro) y las ramas del río (en celeste). |
El problema de los puentes de Königsberg, también llamado más específicamente problema de los siete puentes de Königsberg, es un célebre problema matemático, resuelto por Leonhard Euler en 1736 y cuya resolución dio origen a la teoría de grafos. Su nombre se debe a Königsberg, el antiguo nombre que recibía la ciudad rusa de Kaliningrado, que durante el siglo XVIII formaba parte de Prusia Oriental, como uno de los ducados del Reino de Prusia.
Divisores binómicos[editar]
| Forma más común de divisores binómicos. |
Divisores binómicos es un método avanzado de factorización que se usa mayormente en los temas de fracciones algebraicas para este tema es indispensable saber la regla de Ruffini. Su proceso consiste en los siguientes pasos.
Posibles ceros
En este primer paso, los posibles ceros resultan del cociente de la división de los divisores del término independiente entre los divisores del coeficiente principal y se dividen uno por uno.
Nota: Para un mejor entendimiento, este método se explicara con el siguiente ejemplo.
Si el enunciado es este:
Se ve que el término independiente es 6 y el coeficiente principal es 1. Para sacar los posibles ceros se procede de la siguiente manera:
Donde se puede notar que como se menciono anteriormente cada divisor de arriba fue divido por el de abajo; es decir....






