Interferómetro Fabry-Pérot

Cerquillos de interferencia que muestran la estructura fina de un interferómetro de Fabry-Pérot. La fuente de luz es una lámpara fría de deuterio.

En óptica, un interferómetro de Fabry-Pérot, o Etalon está, normalmente, constituido por una placa con dos superficies reflectantes, o dos espejos paralelos altamente reflectantes (técnicamente, el primero es un etalon y el posterior es un interferómetro, pero la terminología se usa, con frecuencia, de manera indistinta). Cuando se determina su espectro de transmisión en función de la longitud de onda se verifica que existen picos de gran transmisión que corresponden a la resonancia del etalon. Se nombró en reconocimiento a Charles Fabry y Alfred Perot.​ "Etalon" proviene del francés étalon, que significa "cálculo de medida" o "estándar".​

El efecto de resonancia de un interferómetro de Fabry-Pérot es idéntico al que se usa en un filtro dicroico. Los filtros dicroicos son colecciones secuenciales muy delgadas de interferómetros de Fabry-Pérot y están así caracterizados y diseñados usando las mismas reglas matemáticas.

Los etalones se usan con bastante frecuencia en telecomunicaciones, láseres y espectroscopia de control y medida de longitudes de onda. Los recientes avances en las técnicas de fabricación han permitido la creación de interferómetros de Fabry-Pérot extremadamente precisos.

Aplicaciones

• La aplicación común más importante es su uso como filtro dicroico, en el que una serie de capa de etalones se depositan sobre una superficie óptica mediante técnicas de deposición de vapor. Estos filtros ópticos tienen, usualmente, una capacidad reflectante exacta y pasan más bandas que los filtros de absorción. Por el propio diseño del filtro funcionan más fríos que los filtros de absorción puesto que pueden reflejar longitudes de onda no deseadas. Los filtros dicroicos se usan ampliamente en equipos ópticos tales como fuentes de luz, cámaras y equipos astronómicos.

• Empleo en redes de telecomunicaciones para el multiplexado de longitudes de onda en equipos add-drop multiplexers con bancos de etalones sintonizados de diamante o sílice fundida. Estos bancos son pequeños cubos iridiscentes de aproximadamente 2 mm de tamaño en un lado, montados en pequeños estantes mecanizados con alta precisión. Los materiales se eligen para mantener estables las distancias espejo a espejo y guardar la estabilidad de las frecuencias usadas en las transmisiones, incluso cuando varia la temperatura. Se prefiere el diamante porque presenta una mejor conducción del calor y un menor coeficiente de dilatación. Desde el año 2005, algunos equipos de comunicaciones comenzaron a usar etalones de estado sólido que son de fibra óptica. Esto elimina la mayoría de las dificultades de montaje, alineamiento y enfriamiento de los equipos.

Análisis Físico

La variación en la función de transmisión es debida a sucesivas reflexiones de la luz entre las superficies. Cuando los dos haces están en fase se da interferencia constructiva, mientras que si están fuera de fase se dará interferencia destructiva. El hecho que dos haces se encuentren o no en fase, depende de la longitud de onda de la luz, $\lambda$; del ángulo con el que la luz atraviesa el etalon, $\theta$; el grosor del etalon, $l$ y el índice de refracción del material, $n$.

La diferencia de fases entre un par de haces transmitidos está dada por δ:​

$\delta =({\frac {2\pi }{\lambda }})2nl\cos \theta$

Si ambas superficies tienen una reflectividad R, la función de Coeficiente de transmisión del etalon está dado por

$T_{e}={\frac {(1-R)^{2}}{1+R^{2}-2R\cos \delta }}={\frac {1}{1+F\sin ^{2}(\delta /2)}},$

donde

$F={\frac {4R}{(1-R)^{2}}}$

es el coeficiente de finesse.

La transmisión de un etalon como función de la longitud de Onda. Un etalon de alta finesse (línea roja) muestra picos más agudos y mínimos de transmisión más pequeños que uno de bajo finesse (en azul).

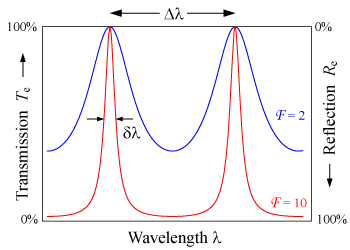
El máximo de transmisión ($T_{e}=1$) ocurre cuando la diferencia entre caminos ópticos ($2nl\cos \theta$) entre los haces transmitidos es un múltiplo de la longitud de onda. En ausencia de absorción la reflectividad del etalon R_e es complemento de la transmitividade tal que $T_{e}+R_{e}=1$. El máximo de reflectividad está dado por:

$R_{\max }=1-{\frac {1}{1+F}}={\frac {4R}{(1+R)^{2}}}$

y estos se da cuando la diferencia de camino es la mitad de un múltiplo impar de la longitud de onda.

Véase también

• Interferometría
• LOFAR

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre Interferómetro Fabry-Pérot.
• Wikcionario tiene definiciones y otra información sobre interferómetro.

• Datos: Q1359945
• Multimedia: Fabry-Pérot interferometer / Q1359945