Guía de onda

En el ámbito del electromagnetismo y en telecomunicación, una guía de ondas es cualquier estructura física que guía ondas electromagnéticas o sonido, con una pérdida mínima de energía al restringir la transmisión de energía en una dirección. Sin la restricción física de una guía de ondas, las intensidades de onda disminuyen de acuerdo con la ley del cuadrado inverso a medida que se expanden en un espacio tridimensional.
Existen diferentes tipos de guías de ondas para diferentes tipos de ondas. El significado original y más común[1] es un tubo metálico conductor hueco que se usa para transportar ondas de radio de alta frecuencia, particularmente microondas. Estas guías se basan en la anulación del campo eléctrico en el conductor. Sin embargo existen guías de ondas basadas en otros principios, como la refracción en dieléctricos. Las guías de ondas dieléctricas se utilizan a frecuencias de radio más altas, y las guías de ondas dieléctricas transparentes y las fibras ópticas sirven como guías de ondas para la luz. En acústica, los conductos de aire y las bocinas se utilizan como guías de ondas para el sonido en instrumentos musicales y altavoces, y varillas de metal de forma especial conducen ondas ultrasónicas en el mecanizado ultrasónico.
La geometría de una guía de ondas refleja su función; además de los tipos más comunes que canalizan la onda en una dimensión, existen guías de ondas de placa bidimensional que limitan las ondas a dos dimensiones. La frecuencia de la onda transmitida también dicta el tamaño de una guía de ondas: cada guía de ondas tiene una longitud de onda de corte determinada por su tamaño y no conducirá ondas de mayor longitud de onda; una fibra óptica que guía la luz no transmitirá microondas que tienen una longitud de onda mucho mayor. Algunas estructuras naturales también pueden actuar como guías de ondas. La capa del canal SOFAR en el océano puede guiar el sonido del canto de las ballenas a través de enormes distancias.[2] Cualquier forma de sección transversal de la guía de ondas puede soportar ondas EM. Las formas irregulares son difíciles de analizar. Las guías de ondas de uso común son de forma rectangular y circular.
Principio de funcionamiento[editar]

Las ondas se propagan en todas direcciones en el espacio abierto como ondas esféricas. La potencia de la onda cae con la distancia R desde la fuente como el cuadrado de la distancia (ley del cuadrado inverso). Una guía de ondas confina la onda para que se propague en una dimensión, de modo que, en condiciones ideales, la onda no pierde potencia mientras se propaga. Debido a la reflexión total en las paredes, las ondas se limitan al interior de una guía de ondas.
Historia[editar]
La primera guía de onda fue propuesta por Joseph John Thomson en 1893 quien sugirió propagar ondas electromagnéticas dentro de una cavidad metálica cilíndrica. Experimentalmente, este hecho fue verificado por el físico británico Oliver Lodge en 1894. El análisis matemático de los modos de propagación de un cilindro metálico hueco fue realizado por primera vez por el también físico británico Lord Rayleigh en 1897.[3] Para ondas sonoras Lord Rayleigh publicó un análisis matemático completo de los modos de propagación en su obra fundamental, "La teoría del sonido".[4] Jagadish Chandra Bose investigó longitudes de onda milimétricas utilizando guías de onda, y en 1897 describió a la Royal Institution de Londres su investigación llevada a cabo en Calcuta.[5]
El estudio de las guías de ondas dieléctricas (como las fibras ópticas, ver más abajo) comenzó ya en la década de 1920 por varias personas, las más famosas de las cuales son Rayleigh, Sommerfeld y Debye.[6] La fibra óptica comenzó a recibir una atención especial en la década de 1960 debido a su importancia para la industria de las comunicaciones.
El desarrollo de la comunicación por radio se produjo inicialmente en las frecuencias más bajas porque estas podían propagarse más fácilmente a grandes distancias. Las longitudes de onda largas hicieron que estas frecuencias no fueran adecuadas para su uso en guías de ondas metálicas huecas debido a los tubos de diámetro impracticablemente grandes requeridos. En consecuencia, la investigación sobre guías de ondas de metal hueco se estancó y el trabajo de Lord Rayleigh fue olvidado por un tiempo y tuvo que ser redescubierto por otros. Investigaciones prácticas reanudadas en la década de 1930 por George C. Southworth en Bell Labs y Wilmer L. Barrow en el MIT. Southworth al principio tomó la teoría de artículos sobre ondas en varillas dieléctricas porque desconocía el trabajo de Lord Rayleigh. Esto lo engañó un poco; algunos de sus experimentos fallaron porque no era consciente del fenómeno de la frecuencia de corte de la guía de ondas que ya se encontraba en el trabajo de Lord Rayleigh. John R. Carson y Sallie P. Mead retomaron un trabajo teórico serio. Este trabajo condujo al descubrimiento de que para el modo TE 01 en la guía de ondas circular las pérdidas disminuyen con la frecuencia y en un momento esto fue un serio competidor para el formato de telecomunicaciones de larga distancia.[7]
La importancia del radar en la Segunda Guerra Mundial dio un gran impulso a la investigación de guías de ondas, al menos en el lado aliado. El magnetrón, desarrollado en 1940 por John Randall y Harry Boot en la Universidad de Birmingham en el Reino Unido, proporcionó una buena fuente de energía e hizo factibles los radares de microondas. El centro de investigación más importante de los EE. UU. estaba en el Laboratorio de Radiación (Rad Lab) del MIT, pero muchos otros participaron en los EE. UU. y en el Reino Unido, como el Establecimiento de Investigación de Telecomunicaciones. El jefe del Grupo de Desarrollo Fundamental en Rad Lab fue Edward Mills Purcell. Sus investigadores incluyeron a Julian Schwinger, Nathan Marcuvitz, Carol Gray Montgomery y Robert H. Dicke. Gran parte del trabajo de Rad Lab se concentró en encontrar modelos de elementos agrupados de estructuras de guías de ondas para que los componentes de las guías de ondas pudieran analizarse con la teoría de circuitos estándar. Hans Bethe también estuvo brevemente en Rad Lab, pero mientras estuvo allí produjo su teoría de la pequeña apertura que resultó importante para los filtros de cavidad de guía de ondas, desarrollada por primera vez en Rad Lab. La parte alemana, por otro lado, ignoró en gran medida el potencial de las guías de ondas en el radar hasta muy tarde en la guerra. Tanto es así que cuando se enviaron piezas de radar de un avión británico derribado a Siemens & Halske para el análisis, aunque fueron reconocidos como componentes de microondas, no se pudo identificar su propósito.
- "En ese momento, las técnicas de microondas estaban muy desatendidas en Alemania. En general, se creía que no era de utilidad para la guerra electrónica, y aquellos que querían realizar trabajos de investigación en este campo no estaban autorizados a hacerlo."
- H. Mayer, vicepresidente en tiempo de guerra de Siemens & Halske
Incluso se permitió a los académicos alemanes continuar publicando sus investigaciones en este campo porque no se consideraba importante. [9]
Inmediatamente después de la Segunda Guerra Mundial, la guía de ondas fue la tecnología elegida en el campo de las microondas. Sin embargo, tiene algunos problemas; es voluminoso, caro de producir y el efecto de la frecuencia de corte dificulta la producción de dispositivos de banda ancha. La guía de ondas estriada puede aumentar el ancho de banda más allá de una octava, pero una mejor solución es utilizar una tecnología que funcione en modo TEM (es decir, sin guía de ondas) como los conductores coaxiales, ya que TEM no tiene una frecuencia de corte. También se puede utilizar un conductor rectangular blindado, que tiene ciertas ventajas de fabricación sobre el cable coaxial y puede considerarse el precursor de las tecnologías planas (stripline y microstrip). Sin embargo, las tecnologías planas realmente comenzaron a despegar cuando se introdujeron los circuitos impresos. Estos métodos son significativamente más baratos que la guía de ondas y han ocupado su lugar en la mayoría de las bandas. Sin embargo, la guía de ondas todavía se ve favorecida en las bandas de microondas más altas desde alrededor de la banda Ku hacia arriba. [10]
Introducción[editar]
Algunos sistemas de telecomunicaciones utilizan la propagación de ondas electromagnéticas en el espacio libre, sin embargo también se puede transmitir información mediante el confinamiento de estas ondas en cables o guías. En SHF, banda de frecuencia donde se encuentran las microondas, las líneas de transmisión y los cables coaxiales presentan atenuaciones muy elevadas por lo que introducen mucha pérdida al voltaje y corriente de superalta frecuencia que viaja por ellos, impidiendo que la microonda llegue a su destino con un nivel de potencia apropiado para que la información que transporta pueda ser extraída sin errores.
Mientras que en las líneas de transmisión (coaxiales por ejemplo) lo que viaja por ellos es un voltaje y una corriente de alta o muy alta frecuencia, por las guías de onda lo que viaja es un campo electromagnético cuya longitud de onda se encuentra en el orden de las microondas.
La transmisión de señales por guías de onda reduce la disipación de energía, es por ello que se utilizan en las frecuencias denominadas de microondas con el mismo propósito que las líneas de transmisión en frecuencias más bajas, ya que se presentan poca atenuación para el manejo de señales de alta frecuencia.
Este nombre, se utiliza para designar los tubos de un material de sección rectangular, circular o elíptica, en los cuales la energía electromagnética ha de ser conducida principalmente a lo largo de la guía y limitada en sus fronteras. Las paredes conductoras del tubo confinan la onda al interior por reflexión, debido a la ley de Snell en la superficie, donde el tubo puede estar vacío o relleno con un dieléctrico. El dieléctrico le da soporte mecánico al tubo (las paredes pueden ser delgadas), pero reduce la velocidad de propagación.
En las guías, los campos eléctricos y los campos magnéticos están confinados en el espacio que se encuentra en su interior, de este modo no hay pérdidas de potencia por radiación y las pérdidas en el dieléctrico son muy bajas debido a que suele ser aire. Este sistema evita que existan interferencias en el campo por otros objetos, al contrario de lo que ocurría en los sistemas de transmisión abiertos.
Principios de operación[editar]
Dependiendo de la frecuencia, se pueden construir con materiales conductores o dieléctricos. Generalmente, cuanto más baja es la frecuencia, mayor es la guía de onda. Por ejemplo, el espacio entre la superficie terrestre y la ionosfera, la atmósfera, actúa como una guía de onda. Las dimensiones limitadas de la Tierra provocan que esta guía de onda actúe como cavidad resonante para las ondas electromagnéticas en la banda ELF. (véase Resonancia Schumann).
Las guías de onda también pueden tener dimensiones de pocos centímetros. Un ejemplo puede ser aquellas utilizadas por los satélites de EHF, por los radares y por los aceleradores lineales de electrones.
Análisis[editar]
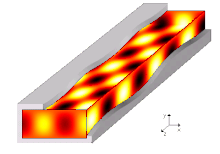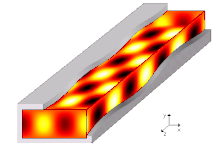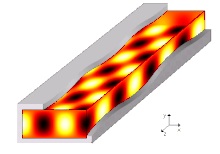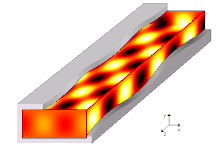
Las guías de onda electromagnéticas se analizan resolviendo las ecuaciones de Maxwell con las condiciones de borde que impone la guía. Estas ecuaciones tienen soluciones múltiples, o modos, que son los autofunciones del sistema de ecuaciones. Cada modo es pues caracterizado por un autovalor, que corresponde a la velocidad de propagación axial de la onda en la guía.
Los modos de propagación dependen de la longitud de onda, de la polarización y de las dimensiones de la guía. El modo longitudinal de una guía de onda es un tipo particular de onda estacionaria formado por ondas confinadas en la cavidad. Los modos transversales se clasifican en tipos distintos:
- Modo TE (Transversal eléctrico), la componente del campo eléctrico en la dirección de propagación es nula.
- Modo TM (Transversal magnético), la componente del campo magnético en la dirección de propagación es nula.
- Modo TEM (Transversal electromagnético), la componente tanto del campo eléctrico como del magnético en la dirección de propagación es nula.
- Modo híbrido, son los que sí tienen componente en la dirección de propagación tanto en el campo eléctrico como en el magnético.
En guías de onda rectangulares el modo fundamental es el TE1,0 y en guías de onda circulares es el TE1,1.
El ancho de banda de una guía de onda viene limitado por la aparición de modos superiores. En una guía rectangular, sería el TE0,1. Para aumentar dicho ancho de banda se utilizan otros tipos de guía, como la llamada "Double Ridge", con sección en forma de "H".
Desarrollo matemático[editar]
Supongamos que una guía rectilínea está tendida en la dirección , y que transporta una onda monocromática (es decir, de frecuencia angular constante ), entonces los campos eléctricos y magnético que se propagan en el interior de la guía a lo largo de dicha dirección, serán expresados de la siguiente forma:
donde las coordenadas y son constantes. Si en el interior de la guía no hay cargas ni corrientes libres, las ecuaciones de Maxwell que relacionan a un campo respecto al otro, tomarán la forma:
donde el símbolo representa al operador nabla.
La ecuación de ondas, aplicando la definición de los campos (el campo magnético tendría una forma análoga), queda expresada así:
Definiendo:
se tiene que las ecuaciones toman la forma de la ecuación de Helmholtz:
Descomponiendo los campos en componentes longitudinales ( y ) y transversales ( y ):
se puede separar de la ecuación de Helmholtz la componente longitudinal, obteniendo:
La función o que cumple unas ciertas condiciones de contorno impuestas por el tipo de guía, se denomina potencial de Debye.
Modos TE y TM[editar]
Se tratará el caso de un modo TE, para el caso del modo TM tan solo hay que intercambiar en las expresiones el campo eléctrico y magnético. En un modo TE se tiene que:
También se tiene que:
de modo que:
El campo B longitudinal será la solución de la ecuación de Helmholtz y el campo transversal puede obtenerse a partir de la anterior expresión. El campo eléctrico vendrá dado por las ecuaciones de Maxwell. Dependiendo de la naturaleza de la guía, o (cuyo desarrollo sería idéntico) han de cumplir unas ciertas condiciones de contorno.
Guía conductora[editar]
El sistema consiste en una región que se extiende simétricamente a lo largo del eje limitada por un material conductor de espesor despreciable (un ejemplo de esto sería un cilindro hueco cuyos radios interior y exterior son prácticamente iguales). Si el espesor del conductor es lo suficientemente pequeño y dado que la condición de confinamiento impone que los campos en el exterior sean nulos, por las ecuaciones de Maxwell se tiene que:
siendo un vector unitario normal (perpendicular) a la superficie de la guía. La continuidad del campo eléctrico implicaría que no existen pérdidas por efecto Joule en el interior del conductor pero dado que tales condiciones son aproximaciones (dado que el espesor del conductor nunca será nulo), si existe una corriente superficial que produce tales pérdidas. Al margen de lo anterior, la corriente producida es lo suficientemente pequeña como para no invalidar el desarrollo empleado.
Usos[editar]

Las guías de onda son muy adecuadas para transmitir señales debido a sus bajas pérdidas. Por ello, se usan en microondas, a pesar de su ancho de banda limitado y volumen, mayor que el de líneas impresas o coaxiales para la misma frecuencia. También son usadas en la construcción de dispositivos en guías de onda, como acopladores direccionales, filtros, circuladores y otros.
Actualmente, son especialmente importantes, y lo serán más en el futuro, las guías de onda dieléctricas que trabajan a frecuencias de la luz visible e infrarroja, habitualmente llamadas fibra óptica, útiles para transportar información de banda ancha, las cuales sustituyen a los cables coaxiales y enlaces de microondas en las redes telefónicas y, en general, las redes de datos.
Los usos de las guías de ondas para transmitir señales se conocían incluso antes de que se acuñara el término. El fenómeno de las ondas sonoras guiadas a través de un cable tenso se conoce desde hace mucho tiempo, así como el sonido a través de una tubería hueca como una cueva o un estetoscopio médico. Otros usos de las guías de ondas son la transmisión de potencia entre los componentes de un sistema, como radio, radar o dispositivos ópticos. Las guías de ondas son el principio fundamental de las pruebas de ondas guiadas (GWT), uno de los muchos métodos de evaluación no destructiva.
Ejemplos específicos:
- Las fibras ópticas transmiten luz y señales a largas distancias con baja atenuación y una amplia gama utilizable de longitudes de onda.
- En un horno de microondas, una guía de ondas transfiere energía desde el magnetrón, donde se forman las ondas, a la cámara de cocción.
- En un radar, una guía de ondas transfiere energía de radiofrecuencia hacia y desde la antena, donde la impedancia debe coincidir para una transmisión de energía eficiente (ver más abajo).
- Las guías de onda rectangulares y circulares se utilizan comúnmente para conectar alimentaciones de platos parabólicos a su electrónica, ya sea receptores de bajo ruido o amplificadores / transmisores de potencia.
- Las guías de ondas se utilizan en instrumentos científicos para medir las propiedades ópticas, acústicas y elásticas de materiales y objetos. La guía de ondas se puede poner en contacto con la muestra (como en una ecografía médica), en cuyo caso la guía de ondas asegura que se conserva la potencia de la onda de prueba, o la muestra puede colocarse dentro de la guía de ondas (como en una medición de constante dieléctrica[8] ), de modo que se puedan probar objetos más pequeños y la precisión sea mejor.
- Las líneas de transmisión son un tipo específico de guía de ondas, de uso muy común.
Tipos de Guías de Onda[editar]
Existen muchos tipos de guías de onda, presentándoles aquí las más importantes:
- Guía de onda rectangular (circular, elíptica): Son aquellas cuya sección transversal es rectangular (circular, elíptica).
- Guía de onda de haz: Guía de Onda constituida por una sucesión de lentes o espejos, capaz de guiar una onda electromagnética.
- Guía de onda tabicada: Formada por dos cilindros metálicos coaxiales unidos en toda su longitud por un tabique radial metálico.
- Guía de onda acanalada, guiada en V; guiada en H:
- Guía de onda rectangular que incluye resaltes conductores interiores a lo largo de una de cada una de las paredes de mayor dimensión.
- Guía de onda carga periódicamente: Guía de onda en las que la propagación viene determinada por las variaciones regularmente espaciadas de las propiedades del medio, de las dimensiones del medio o de las superficie de contorno.
- Guía de onda dieléctrica: Formada íntegramente por uno o varios materiales dieléctricos, sin ninguna pared conductora.
Guía de onda coaxiales[editar]
Las líneas Coaxiales[9] son líneas de transmisión, las cuales consisten en un conductor interno y un revestimiento coaxial externo separado por un medio dieléctrico. Esta estructura ofrece la importante ventaja de confinar completamente los campos eléctrico y magnético dentro de la región dieléctrica, de tal manera que es inmune a las interferencias externas a la línea.
Modos
El principal modo en la línea coaxial es ambos Transversal Eléctrico y Transversal Magnético, es decir, un modo TEM. Una característica ideal es que no tiene longitud de onda de corte y puede propagarse para todas las frecuencias de corriente continua a través de microondas. En práctica, el límite superior es la frecuencia a la cual modos más grandes pueden propagarse. El primer modo alto en la línea coaxial es el modo TE1,1, o modo dominante de una guía de onda circular. Sin embargo la longitud de onda de corte para este modo en la línea coaxial no es la misma como en la guía de onda circular. La longitud de onda de corte aproximada es de:
Donde a es el radio exterior del conductor interno y b es el radio interior del exterior.
Velocidad de fase
La longitud de onda en una línea coaxial es la misma a la longitud de onda en un medio ilimitado que tiene la misma constante dieléctrica; esta es, en una línea coaxial,
Donde es la longitud de onda en el vacío. Luego la velocidad de propagación es,
Donde es la velocidad de la luz. Si el dieléctrico en la línea coaxial es aire, , entonces la velocidad de propagación es la misma que la velocidad de la luz. Una característica importante es que no hay distinción entre velocidad de fase y velocidad de grupo como las hay en las guías de ondas.
Atenuaciones
La atenuación en una línea coaxial, como en otras formas de línea de transmisión, llega desde dos fuentes de pérdidas. Esas son las perdidas por el componente por el cual está hecho el conductor, y la otra es la pérdida del dieléctrico en el medio entre los conductores.
Estudio de reflexiones de señales en líneas de transmisión de cable coaxial
Los cables coaxiales pueden transmitir señales de altas frecuencias y tener distintas impedancias internas dependiendo del material con el cual están compuestos, tanto los conductores, como el dieléctrico.
Por medio de un estudio realizado a partir del envío de una señal eléctrica, se pueden realizar ciertas observaciones acerca de cómo es el comportamiento de esta señal dentro de la línea coaxial.
Al generarse un cortocircuito en el extremo de la misma y mediante el uso de un instrumento se logra medir el momento en que se envió la señal y el momento en que se produjo el regreso de la misma; entonces teniendo el tiempo en el que se produjo el reflejo, y sabiendo la longitud de la línea coaxial, se puede calcular la velocidad de propagación de la información en este medio.
Otra observación a realizar es como distintas guías coaxiales que poseen distintos factores de impedancias, producen reflexiones no deseadas en las uniones de las líneas.
Además si se realizan sucesivas conexión de mismos cables coaxiales, los rebotes que interfieren con la señal original se pueden trasladar en el tiempo, lo suficiente para que se observe a esta señal aislada del rebote producido por las conexiones.
Un hecho que es invariante en las sucesivas modificaciones y extensiones de la línea coaxial, es que el rebote de la línea de transmisión principal, sigue produciéndose en el mismo intervalo de tiempo, lo cual nos muestra que la velocidad de transmisión en la misma solo depende de su impedancia característica.
Un hecho útil de analizar es el estudio de las modificaciones de los rebotes al modificar los valores de impedancia de salida de la línea de transmisión, esto es observable a partir de la conexión de impedancias de distintos valores en la terminación del cable. Una vez realizado la modificación de las impedancias de salida, se puede observar que si el valor de la resistencia es menor que la impedancia característica del cable, la señal reflejada se encuentra en contra fase, mientras que si el valor resistivo es cercano a la impedancia, casi no encontramos un rebote, lo que demuestra que la señal no diferencia el medio.
A medida que el valor de la resistencia conectada aumenta, el valor de la señal reflejada comienza a comportarse de manera asintótica, indicando que a una resistencia lo suficientemente grande, la señal rebota completamente.
Guía de onda acústicas[editar]
Una guía de onda acústica es una estructura física para el guiado de ondas de sonido. Un ducto para la propagación sónica también se comporta como una línea de transmisión. El ducto contiene algún medio, como aire, para soportar la propagación del sonido.
Síntesis del sonido[editar]
El uso de líneas digitales de retardo como elementos computacionales de simulación de propagación de ondas en tubos de Instrumento de viento y en cuerdas vibrantes de instrumentos de cuerdas.
Referencias[editar]
- ↑ Institute of Electrical and Electronics Engineers, “The IEEE standard dictionary of electrical and electronics terms”; 6th ed. New York, N.Y., Institute of Electrical and Electronics Engineers, c1997. IEEE Std 100-1996. ISBN 1-55937-833-6 [ed. Standards Coordinating Committee 10, Terms and Definitions; Jane Radatz, (chair)]
- ↑ ORIENTATION BY MEANS OF LONG RANGE ACOUSTIC SIGNALING IN BALEEN WHALES, R. Payne, D. Webb, in Annals NY Acad. Sci., 188:110-41 (1971)
- ↑ N. W. McLachlan, Theory and Applications of Mathieu Functions, p. 8 (1947) (reprinted by Dover: New York, 1964).
- ↑ The Theory of Sound, by J. W. S. Rayleigh, (1894)
- ↑ Emerson, D. T. (1997). The work of Jagadis Chandra Bose: 100 years of MM-wave research. «1997 IEEE MTT-S International Microwave Symposium Digest». IEEE Transactions on Microwave Theory and Research 45 (12). pp. 2267-2273. Bibcode:1997imsd.conf..553E. ISBN 9780986488511. S2CID 9039614. doi:10.1109/MWSYM.1997.602853. Parámetro desconocido
|citeseerx=ignorado (ayuda) reprinted in Igor Grigorov, Ed., Antentop, Vol. 2, No.3, pp. 87–96. - ↑ Advanced Engineering Electromagnetics Archivado el 14 de mayo de 2009 en Wayback Machine., by C. A. Balanis, John Wiley & Sons (1989).
- ↑ Oliner, pp. 544-548
- ↑ J. R. Baker-Jarvis, "Transmission / reflection and short-circuit line permittivity measurements", NIST tech. note 1341, July 1990
- ↑ Introduction to Microwaves. Gershon J. Wheeler
[1]
Enlaces externos[editar]
- ↑ Error en la cita: Etiqueta
<ref>no válida; no se ha definido el contenido de las referencias llamadasSin-nombre-p3aM-1

































