Factor de empaquetamiento atómico
En cristalografía, el factor de empaquetamiento atómico (FEA), en inglés: atomic packing factor, APF, es la fracción de volumen en una celda unidad que está ocupada por átomos. Este factor es adimensional. Para propósitos prácticos, el FEA de una celda unidad se determina asumiendo que los átomos son esferas rígidas. Con respecto a cristales de un componente (los que contienen un tipo de átomo único), el FEA se representa matemáticamente por:
donde:
- Nátomos , es el número de átomos en la celda unidad,
- Vátomo es el volumen de un átomo, y
- Vcelda unidad es el volumen ocupado por la celda unidad.
Matemáticamente se puede probar que, para estructuras de un componente, el valor del FEA del arreglo más denso de átomos es de alrededor de 0.74. En realidad, debido a factores intermoleculares específicos, esta cifra puede ser mayor. Referente a estructuras de componentes múltiples puede exceder el 0.74.
Ejemplo[editar]


La celda unidad para la estructura cúbica centrada en el cuerpo, en inglés: Body-centered cubic, BCC, contiene dos átomos: un octavo (1/8) de átomo en cada esquina del cubo y un átomo en el centro. Dado que el volumen de cada átomo ubicado en las esquinas es compartido con las celdas adyacentes, cada celda BCC contiene dos átomos.
Cada átomo en las esquinas toca el átomo central. Una línea que sea dibujada desde una esquina del cubo a través del centro hacia la otra esquina pasa a lo largo de 4r, donde r es el radio de un átomo. Por geometría, la longitud de la diagonal es a•√3. Por lo tanto, la longitud de cada lado de la estructura BCC se puede relacionar con el radio de cada átomo mediante la fórmula siguiente:
Conociendo esto y la fórmula del volumen de una esfera: π r3, es posible calcular el FEA, de la siguiente manera:
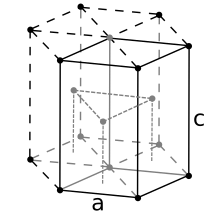
Para la estructura hexagonal la derivación es similar. La longitud de un lado del hexágono se denota por la literal a, y su altura se representa mediante c. Entonces:
Luego es posible calcular el FEA, como sigue:
FEA de estructuras comunes[editar]
Mediante procedimientos similares se pueden calcular los factores de empaquetamiento atómico ideales de todas las estructuras cristalinas. A continuación, se incluyen datos de algunos factores comunes, redondeados a la centésima más próxima.
- Cúbica simple (CS): 0,52
- Cúbica centrada en el cuerpo (BCC): 0,68
- Hexagonal compacta (HCP): 0,74
- Cúbica centrada en las caras (FCC): 0,74
- Cúbica diamante: 0,34
Véase también[editar]
Referencias[editar]
- Schaffer, Saxena, Antolovich, Sanders, and Warner (1999). The Science and Design of Engineering Materials (Second Edition edición). Nueva York: WCB/McGraw-Hill. pp. 81-88.
- Callister, W. (2002). Materials Science and Engineering (Sixth Edition edición). San Francisco: John Wiley and Sons. pp. 105-114.
Enlaces externos[editar]
- Esta obra contiene una traducción total derivada de «Atomic packing factor» de Wikipedia en inglés, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
- Explicación sobre estructura y geometría cristalina
- Empaquetamiento atómico y molecular visto por los cristales.









(c)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/877b73d7beaafe980bd805bfb32e29485936b074)
^{2}({\sqrt {\frac {2}{3}}})(4r)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2eed9cc350feed8da9cf12d57c730c1d06a5a73)
(16r^{3})}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9ae9c749fc06e0902a09ceb3192d4ad45094303)


