Ecuaciones de Fresnel

Las ecuaciones de Fresnel, también conocidas como fórmulas de Fresnel, son un conjunto de relaciones matemáticas que relacionan las amplitudes de las ondas reflejadas y refractadas (o transmitidas) en función de la amplitud de la onda incidente. Su nombre hace honor al físico francés Augustin-Jean Fresnel, quien estudió el comportamiento de la luz al desplazarse entre medios que tienen índices de refracción distintos.
Generalidades[editar]

Cuando una onda electromagnética que se desplaza por un medio caracterizado por un índice de refracción , incide sobre la interfaz con otro medio que posee un índice de refracción , una parte de la onda se refleja y otra porción se transmite al otro medio. Las fórmulas de Fresnel dan una descripción completa y detallada del comportamiento de la onda, tanto en la onda que se refleja como en la onda que se transmite al segundo medio. La dirección de propagación de una onda electromagnética es siempre perpendicular a sus vectores eléctricos y magnéticos, por lo que uno de estos vectores debe estar en el plano de incidencia. Consideraremos que la onda electromagnética está polarizada elípticamente, ésta siempre va a poder expresarse mediante dos vectores perpendiculares en el plano de incidencia. Llamaremos al vector paralelo al plano de incidencia como y al vector perpendicular a éste plano como . Simplificando el problema, sin perder generalidad, podemos describir a estos vectores así:
(1)
donde es la amplitud de la onda de incidencia paralela al plano incidente y viene dado por la expresión: donde es el unitario de la dirección.
(2)
que nos da la dirección del campo magnético.
Relaciones de Fresnel[editar]
En el diagrama, un rayo de luz incidente PO incide en un punto O de la interfaz entre dos medios de índices de refracción n1 y n2. Parte del rayo se refleja formando el rayo OQ y otra parte se refracta formando el rayo OS. Los ángulos que los rayos incidente, reflejado y refractado forman con la normal a la interfaz son θi, θr y θt, respectivamente. La relación entre estos ángulos queda determinada por la ley de reflexión y la ley de Snell.
La fracción de la intensidad de la luz incidente que es reflejada en la interfaz es determinada por el coeficiente de reflexión R, y la fracción refractada es determinada mediante el coeficiente de transmisión T. Las ecuaciones de Fresnel asumen que los dos materiales son paramagnéticos, es decir, poseen una permeabilidad magnética similar a la del vacío. De esta forma, las ecuaciones se pueden usar para calcular R y T.

El cálculo de R y T depende de la polarización del rayo incidente.

- Onda polarizada
- - Si la luz está polarizada en la dirección del campo eléctrico, perpendicular al plano del diagrama, polarizada en s (ver figura 1), el coeficiente de la reflexión viene dado por:
- Donde θt se obtiene de θi por la Ley de Snell
- - Si el rayo está polarizado en paralelo al plano del diagrama, polarizado en p (ver figura 2), R viene dado por:
- EL coeficiente de transmisión en cada caso está dado por:
- Onda no polarizada
- Si la luz no está polarizada, el coeficiente de reflexión es:
Los coeficientes de reflexión y transmisión representan los ratios de intensidad incidente que se reflejan y transmiten respectivamente.
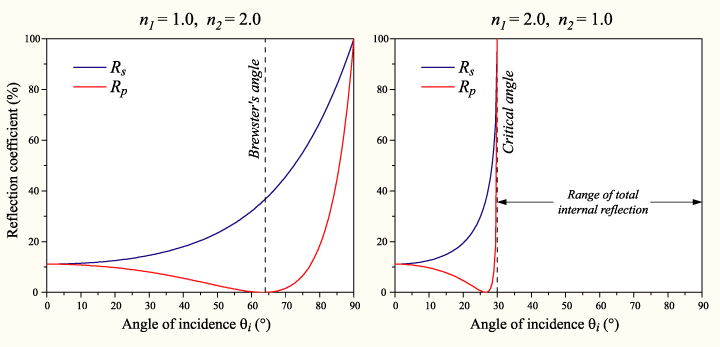
Para unos n1 y n2 dados, existe un ángulo característico para el cual, el valor de RP se hace cero, y una onda incidente, polarizada en P, es totalmente refractada. Este ángulo es conocido como Ángulo de Brewster. Para el vidrio y el aire (o vacío) el valor del Ángulo de Brewster está alrededor de los 56°.
En el caso en que se pasa de un medio de mayor densidad a otro menor (n1 > n2), según se va aumentando el ángulo de incidencia, se llega a un punto en que toda la luz es reflejada. En ángulo de incidencia que forma el rayo, en esta situación, se denomina Ángulo Crítico, y en este punto, RS = RP = 1. Este fenómeno es conocido como Reflexión Interna Total. Para el vidrio-aire, el Ángulo Crítico está en torno a los 41°.
Cuando el rayo incidente es aproximadamente normal a la superficie entre medios, (θi ≈ θt ≈ 0), los coeficientes de reflexión y transmisión esta dados por:
Para el vidrio común, el valor de la reflexión esta alrededor del 4%. No obstante, nótese que la reflexión en una ventana de vidrio, se da tanto en la cara externa como en la interna, y por lo tanto, parte de la luz transmitida vuelve a reflejarse un número indefinido de veces entre las dos caras del vidrio, y con intensidad decreciente. De esta forma, el coeficiente de reflexión combinado, es el límite de la suma infinita de estas reflexiones, y cuyo valor es:
Realmente, cuando la luz hace varias reflexiones entre dos superficies paralelas, los múltiples rayos de luz interfieren unos con otros, y de esta manera, la superficie actúa como un Interferómetro de Fabry-Perot”. Este efecto es el responsable de la coloración que se observa por ejemplo en las películas de aceite sobre el agua. Se aprovecha en óptica para la fabricación de coberturas que pueden disminuir la reflectividad, o que puedan ser usadas como filtro óptico.
NOTA: la discusión dada en este artículo asume que la permeabilidad μ, es igual a la permeabilidad del vacío, μ0, en ambos medios. Esta aproximación es suficiente para la mayoría de los dieléctricos, pero no para otros tipos de material, en los cuales las Ecuaciones de Fresnel son más complicadas.
Véase también[editar]
Referencias[editar]
- Propagación, reflexión y refracción
- Fresnel equations en Eric Weissteins World of Physics
- Fórmulas de Fresnel
Enlaces externos[editar]
- Weisstein, Eric W. «Fresnel Equations». ScienceWorld (en inglés). Wolfram Research.
- FreeSnell – Software libre que calcula las propiedades ópticas de materiales multicapa.
- Thinfilm – Interfaz web para calcular propiedades ópticas de películas delgadas y materiales multicapa. (Coeficientes de reflexión y transmisión, parámetros elipsométricos Psi & Delta)
- Interfaz web simple para calcular ángulos de reflexión y refracción en interfaces e intensidades.












![{\displaystyle {{R}_{S}}={{\left[{\frac {\operatorname {sen}({{\theta }_{t}}-{{\theta }_{i}})}{\operatorname {sen}({{\theta }_{t}}+{{\theta }_{i}})}}\right]}^{2}}={{\left[{\frac {{{n}_{1}}\cos {{\theta }_{i}}-{{n}_{2}}\cos {{\theta }_{t}}}{{{n}_{1}}\cos {{\theta }_{i}}+{{n}_{2}}\cos {{\theta }_{t}}}}\right]}^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e423cc2314d8d3d6659da321da23299e8a659386)
![{\displaystyle {{R}_{P}}={{\left[{\frac {\tan({{\theta }_{t}}-{{\theta }_{i}})}{\tan({{\theta }_{t}}+{{\theta }_{i}})}}\right]}^{2}}={{\left[{\frac {{{n}_{1}}\cos {{\theta }_{t}}-{{n}_{2}}\cos {{\theta }_{i}}}{{{n}_{1}}\cos {{\theta }_{t}}+{{n}_{2}}\cos {{\theta }_{i}}}}\right]}^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dabe90c14325b488bdd41874403db716617d8be1)