Anexo:Constantes matemáticas
El contenido del presente anexo es un listado de constantes matemáticas.
Constantes y funciones matemáticas[editar]
La estructura de la tabla es la siguiente:
- Valor numérico de la constante y enlace a MathWorld o a OEIS Wiki.
- LaTeX: Fórmula o serie en el formato TeX.
- Fórmula: Para utilizar en Wolfram Alpha. Si en los cálculos, ∞ demora mucho tiempo, puede cambiarse por 20000, para obtener un resultado aproximado.
- OEIS: On-Line Encyclopedia of Integer Sequences.
- Fracción continua: En el formato simple [Parte entera; frac1, frac2, frac3, ...] , suprarrayada si es periódica.
- Año: Del descubrimiento de la constante, o datos del autor.
- Formato web: Valor de la constante, en formato adecuado para los buscadores web.
- N.º: Tipo de Número
- R - Racional
- I - Irracional
- A - Algebraico
- T - Trascendental
- C - Complejo
- (La tabla se puede ordenar ascendente o descendente, por cualquiera de los campos, sin más que pulsar en los títulos del encabezado).
| Valor | Nombre | Gráfico | Símbolo | LaTeX | Fórmula | N.º | OEIS | Fracción continua | Año | Formato web |
|---|---|---|---|---|---|---|---|---|---|---|
| 0,08607 13320 55934 20688[Ow 1] | Constante Erdős– Tenenbaum–Ford |
1-(1+log(log(2)))/log(2) | A074738 | [0;11,1,1,1,1,1,1,1,2,3,2,1,4,1,1,10,1,1,8,2,...] | 0.08607133205593420688757309877692267 | |||||
| 1,46557 12318 76768 02665 | Proporción súper áurea [1] |
real root of x^3-x^2-1. | A092526 | [1;4,6,5,5,7,1,2,3,1,8,7,6,7,6,8,0,2,6,6,5,6,...] | 1.46557123187676802665673122521993910 | |||||
| 0,88622 69254 52758 01364[Mw 1] | Factorial de un medio[2] |
sqrt(Pi)/2 | A019704 | [0;1,7,1,3,1,2,1,57,6,1,3,1,37,3,41,1,10,2, ...] | 0.88622692545275801364908374167057259 | |||||
| 0,74048 04896 93061 04116[Mw 2] | Constante de Hermite Empaquetamiento óptimo de esferas 3D Conjetura de Kepler[3] | 
|
Después de 400 años, Thomas Hales demostró en 2014 con El Proyecto Flyspeck, que la Conjetura de Kepler era cierta.[4] | pi/(3 sqrt(2)) | A093825 | [0;1,2,1,5,1,4,2,2,1,1,2,2,2,6,1,1,1,5,2,1,1,1, ...] | 1611 | 0.74048048969306104116931349834344894 | ||
| 1,60669 51524 15291 76378[Mw 3] | Constante de Erdős–Borwein[5][6] | sum[n=1 to ∞] {1/(2^n-1)} |
I | A065442 | [1;1,1,1,1,5,2,1,2,29,4,1,2,2,2,2,6,1,7,1,6,1,2,...] | 1949 | 1.60669515241529176378330152319092458 | |||
| 0,07077 60393 11528 80353 -0,68400 03894 37932 129 i [Ow 2] |
Constante MKB [7]·[8]·[9] |
lim_(2n->∞) int[1 to 2n] {exp(i*Pi*x)*x^(1/x) dx} |
C | A255727 A255728 |
[0;14,7,1,2,1,23,2,1,8,16,1,1,3,1,26,1,6,1,1, ...] - [0;1,2,6,13,41,112,1,25,1,1,1,1,3,13,2,1, ...] i |
2009 | 0.07077603931152880353952802183028200 -0.68400038943793212918274445999266 i | |||
| 3,05940 74053 42576 14453[Mw 4][Ow 3] | Constante Doble factorial |

|
Sum[n=0 to ∞]{1/n!!} | A143280 | [3;16,1,4,1,66,10,1,1,1,1,2,5,1,2,1,1,1,1,1,2,...] | 3.05940740534257614453947549923327861 | ||||
| 0,62481 05338 43826 58687 + 1,30024 25902 20120 419 i |
Fracción continua generalizada de i | i+i/(i+i/(i+i/(i+i/(i+i/(i+i/(i+i/( i+i/(i+i/(i+i/(i+i/(i+i/(i+i/(i+i/( i+i/(i+i/(i+i/(i+i/(i+i/(i+i/(i+i/( ...))))))))))))))))))))) |
C A | A156590 A156548 |
[i;1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1, ..] = [0;1,i] |
0.62481053384382658687960444744285144 + 1.30024259022012041915890982074952 i | ||||
| 0,91893 85332 04672 74178[Mw 5] | Fórmula de Raabe[10] | integral_a^(a+1) {log(Gamma(x))+a-a log(a)} dx | A075700 | [0;1,11,2,1,36,1,1,3,3,5,3,1,18,2,1,1,2,2,1,1,...] | 0.91893853320467274178032973640561763 | |||||
| 0,42215 77331 15826 62702[Mw 6] | Volumen del Tetraedro de Reuleaux[11] | 
|
(3*Sqrt[2] - 49*Pi + 162*ArcTan[Sqrt[2]])/12 | A102888 | [0;2,2,1,2,2,7,4,4,287,1,6,1,2,1,8,5,1,1,1,1, ...] | 0.42215773311582662702336591662385075 | ||||
| 1,17628 08182 59917 50654[Mw 7] | Constante de Salem, conjetura de Lehmer[12] | x^10+x^9-x^7-x^6-x^5-x^4-x^3+x+1 | A | A073011 | [1;5,1,2,17,1,7,2,1,1,2,4,7,2,2,1,1,15,1,1, ... | 1983? | 1.17628081825991750654407033847403505 | |||
| 2,39996 32297 28653 32223[Mw 8] |
Ángulo áureo[13] |  |
= 137.507764050037854646 ...° | (4-2*Phi)*Pi | T | A131988 | [2;2,1,1,1087,4,4,120,2,1,1,2,1,1,7,7,2,11,...] | 1907 | 2.39996322972865332223155550663361385 | |
| 1,26408 47353 05301 11307[Mw 9] | Constante de Vardi[14] | A076393 | [1;3,1,3,1,2,5,54,7,1,2,1,2,3,15,1,2,1,1,2,1,...] | 1991 | 1.26408473530530111307959958416466949 | |||||
| 1,5065918849 ± 0,0000000028[Mw 10] | Área del fractal de Mandelbrot[15] | 
|
Se conjetura que el valor exacto es: = 1,506591651... | A098403 | [1;1,1,37,2,2,1,10,1,1,2,2,4,1,1,1,1,5,4,...] | 1912 | 1.50659177 +/- 0.00000008 | |||
1,61111 49258 08376 736 111•••111 27224 36828[Mw 11] 183213 unos |
Constante Factorial exponencial |
T | A080219 | [1; 1, 1, 1, 1, 2, 1, 808, 2, 1, 2, 1, 14,...] | 1.61111492580837673611111111111111111 | |||||
| 0,31813 15052 04764 13531 ±1,33723 57014 30689 40 i [Ow 4] |
Punto fijo Super-logaritmo[16]·[17] |

|
Para un valor inicial de x distinto a 0, 1, e, e^e, e^(e^e), etc. |
-W(-1) Donde W=ProductLog Lambert W function |
C | A059526 A059527 |
[-i;1 +2i,1+i,6-i,1+2i,-7+3i,2i,2,1-2i,-1+i,-, ...] | 0.31813150520476413531265425158766451 -1.33723570143068940890116214319371 i | ||
| 1,09317 04591 95490 89396[Mw 12] | Constante de Smarandache 1.ª [18] | La función Kempner μ(n) se define como sigue:
μ(n) es el número más pequeño por el que μ(n)! es divisible por n |
A048799 | [1;10,1,2,1,2,1,13,3,1,6,1,2,11,4,6,2,15,1,1,...] | 1.09317045919549089396820137014520832 | |||||
| 1,64218 84352 22121 13687[Mw 13] | Constante de Lebesgue L2[19] | 1/5 + sqrt(25 - 2*sqrt(5))/Pi |
T | A226655 | [1;1,1,1,3,1,6,1,5,2,2,3,1,2,7,1,3,5,2,2,1,1,...] | 1910 | 1.64218843522212113687362798892294034 | |||
| 0,82699 33431 32688 07426[Mw 14] | Disk Covering[20] | 
|
3 Sqrt[3]/(2 Pi) | T | A086089 | [0;1,4,1,3,1,1,4,1,2,2,1,1,7,1,4,4,2,1,1,1,1,...] | 1939 1949 |
0.82699334313268807426698974746945416 | ||
| 1,78723 16501 82965 93301[Mw 15] | Constante de Komornik–Loreti[21] |
t k = Sucesión de Thue-Morse |
FindRoot[(prod[n=0 to ∞] {1-1/(x^2^n)}+ (x-2)/(x-1))= 0, {x, 1.7}, WorkingPrecision->30] |
T | A055060 | [1;1,3,1,2,3,188,1,12,1,1,22,33,1,10,1,1,7,...] | 1998 | 1.78723165018296593301327489033700839 | ||
| 0,59017 02995 08048 11302[Mw 16] | Constante de Chebyshev[22] ·[23] | (Gamma(1/4)^2) /(4 pi^(3/2)) |
A249205 | [0;1,1,2,3,1,2,41,1,6,5,124,5,2,2,1,1,6,1,2,...] | 0.59017029950804811302266897027924429 | |||||
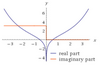
| 0,52382 25713 89864 40645[Mw 17] | Función Chi Coseno hiperbólico integral |
|
|
Chi(x) | A133746 | [0;1,1,9,1,172,1,7,1,11,1,1,2,1,8,1,1,1,1,1,...] | 0.52382257138986440645095829438325566 | |||
| 0,62432 99885 43550 87099[Mw 18] | Constante de Golomb–Dickman[24] | N[Int{n,0,1}[e^Li(n)],34] | A084945 | [0;1,1,1,1,1,22,1,2,3,1,1,11,1,1,2,22,2,6,1,...] | 1930 y 1964 |
0.62432998854355087099293638310083724 | ||||
| 0,98770 03907 36053 46013[Mw 19] | Área delimitada por la rotación excéntrica del Triángulo de Reuleaux[25] |

|
donde a= lado del cuadrado | 2 sqrt(3)+pi/6-3 | T | A066666 | [0;1,80,3,3,2,1,1,1,4,2,2,1,1,1,8,1,2,10,1,2,...] | 1914 | 0.98770039073605346013199991355832854 | |
| 0,70444 22009 99165 59273 | Constante Carefree2 [26] | N[prod[n=1 to ∞] {1 - 1/(prime(n)* (prime(n)+1))}] |
A065463 | [0;1,2,2,1,1,1,1,4,2,1,1,3,703,2,1,1,1,3,5,1,...] | 0.70444220099916559273660335032663721 | |||||
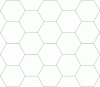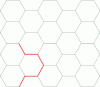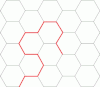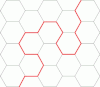
| 1,84775 90650 22573 51225[Mw 20] | Constante camino auto-evitante en red hexagonal[27] ·[28] |
|
La menor raíz real de |
sqrt(2+sqrt(2)) | A | A179260 | [1;1,5,1,1,3,6,1,3,3,10,10,1,1,1,5,2,3,1,1,3,...] | 1.84775906502257351225636637879357657 | ||
| 0,19452 80494 65325 11361[Mw 21] | 2.ª Constante Du Bois Reymond[29] | (e^2-7)/2 | T | A062546 | [0;5,7,9,11,13,15,17,19,21,23,25,27,29,31,...] = [0;2p+3], p∈ℕ |
0.19452804946532511361521373028750390 | ||||
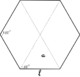
| 2,59807 62113 53315 94029[Mw 22] | Área de un hexágono de lado unitario[30] |
|
3 sqrt(3)/2 | A | A104956 | [2;1,1,2,20,2,1,1,4,1,1,2,20,2,1,1,4,1,1,2,20,...] [2;1,1,2,20,2,1,1,4] |
2.59807621135331594029116951225880855 | |||
| 1,78657 64593 65922 46345[Mw 23] | Constante de Silverman[31] |
|
Sum[n=1 to ∞] {1/[EulerPhi(n) DivisorSigma(1,n)]} |
A093827 | [1;1,3,1,2,5,1,65,11,2,1,2,13,1,4,1,1,1,2,5,4,...] | 1.78657645936592246345859047554131575 | ||||
| 1,46099 84862 06318 35815[Mw 24] | Constante cuatro-colores de Baxter[32] |
Mapamundi |
|
3×Gamma(1/3) ^3/(4 pi^2) |
A224273 | [1;2,5,1,10,8,1,12,3,1,5,3,5,8,2,1,23,1,2,161,...] | 1970 | 1.46099848620631835815887311784605969 | ||
| 0,66131 70494 69622 33528[Mw 25] | Constante de Feller-Tornier[33] |
[prod[n=1 to ∞] {1-2/prime(n)^2}] /2 + 1/2 |
T ? | A065493 | [0;1,1,1,20,9,1,2,5,1,2,3,2,3,38,8,1,16,2,2,...] | 1932 | 0.66131704946962233528976584627411853 | |||
| 1,92756 19754 82925 30426[Mw 26] | Constante Tetranacci | La mayor raíz real de | Root[x+x^-4-2=0] | A | A086088 | [1;1,12,1,4,7,1,21,1,2,1,4,6,1,10,1,2,2,1,7,1,...] | 1.92756197548292530426190586173662216 | |||
| 1,00743 47568 84279 37609[Mw 27] | Constante DeVicci's Teseracto | 
|
Arista del mayor cubo, dentro de un hipercubo unitario 4D.
La menor raíz real de |
Root[4*x^8-28*x^6 -7*x^4+16*x^2+16 =0] |
A | A243309 | [1;134,1,1,73,3,1,5,2,1,6,3,11,4,1,5,5,1,1,48,...] | 1.00743475688427937609825359523109914 | ||
| 0,15915 49430 91895 33576[Mw 28] | Constante A de Plouffe[34] | 1/(2 pi) | T | A086201 | [0;6,3,1,1,7,2,146,3,6,1,1,2,7,5,5,1,4,1,2,42,...] | 0.15915494309189533576888376337251436 | ||||
| 0,41245 40336 40107 59778[Mw 29] | Constante de Thue-Morse[35] |

|
donde es la secuencia Thue–Morse y donde |
T | A014571 | [0;2,2,2,1,4,3,5,2,1,4,2,1,5,44,1,4,1,2,4,1,1,...] | 0.41245403364010759778336136825845528 | |||
| 0,58057 75582 04892 40229[Mw 30] | Constante de Pell[36] | N[1-prod[n=0 to ∞] {1-1/(2^(2n+1)}] |
T ? | A141848 | [0;1,1,2,1,1,1,1,14,1,3,1,1,6,9,18,7,1,27,1,1,...] | 0.58057755820489240229004389229702574 | ||||
| 2,20741 60991 62477 96230[Mw 31] | Problema moviendo el sofá de Hammersley[37] | 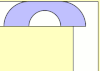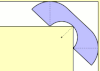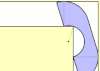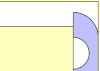
|
¿Cuál es el área más grande de una forma, que pueda ser maniobrada en un pasillo en forma de L y tenga de ancho la unidad ? | pi/2 + 2/pi | T | A086118 | [2;4,1,4,1,1,2,5,1,11,1,1,5,1,6,1,3,1,1,1,1,7,...] | 1967 | 2.20741609916247796230685674512980889 | |
| 1,15470 05383 79251 52901[Mw 32] | Constante de Hermite[38] | 2/sqrt(3) | A | 1+ A246724 |
[1;6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,...] [1;6,2] |
1.15470053837925152901829756100391491 | ||||
| 0,63092 97535 71457 43709[Mw 33] | Dimensión fractal del Conjunto de Cantor[39] | 
|
log(2)/log(3) N[3^x=2] |
T | A102525 | [0;1,1,1,2,2,3,1,5,2,23,2,2,1,1,55,1,4,3,1,1,...] | 0.63092975357145743709952711434276085 | |||
| 0,17150 04931 41536 06586[Mw 34] | Constante Hall-Montgomery[40] |
1 + Pi^2/6 + 2*PolyLog[2, -Sqrt[E]] | A143301 | [0;5,1,4,1,10,1,1,11,18,1,2,19,14,1,51,1,2,1,...] | 0.17150049314153606586043997155521210 | |||||
| 1,55138 75245 48320 39226[Mw 35] | Constante Triángulo Calabi[41] |

|
FindRoot[ 2x^3-2x^2-3x+2 ==0, {x, 1.5}, WorkingPrecision->40] |
A | A046095 | [1;1,1,4,2,1,2,1,5,2,1,3,1,1,390,1,1,2,11,6,2,...] | 1946 ~ | 1.55138752454832039226195251026462381 | ||
| 0,97027 01143 92033 92574[Mw 36] | Constante de Lochs[42] | 6*ln(2)*ln(10)/Pi^2 | A086819 | [0;1,32,1,1,1,2,1,46,7,2,7,10,8,1,71,1,37,1,1,...] | 1964 | 0.97027011439203392574025601921001083 | ||||
| 1,30568 67 ≈ [Mw 37] | Dimensión fractal del círculo de Apolonio[43] | 
|
A052483 | [0;3,2,3,16,8,10,3,1,1,2,1,3,1,2,13,1,1,4,1,5,...] | 1.3056867 ≈ | |||||
| 0,00131 76411 54853 17810[Mw 38] | Constante de Heath-Brown–Moroz[44] | N[prod[n=1 to ∞] {((1-1/prime(n))^7) *(1+(7*prime(n)+1) /(prime(n)^2))}] |
T ? | A118228 | [0;758,1,13,1,2,3,56,8,1,1,1,1,1,143,1,1,1,2,...] | 0.00131764115485317810981735232251358 | ||||
| 0,14758 36176 50433 27417[Mw 39] | Constante gamma de Plouffe[45] | 
|
Arctan(1/2)/Pi | T | A086203 | [0;6,1,3,2,5,1,6,5,3,1,1,2,1,1,2,3,1,2,3,2,2,...] | 0.14758361765043327417540107622474052 | |||
| 0,70523 01717 91800 96514[Mw 40] | Constante Primorial Suma de inversos de productos de primos [46] |
Sum[k=1 to ∞](prod[n=1 to k]{1/prime(n)}) | I | A064648 | [0;1,2,2,1,1,4,1,2,1,1,6,13,1,4,1,16,6,1,1,4,...] | 0.70523017179180096514743168288824851 | ||||
| 0,29156 09040 30818 78013[Mw 41] | Constante dimer 2D, recubrimiento con dominós[47] ·[48] |

|
N[int[-pi to pi] {arccosh(sqrt( cos(t)+3)/sqrt(2)) /(4*Pi) /, dt}] |
A143233 | [0;3,2,3,16,8,10,3,1,1,2,1,3,1,2,13,1,1,4,1,5,...] | 0.29156090403081878013838445646839491 | ||||
| 0,72364 84022 98200 00940[Mw 42] | Constante de Sarnak | N[prod[k=2 to ∞] {1-(prime(k)+2) /(prime(k)^3)}] |
T ? | A065476 | [0;1,2,1,1,1,1,1,1,1,4,4,1,1,1,1,1,1,1,8,2,1,1,...] | 0.72364840229820000940884914980912759 | ||||
| 0,63212 05588 28557 67840[Mw 43] | Constante de tiempo[49] | 
|
|
lim_(n->∞) (1- !n/n!) !n=subfactorial |
T | A068996 | [0;1,1,1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,...] = [0;1,1,1,2n], n∈ℕ |
0.63212055882855767840447622983853913 | ||
| 0.30366 30028 98732 65859[Mw 44] | Constante de Gauss-Kuzmin-Wirsing[50] |
donde es una función analítica tal que . |
A038517 | [0;3,3,2,2,3,13,1,174,1,1,1,2,2,2,1,1,1,2,2,1,...] | 1973 | 0.30366300289873265859744812190155623 | ||||
| 1,30357 72690 34296 39125[Mw 45] | Constante de Conway[51] | 
|
A | A014715 | [1;3,3,2,2,54,5,2,1,16,1,30,1,1,1,2,2,1,14,1,...] | 1987 | 1.30357726903429639125709911215255189 | |||
| 1,18656 91104 15625 45282[Mw 46] | Constante de Lévy[52] | pi^2 /(12 ln 2) | A100199 | [1;5,2,1,3,1,1,28,18,16,3,2,6,2,6,1,1,5,5,9,...] | 1935 | 1.18656911041562545282172297594723712 | ||||
| 0,83564 88482 64721 05333 | Constante de Baker[53] | 
|
Sum[n=0 to ∞] {((-1)^(n))/(3n+1)} |
A113476 | [0;1,5,11,1,4,1,6,1,4,1,1,1,2,1,3,2,2,2,2,1,3,...] | 0.83564884826472105333710345970011076 | ||||
| 23,10344 79094 20541 6160[Mw 47] | Serie de Kempner(0)[54] |
|
1+1/2+1/3+1/4+1/5 +1/6+1/7+1/8+1/9 +1/11+1/12+1/13 +1/14+1/15+... |
A082839 | [23;9,1,2,3244,1,1,5,1,2,2,8,3,1,1,6,1,84,1,...] | 23.1034479094205416160340540433255981 | ||||
| 0,98943 12738 31146 95174[Mw 48] | Constante de Lebesgue[55] | 
|
4/pi^2*[(2 Sum[k=1 to ∞] {ln(k)/(4*k^2-1)}) -poligamma(1/2)] |
A243277 | [0;1,93,1,1,1,1,1,1,1,7,1,12,2,15,1,2,7,2,1,5,...] | 0.98943127383114695174164880901886671 | ||||
| 1,38135 64445 18497 79337 | Constante Beta Kneser-Mahler[56] | e^((PolyGamma(1,4/3) - PolyGamma(1,2/3) +9)/(4*sqrt(3)*Pi)) |
A242710 | [1;2,1,1,1,1,1,4,1,139,2,1,3,5,16,2,1,1,7,2,1,...] | 1963 | 1.38135644451849779337146695685062412 | ||||
| 1,18745 23511 26501 05459[Mw 49] | Constante de Foias α[57] |
La constante de Foias es el único número real tal que si x1 = α, entonces la secuencia diverge a ∞. Cuando x1 = α, |
A085848 | [1;5,2,1,81,3,2,2,1,1,1,1,1,6,1,1,3,1,1,4,3,2,...] | 1970 | 1.18745235112650105459548015839651935 | ||||
| 2,29316 62874 11861 03150[Mw 50] | Constante de Foias β | 
|
x^(x+1) = (x+1)^x |
A085846 | [2;3,2,2,3,4,2,3,2,130,1,1,1,1,1,6,3,2,1,15,1,...] | 2000 | 2.29316628741186103150802829125080586 | |||
| 0,66170 71822 67176 23515[Mw 51] | Constante de Robbins[58] | (4+17*2^(1/2)-6 *3^(1/2)+21*ln(1+ 2^(1/2))+42*ln(2+ 3^(1/2))-7*Pi)/105 |
A073012 | [0;1,1,1,21,1,2,1,4,10,1,2,2,1,3,11,1,331,1,4,...] | 1978 | 0.66170718226717623515583113324841358 | ||||
| 0,78853 05659 11508 96106[Mw 52] | Constante de Lüroth[59] | Sum[n=2 to ∞] log(n/(n-1))/n |
A085361 | [0;1,3,1,2,1,2,4,1,127,1,2,2,1,3,8,1,1,2,1,16,...] | 0.78853056591150896106027632216944432 | |||||
| 0,92883 58271[Mw 53] | Constante entre primos gemelos de JJGJJG[60] | 1/4 + 1/6 + 1/12 + 1/18 + 1/30 + 1/42 + 1/60 + 1/72 + ... | A241560 | [0; 1, 13, 19, 4, 2, 3, 1, 1] | 2014 | 0.928835827131 | ||||
| 5,24411 51085 84239 62092[Mw 54] | Constante 2 Lemniscata[61] |
 |
Gamma[ 1/4 ]^2 /Sqrt[ 2 Pi ] |
A064853 | [5;4,10,2,1,2,3,29,4,1,2,1,2,1,2,1,4,9,1,4,1,2,...] | 1718 | 5.24411510858423962092967917978223883 | |||
| 0,57595 99688 92945 43964[Mw 55] | Constante Stephens[62] | Prod[n=1 to ∞] {1-prime(n) /(prime(n)^3-1)} |
T ? | A065478 | [0;1,1,2,1,3,1,3,1,2,1,77,2,1,1,10,2,1,1,1,7,...] | ? | 0.57595996889294543964316337549249669 | |||
| 0,73908 51332 15160 64165[Mw 56] | Número de Dottie[63] | 
|
cos(c)=c | T | A003957 | [0;1,2,1,4,1,40,1,9,4,2,1,15,2,12,1,21,1,17,...] | 0.73908513321516064165531208767387340 | |||
| 0,67823 44919 17391 97803[Mw 57] | Constante Taniguchi[64] |
|
Prod[n=1 to ∞] {1 -3/prime(n)^3 +2/prime(n)^4 +1/prime(n)^5 -1/prime(n)^6} |
T ? | A175639 | [0;1,2,9,3,1,2,9,11,1,13,2,15,1,1,1,2,4,1,1,1,...] | ? | 0.67823449191739197803553827948289481 | ||
| 1,35845 62741 82988 43520[Mw 58] | Constante espiral áurea | 
|
GoldenRatio^(2/Pi) | A212224 | [1;2,1,3,1,3,10,8,1,1,8,1,15,6,1,3,1,1,2,3,1,1,...] | 1.35845627418298843520618060050187945 | ||||
| 2,79128 78474 77920 00329 | Raíces anidadas S5 |
|
(sqrt(21)+1)/2 | A | A222134 | [2;1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,...] [2;1,3] |
2.79128784747792000329402359686400424 | |||
| 1,85407 46773 01371 91843[Mw 59] | Constante Lemniscata de Gauss[65] | 
|
|
pi^(3/2)/(2 Gamma(3/4)^2) | A093341 | [1;1,5,1,5,1,3,1,6,2,1,4,16,3,112,2,1,1,18,1,...] | ? | 1.85407467730137191843385034719526005 | ||
| 1,75874 36279 51184 82469 | Constante Producto infinito, con Alladi-Grinstead[66] | Prod[n=2 to ∞] {(1+1/n)^(1/n)} |
A242623 | [1;1,3,6,1,8,1,4,3,1,4,1,1,1,6,5,2,40,1,387,2,...] | 1977 | 1.75874362795118482469989684865589317 | ||||
| 1,73245 47146 00633 47358[Ow 5] | Constante inversa de Euler-Mascheroni | 1/Integrate_ (x=0 to 1) {-log(log(1/x))} |
A098907 | [1;1,2,1,2,1,4,3,13,5,1,1,8,1,2,4,1,1,40,1,11,...] | 1.73245471460063347358302531586082968 | |||||
| 1,94359 64368 20759 20505[Mw 60] | Constante Euler Totient[67][68] |

|
zeta(2)*zeta(3) /zeta(6) |
A082695 | [1;1,16,1,2,1,2,3,1,1,3,2,1,8,1,1,1,1,1,1,1,32,...] | 1750 | 1.94359643682075920505707036257476343 | |||
| 1,49534 87812 21220 54191 | Raíz cuarta de cinco[69] | (5(5(5(5(5(5(5) ^1/5)^1/5)^1/5) ^1/5)^1/5)^1/5) ^1/5 ... |
A | A011003 | [1;2,53,4,96,2,1,6,2,2,2,6,1,4,1,49,17,2,3,2,...] | 1.49534878122122054191189899414091339 | ||||
| 0,87228 40410 65627 97617[Mw 61] | Área Círculo de Ford[70] | 
|
|
pi Zeta(3) /(4 Zeta(4)) | [0;1,6,1,4,1,7,5,36,3,29,1,1,10,3,2,8,1,1,1,3,...] | ? | 0.87228404106562797617519753217122587 | |||
| 1,08232 32337 11138 19151[Mw 62] | Constante Zeta(4)[71] | Sum[n=1 to ∞] {1/n^4} |
T | A013662 | [1;12,6,1,3,1,4,183,1,1,2,1,3,1,1,5,4,2,7,...] | 1.08232323371113819151600369654116790 | ||||
| 1,56155 28128 08830 27491 | Raíz Triangular de 2.[72] | 
|
|
(sqrt(17)-1)/2 | A | A222133 | [1;1,1,3,1,1,3,1,1,3,1,1,3,1,1,3,1,1,3,1,1,3,1,...] [1;1,1,3] |
1.56155281280883027491070492798703851 | ||
| 1,45607 49485 82689 67139[Mw 63] | Constante de Backhouse[73] |
|
1/( FindRoot[0 == 1 + Sum[x^n Prime[n], {n, 10000}], {x, {1}}) |
A072508 | [1;2,5,5,4,1,1,18,1,1,1,1,1,2,13,3,1,2,4,16,4,...] | 1995 | 1.45607494858268967139959535111654355 | |||
| 1,43599 11241 76917 43235[Mw 64] | Constante interpolación de Lebesgue[74] ·[75] | 
|
1/3 + 2*sqrt(3)/Pi | T | A226654 | [1;2,3,2,2,6,1,1,1,1,4,1,7,1,1,1,2,1,3,1,2,1,1,...] | 1902 ~ | 1.43599112417691743235598632995927221 | ||
| 1,04633 50667 70503 18098 | Constante mass Minkowski-Siegel[76] | N[prod[n=1 to ∞] n! /(sqrt(2*Pi*n) *(n/e)^n *(1+1/n) ^(1/12))] |
A213080 | [1;21,1,1,2,1,1,4,2,1,5,7,2,1,20,1,1,1134,3,..] | 1867 1885 1935 |
1.04633506677050318098095065697776037 | ||||
| 1,86002 50792 21190 30718 | Constante espiral de Theodorus[77] |

|
Sum[n=1 to ∞] {1/(n^(3/2) +n^(1/2))} |
A226317 | [1;1,6,6,1,15,11,5,1,1,1,1,5,3,3,3,2,1,1,2,19,...] | -460 a -399 |
1.86002507922119030718069591571714332 | |||
| 0,80939 40205 40639 13071[Mw 65] | Constante de Alladi-Grinstead[78] | e^{(sum[k=2 to ∞] |sum[n=1 to ∞] {1/(n k^(n+1))})-1} |
A085291 | [0;1,4,4,17,4,3,2,5,3,1,1,1,1,6,1,1,2,1,22,...] | 1977 | 0.80939402054063913071793188059409131 | ||||
| 1,26185 95071 42914 87419[Mw 66] | Dimensión fractal del Copo de nieve de Koch[79] | log(4)/log(3) | T | A100831 | [1;3,1,4,1,1,11,1,46,1,5,112,1,1,1,1,1,3,1,7,...] | 1.26185950714291487419905422868552171 | ||||
| 1,22674 20107 20353 24441[Mw 67] | Constante Factorial de Fibonacci[80] | prod[n=1 to ∞] {1-((sqrt(5) -3)/2)^n} |
A062073 | [1;4,2,2,3,2,15,9,1,2,1,2,15,7,6,21,3,5,1,23,...] | 1.22674201072035324441763023045536165 | |||||
| 0,85073 61882 01867 26036[Mw 68] | Constante de plegado de papel[81] ·[82] | 
|
N[Sum[n=0 to ∞] {8^2^n/(2^2^ (n+2)-1)},37] |
A143347 | [0;1,5,1,2,3,21,1,4,107,7,5,2,1,2,1,1,2,1,6,...] | ? | 0.85073618820186726036779776053206660 | |||
| 6,58088 59910 17920 97085 | Constante de Froda[83] | 2^e | [6;1,1,2,1,1,2,3,1,14,11,4,3,1,1,7,5,5,2,7,...] | 6.58088599101792097085154240388648649 | ||||||
| – 0,5 ± 0,86602 54037 84438 64676 i |
Raíz cúbica de 1[84] | 
|
1, E^(2i pi/3) , E^(-2i pi/3) |
CA | A010527 | - [0,5] ± [0;1,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,...] i - [0,5] ± [0; 1, 6, 2] i |
- 0,5 ± 0.8660254037844386467637231707529 i | |||
| 1,11786 41511 89944 97314[Mw 69] | Constante de Goh-Schmutz[85] | Integrate{ log(s+1) /(E^s-1)} |
A143300 | [1;8,2,15,2,7,2,1,1,1,1,2,3,5,3,5,1,1,4,13,1,...] | 1.11786415118994497314040996202656544 | |||||
| 1,11072 07345 39591 56175[Mw 70] | Razón entre un cuadrado y la circunferencia circunscrita[86] | 
|
Sum[n=1 to ∞] {(-1)^(floor((n-1)/2)) /(2n-1)} |
T | A093954 | [1;9,31,1,1,17,2,3,3,2,3,1,1,2,2,1,4,9,1,3,...] | 1.11072073453959156175397024751517342 | |||
| 2,82641 99970 67591 57554[Mw 71] | Constante de Murata[87] | Prod[n=1 to ∞] {1+1/(prime(n) -1)^2} |
T ? | A065485 | [2;1,4,1,3,5,2,2,2,4,3,2,1,3,2,1,1,1,8,2,2,28,...] | 2.82641999706759157554639174723695374 | ||||
| 1,52362 70862 02492 10627[Mw 72] | Dimensión fractal de la frontera de la Curva del dragón[88] | 
|
(log((1+(73-6 sqrt(87))^1/3+ (73+6 sqrt(87))^1/3) /3))/ log(2))) |
T | [1;1,1,10,12,2,1,149,1,1,1,3,11,1,3,17,4,1,...] | 1.52362708620249210627768393595421662 | ||||
| 1,30637 78838 63080 69046[Mw 73] | Constante de Mills[89] | Es primo | Nest[ NextPrime[#^3] &, 2, 7]^(1/3^8) | A051021 | [1;3,3,1,3,1,2,1,2,1,4,2,35,21,1,4,4,1,1,3,2,...] | 1947 | 1.30637788386308069046861449260260571 | |||
| 2,02988 32128 19307 25004[Mw 74] | Volumen hiperbólico del Complemento del Nudo en Forma de Ocho[90] | 
|
|
6 integral[0 to pi/3] {log(1/(2 sin (n)))} |
A091518 | [2;33,2,6,2,1,2,2,5,1,1,7,1,1,1,113,1,4,5,1,...] | 2.02988321281930725004240510854904057 | |||
| 1,46707 80794 33975 47289[Mw 75] | Constante de Porter[91] |
|
6*ln2/Pi^2(3*ln2+ 4 EulerGamma- WeierstrassZeta'(2) *24/Pi^2-2)-1/2 | A086237 | [1;2,7,10,1,2,38,5,4,1,4,12,5,1,5,1,2,3,1,...] | 1974 | 1.46707807943397547289779848470722995 | |||
| 1,85193 70519 82466 17036[Mw 76] | Constante de Gibbs[92] | 
|
Integral senoidal |
|
SinIntegral[Pi] | A036792 | [1;1,5,1,3,15,1,5,3,2,7,2,1,62,1,3,110,1,39,...] | 1.85193705198246617036105337015799136 | ||
| 1,78221 39781 91369 11177[Mw 77] | Constante de Grothendieck[93] | pi/(2 log(1+sqrt(2))) | A088367 | [1;1,3,1,1,2,4,2,1,1,17,1,12,4,3,5,10,1,1,3,...] | 1.78221397819136911177441345297254934 | |||||
| 1,74540 56624 07346 86349[Mw 78] | Constante media armónica de Khinchin[94] | 
|
a1...an son elementos de una fracción continua [a0;a1,a2,...,an] |
(log 2)/ (sum[n=1 to ∞] {1/n log(1+ 1/(n(n+2))} |
A087491 | [1;1,2,1,12,1,5,1,5,13,2,13,2,1,9,1,6,1,3,1,...] | 1.74540566240734686349459630968366106 | |||
| 0,10841 01512 23111 36151[Mw 79] | Constante de Trott[95] |
|
Trott Constant | A039662 | [0;9,4,2,5,1,2,2,3,1,1,1,3,6,1,5,1,1,2,...] | 0.10841015122311136151129081140641509 | ||||
| 1,45136 92348 83381 05028[Mw 80] | Constante de Ramanujan–Soldner[96] ·[97] | 
|
|
FindRoot[li(x) = 0] | I | A070769 | [1;2,4,1,1,1,3,1,1,1,2,47,2,4,1,12,1,1,2,2,1,...] | 1792 a 1809 |
1.45136923488338105028396848589202744 | |
| 0,64341 05462 88338 02618[Mw 81] | Constante de Cahen[98] |
sk son términos de la Sucesión de Sylvester 2, 3, 7, 43, 1807 ...
|
T | A118227 | [0; 1, 1, 1, 4, 9, 196, 16641, 639988804, ...] | 1891 | 0.64341054628833802618225430775756476 | |||
| -4,22745 35333 76265 408[Mw 82] | Digamma (¼)[99] | 
|
-EulerGamma -\pi/2 -3 log 2 |
A020777 | -[4;4,2,1,1,10,1,5,9,11,1,22,1,1,14,1,2,1,4,...] | -4,2274535333762654080895301460966835 | ||||
| 1,77245 38509 05516 02729[Mw 83] | Constante de Carlson-Levin[100] | sqrt (pi) | T | A002161 | [1;1,3,2,1,1,6,1,28,13,1,1,2,18,1,1,1,83,1,...] | 1.77245385090551602729816748334114518 | ||||
| 0,23571 11317 19232 93137[Mw 84] | Constante de Copeland-Erdős[101] | sum[n=1 to ∞] {prime(n) /(n+(10^ sum[k=1 to n]{floor (log_10 prime(k))}))} |
I | A033308 | [0;4,4,8,16,18,5,1,1,1,1,7,1,1,6,2,9,58,1,3,...] | 0.23571113171923293137414347535961677 | ||||
| 2,09455 14815 42326 59148[Mw 85] | Constante de Wallis[102] | 
|
(((45-sqrt(1929)) /18))^(1/3)+ (((45+sqrt(1929)) /18))^(1/3) |
A | A007493 | [2;10,1,1,2,1,3,1,1,12,3,5,1,1,2,1,6,1,11,4,...] | 1616 a 1703 |
2.09455148154232659148238654057930296 | ||
| 0,28674 74284 34478 73410[Mw 86] | Constante Strongly Carefree[103] | N[ prod[k=1 to ∞] {1 - (3*prime(k)-2) /(prime(k)^3)}] |
A065473 | [0;3,2,19,3,12,1,5,1,5,1,5,2,1,1,1,1,1,3,7,...] | 0.28674742843447873410789271278983845 | |||||
| 0,56714 32904 09783 87299[Mw 87] | Constante Omega, función W(1) de Lambert[104] | 
|
Sum[n=1 to ∞] {(-n)^(n-1)/n!} |
T | A030178 | [0;1,1,3,4,2,10,4,1,1,1,1,2,7,306,1,5,1,2,1,...] | 1728 a 1777 |
0.56714329040978387299996866221035555 | ||
| 0,54325 89653 42976 70695[Mw 88] | Constante de Bloch-Landau[105] | gamma(1/3) *gamma(5/6) /gamma(1/6) |
A081760 | [0;1,1,5,3,1,1,2,1,1,6,3,1,8,11,2,1,1,27,4,...] | 1929 | 0.54325896534297670695272829530061323 | ||||
| 0,34053 73295 50999 14282[Mw 89] | Constante de Pólya Random Walk[106] | 
|
|
1-16*Sqrt[2/3]*Pi^3 /((Gamma[1/24] *Gamma[5/24] *Gamma[7/24] *Gamma[11/24]) |
A086230 | [0;2,1,14,1,3,8,1,5,2,7,1,12,1,5,59,1,1,1,3,...] | 0.34053732955099914282627318443290289 | |||
| 0,35323 63718 54995 98454[Mw 90] | Constante de Hafner-Sarnak-McCurley (1)[107] | prod[k=1 to ∞] {1-(1-prod[j=1 to n] {1-prime(k)^-j})^2} | A085849 | [0;2,1,4,1,10,1,8,1,4,1,2,1,2,1,2,6,1,1,1,3,...] | 1993 | 0.35323637185499598454351655043268201 | ||||
| 0,74759 79202 53411 43517[Mw 91] | Constante Parking de Rényi[108] | 
|
[e^(-2*Gamma)] * Int{n,0,∞}[ e^(- 2*Gamma(0,n)) /n^2] | A050996 | [0;1,2,1,25,3,1,2,1,1,12,1,2,1,1,3,1,2,1,43,...] | 1958 | 0.74759792025341143517873094383017817 | |||
| 0,60792 71018 54026 62866[Mw 92] | Constante de Hafner-Sarnak-McCurley (2)[109] | Prod{n=1 to ∞} (1-1/prime(n)^2) |
T | A059956 | [0;1,1,1,1,4,2,4,7,1,4,2,3,4,10,1,2,1,1,1,...] | 0.60792710185402662866327677925836583 | ||||
| 0,12345 67891 01112 13141[Mw 93] | Constante de Champernowne[110] | 
|
T | A033307 | [0;8,9,1,149083,1,1,1,4,1,1,1,3,4,1,1,1,15,...] | 1933 | 0.12345678910111213141516171819202123 | |||
| 0,76422 36535 89220 66299[Mw 94] | Constante de Landau-Ramanujan[111] | T ? | A064533 | [0;1,3,4,6,1,15,1,2,2,3,1,23,3,1,1,3,1,1,6,4,...] | 1908 | 0.76422365358922066299069873125009232 | ||||
| 1,58496 25007 21156 18145[Mw 95] | Dimensión de Hausdorf del triángulo de Sierpinski[112] | 
|
( Sum[n=0 to ∞] {1/(2^(2n+1)(2n+1))})/ ( Sum[n=0 to ∞] {1/(3^(2n+1)(2n+1))}) |
T | A020857 | [1;1,1,2,2,3,1,5,2,23,2,2,1,1,55,1,4,3,1,1,...] | 1.58496250072115618145373894394781651 | |||
| 0,11000 10000 00000 00000 0001 [Mw 96] | Número de Liouville[113] | Sum[n=1 to ∞] {10^(-n!)} |
T | A012245 | [1;9,1,999,10,9999999999999,1,9,999,1,9] | 0.11000100000000000000000100... | ||||
| 0,46364 76090 00806 11621 | Serie de Machin-Gregory[114] | 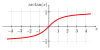
|
Sum[n=0 to ∞] {(-1)^n (1/2) ^(2n+1)/(2n+1)} |
I | A073000 | [0;2,6,2,1,1,1,6,1,2,1,1,2,10,1,2,1,2,1,1,1,...] | 0.46364760900080611621425623146121440 | |||
| 1,27323 95447 35162 68615 | Serie de Ramanujan-Forsyth[115] | Sum[n=0 to ∞] {[(2n-3)!! /(2n)!!]^2} |
I | A088538 | [1;3,1,1,1,15,2,72,1,9,1,17,1,2,1,5,1,1,10,...] | 1.27323954473516268615107010698011489 | ||||
| 15,15426 22414 79264 1897[Mw 97] | Constante exponencial reiterado[116] | 
|
Sum[n=0 to ∞] {(e^n)/n!} |
A073226 | [15;6,2,13,1,3,6,2,1,1,5,1,1,1,9,4,1,1,1,6,7,...] | 15.1542622414792641897604302726299119 | ||||
| 36,46215 96072 07911 77099 | Pi elevado a pi[117] | pi^pi | A073233 | [36;2,6,9,2,1,2,5,1,1,6,2,1,291,1,38,50,1,2,...] | 36.4621596072079117709908260226921236 | |||||
| 0,53964 54911 90413 18711 | Constante de Ioachimescu[118] | γ +N [sum[n=1 to ∞] {((-1)^(2n) gamma_n) /(2^n n!)}] |
2- A059750 |
[0;1,1,5,1,4,6,1,1,2,6,1,1,2,1,1,1,37,3,2,1,...] | 0.53964549119041318711050084748470198 | |||||
| 2,58498 17595 79253 21706[Mw 98] | Constante de Sierpiński[119] | 
|
|
-Pi Log[Pi]+2 Pi EulerGamma +4 Pi Log [Gamma[3/4]] |
A062089 | [2;1,1,2,2,3,1,3,1,9,2,8,4,1,13,3,1,15,18,1,...] | 1907 | 2.58498175957925321706589358738317116 | ||
| 1,83928 67552 14161 13255 | Constante Tribonacci[120] | 
|
(1/3)*(1+(19+3 *sqrt(33))^(1/3) +(19-3 *sqrt(33))^(1/3)) |
A | A058265 | [1;1,5,4,2,305,1,8,2,1,4,6,14,3,1,13,5,1,7,...] | 1.83928675521416113255185256465328660 | |||
| 0,69220 06275 55346 35386[Mw 99] | Valor mínimo de la función ƒ(x) = xx [121] |
|
e^(-1/e) | A072364 | [0;1,2,4,55,27,1,1,16,9,3,2,8,3,2,1,1,4,1,9,...] | 0.69220062755534635386542199718278976 | ||||
| 0,70710 67811 86547 52440 +0,70710 67811 86547 52440 i |
Raíz cuadrada de i [122] | 
|
(1+i)/(sqrt 2) | C A | A010503 A010503 |
[0;1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,..] = [0;1,2,...] [0;1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,..] i = [0;1,2,...] i |
0.70710678118654752440084436210484903 + 0.70710678118654752440084436210484 i | |||
| 1,15636 26843 32269 71685[Mw 100] | Constante de recurrencia cúbica[123] | prod[n=1 to ∞] {n ^(1/3)^n} |
A123852 | [1;6,2,1,1,8,13,1,3,2,2,6,2,1,2,1,1,1,10,33,...] | 1.15636268433226971685337032288736935 | |||||
| 1,66168 79496 33594 12129[Mw 101] | Recurrencia cuadrática de Somos[124] | prod[n=1 to ∞] {n ^(1/2)^n} |
T ? | A065481 | [1;1,1,1,21,1,1,1,6,4,2,1,1,2,1,3,1,13,13,...] | 1.66168794963359412129581892274995074 | ||||
| 0,95531 66181 24509 27816 | Ángulo mágico[125] | 
|
arctan(sqrt(2)) | T | A195696 | [0;1,21,2,1,1,1,2,1,2,2,4,1,2,9,1,2,1,1,1,3,...] | 0.95531661812450927816385710251575775 | |||
| 0,59634 73623 23194 07434[Mw 102] | Constante de Euler-Gompertz[126] | N[int[0 to ∞] {(e^-n)/(1+n)}] |
I | A073003 | [0;1,1,2,10,1,1,4,2,2,13,2,4,1,32,4,8,1,1,1,...] | 0.59634736232319407434107849936927937 | ||||
| 0,69777 46579 64007 98200[Mw 103] | Constante de fracción continua, función de Bessel[127] | (Sum {n=0 to ∞} n/(n!n!)) / (Sum {n=0 to ∞} 1/(n!n!)) |
I | A052119 | [0;1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,...] = [0;p+1], p∈ℕ |
0.69777465796400798200679059255175260 | ||||
| 0,36651 29205 81664 32701 | Mediana distribución de Gumbel[128] | 
|
-ln(ln(2)) | A074785 | [0;2,1,2,1,2,6,1,6,6,2,2,2,1,12,1,8,1,1,3,1,...] | 0.36816512920566432701243915823266947 | ||||
| 0,64624 54398 94813 30426[Mw 104] | Constante de Masser-Gramain[129] |
|
Pi/4*(2*Gamma + 2*Log[2] + 3*Log[Pi] - 4 Log[Gamma[1/4]]) |
A086057 | [0;1,1,1,4,1,3,2,3,9,1,33,1,4,3,3,5,3,1,3,4,...] | 0.64624543989481330426647339684579279 | ||||
| 0.69034 71261 14964 31946 | Límite superior exponencial iterado[130] | 
|
2^-3^-4^-5^-6^ -7^-8^-9^-10^ -11^-12^-13 … |
A242760 | [0;1,2,4,2,1,3,1,2,2,1,4,1,2,4,3,1,1,10,1,3,2,...] | 0.69034712611496431946732843846418942 | ||||
| 0,65836 55992 | Límite inferior exponencial iterado[131] | 2^-3^-4^-5^-6^ -7^-8^-9^-10^ -11^-12 … |
[0;1,1,1,12,1,2,1,1,4,3,1,1,2,1,2,1,51,2,2,1,...] | 0.6583655992... | ||||||
| 2,71828 18284 59045 23536[Mw 105] | Número e, constante de Euler[132] | 
|
Sum[n=0 to ∞] {1/n!} |
T | A001113 | [2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,...] = [2;1,2p,1], p∈ℕ |
1618 | 2.71828182845904523536028747135266250 | ||
| 2,74723 82749 32304 33305 | Raíces anidadas de Ramanujan R5 [133] | (2+sqrt(5) +sqrt(15 -6 sqrt(5)))/2 |
A | [2;1,2,1,21,1,7,2,1,1,2,1,2,1,17,4,4,1,1,4,2,...] | 2.74723827493230433305746518613420282 | |||||
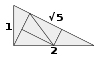
| 2,23606 79774 99789 69640[Mw 106] | Raíz cuadrada de cinco Suma de Gauss[134] |
|
Sum[k=0 to 4] {e^(2k^2 pi i/5)} |
A | A002163 | [2;4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,...] = [2;4,...] |
2.23606797749978969640917366873127624 | |||
| 1,09864 19643 94156 48573[Mw 107] | Constante París | con y | A105415 | [1;10,7,3,1,3,1,5,1,4,2,7,1,2,3,22,1,2,5,2,1,...] | 1.09864196439415648573466891734359621 | |||||
| 0,11494 20448 53296 20070[Mw 108] | Constante de Kepler–Bouwkamp[135] | 
|
prod[n=3 to ∞] {cos(pi/n)} |
A085365 | [0;8,1,2,2,1,272,2,1,41,6,1,3,1,1,26,4,1,1,...] | 0.11494204485329620070104015746959874 | ||||
| 1,28242 71291 00622 63687[Mw 109] | Constante de Glaisher–Kinkelin[136] | e^(1/2-zeta´{-1}) | T ? | A074962 | [1;3,1,1,5,1,1,1,3,12,4,1,271,1,1,2,7,1,35,...] | 1878 | 1.28242712910062263687534256886979172 | |||
| 3,62560 99082 21908 31193[Mw 110] | Gamma(1/4)[137] | 
|
4(1/4)! | T | A068466 | [3;1,1,1,2,25,4,9,1,1,8,4,1,6,1,1,19,1,1,4,1,...] | 1729 | 3.62560990822190831193068515586767200 | ||
| 1,78107 24179 90197 98523[Mw 111] | Exp.gamma por función G-Barnes[138] |
|
Prod[n=1 to ∞] {e^(1/n)}/{1 + 1/n} |
A073004 | [1;1,3,1,1,3,5,4,1,1,2,2,1,7,9,1,16,1,1,1,2,...] | 1900 | 1.78107241799019798523650410310717954 | |||
| 0,18785 96424 62067 12024[Mw 112] | MRB Constant, Marvin Ray Burns[139][140][141] | 
|
Sum[n=1 to ∞] {(-1)^n (n^(1/n)-1)} |
A037077 | [0;5,3,10,1,1,4,1,1,1,1,9,1,1,12,2,17,2,2,1,...] | 1999 | 0.18785964246206712024851793405427323 | |||
| 1,01494 16064 09653 62502[Mw 113] | Constante de Gieseking[142] |
|
sqrt(3)*3/4 *(1 -Sum[n=0 to ∞] {1/((3n+2)^2)} +Sum[n=1 to ∞] {1/((3n+1)^2)}) |
A143298 | [1;66,1,12,1,2,1,4,2,1,3,3,1,4,1,56,2,2,11,...] | 1912 | 1.01494160640965362502120255427452028 | |||
| 2,62205 75542 92119 81046[Mw 114] | Constante Lemniscata[143] | 
|
4 sqrt(2/pi) ((1/4)!)^2 |
T | A062539 | [2;1,1,1,1,1,4,1,2,5,1,1,1,14,9,2,6,2,9,4,1,...] | 1798 | 2.62205755429211981046483958989111941 | ||
| 0,83462 68416 74073 18628[Mw 115] | Constante de Gauss[144] | (4 sqrt(2) ((1/4)!)^2) /pi^(3/2) |
T | A014549 | [0;1,5,21,3,4,14,1,1,1,1,1,3,1,15,1,3,7,1,...] | 1799 | 0.83462684167407318628142973279904680 | |||
| 0,00787 49969 97812 3844[Mw 116] | Constante de Chaitin[145] | Ver también: Problema de la parada |
T | A100264 | [0; 126, 1, 62, 5, 5, 3, 3, 21, 1, 4, 1] | 1975 | 0.0078749969978123844 | |||
| 2,80777 02420 28519 36522[Mw 117] | Constante Fransén–Robinson[146] | N[int[0 to ∞] {1/Gamma(x)}] |
A058655 | [2;1,4,4,1,18,5,1,3,4,1,5,3,6,1,1,1,5,1,1,1...] | 1978 | 2.80777024202851936522150118655777293 | ||||
| 1,01734 30619 84449 13971[Mw 118] | Zeta(6)[147] | 
|
|
Prod[n=1 to ∞] {1/(1 -prime(n)^-6)} |
T | A013664 | [1;57,1,1,1,15,1,6,3,61,1,5,3,1,6,1,3,3,6,1,...] | 1.01734306198444913971451792979092052 | ||
| 1,64872 12707 00128 14684[Ow 6] | Raíz cuadrada del número e[148] | sum[n=0 to ∞] {1/(2^n n!)} |
T | A019774 | [1;1,1,1,5,1,1,9,1,1,13,1,1,17,1,1,21,1,1,...] = [1;1,1,1,4p+1], p∈ℕ |
1.64872127070012814684865078781416357 | ||||
| Número imaginario[149] | 
|
sqrt(-1) | CI | 1501 à 1576 |
||||||
| 4,81047 73809 65351 65547 | Constante de John[150] | e^(π/2) | T | A042972 | [4;1,4,3,1,1,1,1,1,1,1,1,7,1,20,1,3,6,10,3,...] | 4.81047738096535165547303566670383313 | ||||
| 0.49801 56681 18356 04271 0.15494 98283 01810 68512 i |
Factorial de i[151] | Gamma(1+i) | C | A212877 A212878 |
[0;6,2,4,1,8,1,46,2,2,3,5,1,10,7,5,1,7,2,...] - [0;2,125,2,18,1,2,1,1,19,1,1,1,2,3,34,...] i |
0.49801566811835604271369111746219809 - 0.15494982830181068512495513048388 i | ||||
| 0,43828 29367 27032 11162 0,36059 24718 71385 485 i[Mw 120] |
Tetración infinita de i [152] | i^i^i^... | C | A077589 A077590 |
[0;2,3,1,1,4,2,2,1,10,2,1,3,1,8,2,1,2,1, ...] + [0;2,1,3,2,2,3,1,5,5,1,2,1,10,10,6,1,1...] i |
0.43828293672703211162697516355126482 + 0.36059247187138548595294052690600 i | ||||
| 0,56755 51633 06957 82538 | Módulo de la Tetración infinita de i[153] |
Mod(i^i^i^...) | A212479 | [0;1,1,3,4,1,58,12,1,51,1,4,12,1,1,2,2,3,...] | 0.56755516330695782538461314419245334 | |||||
| 0,26149 72128 47642 78375[Mw 121] | Constante de Meissel-Mertens[154] | 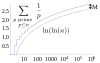
|
gamma+ Sum[n=1 to ∞] {ln(1-1/prime(n)) +1/prime(n)} |
A077761 | [0;3,1,4,1,2,5,2,1,1,1,1,13,4,2,4,2,1,33,296,...] | 1866 y 1873 |
0.26149721284764278375542683860869585 | |||
| 1,92878 00...[Mw 122] | Constante de Wright[155] | = primos: =3, =13, =16381, | A086238 | [1; 1, 13, 24, 2, 1, 1, 3, 1, 1, 3] | 1.9287800.. | |||||
| 0,37395 58136 19202 28805[Mw 123] | Constante de Artin[156] | Prod[n=1 to ∞] {1-1/(prime(n) (prime(n)-1))} |
A005596 | [0;2,1,2,14,1,1,2,3,5,1,3,1,5,1,1,2,3,5,46,...] | 1999 | 0.37395581361920228805472805434641641 | ||||
| 4,66920 16091 02990 67185[Mw 124] | Constante δ de Feigenbaum δ [157] | 
|
|
A006890 | [4;1,2,43,2,163,2,3,1,1,2,5,1,2,3,80,2,5,...] | 1975 | 4.66920160910299067185320382046620161 | |||
| 2,50290 78750 95892 82228[Mw 125] | Constante α de Feigenbaum[158] | 
|
A006891 | [2;1,1,85,2,8,1,10,16,3,8,9,2,1,40,1,2,3,...] | 1979 | 2.50290787509589282228390287321821578 | ||||
| 5,97798 68121 78349 12266[Mw 126] | Constante hexagonal Madelung 2 [159] | Pi Log[3]Sqrt[3] | A086055 | [5;1,44,2,2,1,15,1,1,12,1,65,11,1,3,1,1,...] | 5.97798681217834912266905331933922774 | |||||
| 0,96894 61462 59369 38048 | Constante Beta(3)[160] | Sum[n=1 to ∞] {(-1)^(n+1) /(-1+2n)^3} |
T | A153071 | [0;1,31,4,1,18,21,1,1,2,1,2,1,3,6,3,28,1,...] | 0.96894614625936938048363484584691860 | ||||
| 1,90216 05831 04[Mw 127] | Constante de Brun 2 = Σ inverso primos gemelos[161] |

|
N[prod[n=2 to 0,870∞] [1-1/(prime(n) -1)^2]] |
A065421 | [1; 1, 9, 4, 1, 1, 8, 3, 4, 4, 2, 2] | 1919 | 1.902160583104 | |||
| 0,87058 83799 75[Mw 128] | Constante de Brun 4 = Σ inverso primos gemelos[162] |
A213007 | [0; 1, 6, 1, 2, 1, 2, 956, 3, 1, 1] | 1919 | 0.87058837997 | |||||
| 22,45915 77183 61045 47342 | pi^e[163] | pi^e | A059850 | [22;2,5,1,1,1,1,1,3,2,1,1,3,9,15,25,1,1,5,...] | 22.4591577183610454734271522045437350 | |||||
| 3,14159 26535 89793 23846[Mw 129] | Número π, constante de Arquímedes[164] ·[165] | Sum[n=0 to ∞] {(-1)^n 4/(2n+1)} |
T | A000796 | [3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,2,2,...] | -250 ~ | 3.14159265358979323846264338327950288 | |||
| 0,28878 80950 86602 42127[Mw 130] | Flajolet and Richmond[166] | prod[n=1 to ∞] {1-1/2^n} |
A048651 | [0;3,2,6,4,1,2,1,9,2,1,2,3,2,3,5,1,2,1,1,6,1,...] | 1992 | 0.28878809508660242127889972192923078 | ||||
| 0,06598 80358 45312 53707[Mw 131] | Límite inferior de Tetración[167] | 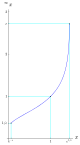
|
1/(e^e) | A073230 | [0;15,6,2,13,1,3,6,2,1,1,5,1,1,1,9,4,1,1,1,...] | 0.06598803584531253707679018759684642 | ||||
| 0,31830 98861 83790 67153[Mw 132] | Inverso de Pi, Ramanujan[168] | 2 sqrt(2)/9801 *Sum[n=0 to ∞] {((4n)!/n!^4)*(1103+ 26390n)/396^(4n)} |
T | A049541 | [0;3,7,15,292,1,1,1,2,1,3,1,14,2,1,1,2,2,2,...] | 0.31830988618379067153776752674502872 | ||||
| 0,63661 97723 67581 34307[Mw 133][Ow 7] | Constante de Buffon[169] |  Aguja interseca línea Aguja interseca línea
|
2/Pi | T | A060294 | [0;1,1,1,3,31,1,145,1,4,2,8,1,6,1,2,3,1,4,...] | 1540 a 1603 |
0.63661977236758134307553505349005745 | ||
| 0,47494 93799 87920 65033[Mw 134] | Constante de Weierstrass[170] | (E^(Pi/8) Sqrt[Pi]) /(4 2^(3/4) (1/4)!^2) |
A094692 | [0;2,9,2,11,1,6,1,4,6,3,19,9,217,1,2,4,8,6...] | 1872 ? | 0.47494937998792065033250463632798297 | ||||
| 0,57721 56649 01532 86060[Mw 135] | Constante de Euler-Mascheroni[171] | 
|
sum[n=1 to ∞] |sum[k=0 to ∞] {((-1)^k)/(2^n+k)} |
A001620 | [0;1,1,2,1,2,1,4,3,13,5,1,1,8,1,2,4,1,1,40,1,...] | 1735 | 0.57721566490153286060651209008240243 | |||
| 1,70521 11401 05367 76428[Mw 136] | Constante de Niven[172] | 1+ Sum[n=2 to ∞] {1-(1/Zeta(n))} |
A033150 | [1;1,2,2,1,1,4,1,1,3,4,4,8,4,1,1,2,1,1,11,1,...] | 1969 | 1.70521114010536776428855145343450816 | ||||
| 0,60459 97880 78072 61686[Mw 137] | Relación entre el área de un triángulo equilátero y su círculo inscrito. | 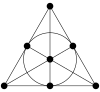
|
|
Sum[1/(n Binomial[2 n, n]) , {n, 1, ∞}] |
T | A073010 | [0;1,1,1,1,8,10,2,2,3,3,1,9,2,5,4,1,27,27,6,6,...] | 0.60459978807807261686469275254738524 | ||
| 3,24697 96037 17467 06105[Mw 138] | Constante Silver de Tutte–Beraha[173] | 2+2 cos(2Pi/7) | A | A116425 | [3;4,20,2,3,1,6,10,5,2,2,1,2,2,1,18,1,1,3,2,...] | 3.24697960371746706105000976800847962 | ||||
| 0,69314 71805 59945 30941[Mw 139] | Logaritmo natural de 2 | 
|
Sum[n=1 to ∞] {(-1)^(n+1)/n} |
T | A002162 | [0;1,2,3,1,6,3,1,1,2,1,1,1,1,3,10,1,1,1,2,1,1,...] | 1550 a 1617 |
0.69314718055994530941723212145817657 | ||
| 0,66016 18158 46869 57392[Mw 140] | Constante de los primos gemelos[174] | prod[p=3 to ∞] {p(p-2)/(p-1)^2 |
A005597 | [0;1,1,1,16,2,2,2,2,1,18,2,2,11,1,1,2,4,1,...] | 1922 | 0.66016181584686957392781211001455577 | ||||
| 0,66274 34193 49181 58097[Mw 141] | Constante límite de Laplace[175] | 
|
(x e^sqrt(x^2+1)) /(sqrt(x^2+1)+1) = 1 |
A033259 | [0;1,1,1,27,1,1,1,8,2,154,2,4,1,5,1,1,2,1601,...] | 1782 ~ | 0.66274341934918158097474209710925290 | |||
| 0,28016 94990 23869 13303[Mw 142] | Constante de Bernstein[176] | 1/(2 sqrt(pi)) | T | A073001 | [0;3,1,1,3,9,6,3,1,3,14,34,2,1,1,60,2,2,1,1,...] | 1913 | 0.28016949902386913303643649123067200 | |||
| 0,78343 05107 12134 40705[Mw 143] | Sophomore's Dream 1 Johann Bernoulli[177] |

|
Sum[n=1 to ∞] {-(-1)^n /n^n} |
A083648 | [0;1,3,1,1,1,1,1,1,2,4,7,2,1,2,1,1,1,2,1,14,...] | 1697 | 0.78343051071213440705926438652697546 | |||
| 1,29128 59970 62663 54040[Mw 144] | Sophomore's Dream 2 Johann Bernoulli[178] | 
|
Sum[n=1 to ∞] {1/(n^n)} |
A073009 | [1;3,2,3,4,3,1,2,1,1,6,7,2,5,3,1,2,1,8,1,2,4,...] | 1697 | 1.29128599706266354040728259059560054 | |||
| 0,82246 70334 24113 21823[Mw 145] | Constante Nielsen-Ramanujan[179] | Sum[n=1 to ∞] {((-1)^(n+1))/n^2} |
T | A072691 | [0;1,4,1,1,1,2,1,1,1,1,3,2,2,4,1,1,1,1,1,1,4...] | 1909 | 0.82246703342411321823620758332301259 | |||
| 0,78539 81633 97448 30961[Mw 146] | Beta(1)[180] | 
|
Sum[n=0 to ∞] {(-1)^n/(2n+1)} |
T | A003881 | [0; 1,3,1,1,1,15,2,72,1,9,1,17,1,2,1,5,...] | 1805 a 1859 |
0.78539816339744830961566084581987572 | ||
| 0,91596 55941 77219 01505[Mw 147] | Constante de Catalan[181][182][183] | Sum[n=0 to ∞] {(-1)^n/(2n+1)^2} |
T ? | A006752 | [0;1,10,1,8,1,88,4,1,1,7,22,1,2,3,26,1,11,...] | 1864 | 0.91596559417721901505460351493238411 | |||
| 1,05946 30943 59295 26456[Ow 8] | Intervalo entre semitonos de la escala musical[184][185] |
|
2^(1/12) | A | A010774 | [1;16,1,4,2,7,1,1,2,2,7,4,1,2,1,60,1,3,1,2,...] | 1.05946309435929526456182529494634170 | |||
| 1,13198 82487 943[Mw 148] | Constante de Viswanath[186] | donde an = Sucesión de Fibonacci | lim_(n->∞) |a_n|^(1/n) |
T ? | A078416 | [1;7,1,1,2,1,3,2,1,2,1,8,1,5,1,1,1,9,1,...] | 1997 | 1.1319882487943 ... | ||
| 1,20205 69031 59594 28539[Mw 149] | Constante de Apéry[187] | 
|
|
Sum[n=1 to ∞] {1/n^3} |
I | A010774 | [1;4,1,18,1,1,1,4,1,9,9,2,1,1,1,2,7,1,1,7,11,...] | 1979 | 1.20205690315959428539973816151144999 | |
| 1,22541 67024 65177 64512[Mw 150] | Gamma(3/4)[188] | (-1+3/4)! | A068465 | [1;4,2,3,2,2,1,1,1,2,1,4,7,1,171,3,2,3,1,1,8,...] | 1.22541670246517764512909830336289053 | |||||
| 1,25992 10498 94873 16476[Mw 151] | Raíz cúbica de dos, constante Delian | 
|
2^(1/3) | A | A002580 | [1;3,1,5,1,1,4,1,1,8,1,14,1,10,2,1,4,12,2,3,...] | 1.25992104989487316476721060727822835 | |||
| 9,86960 44010 89358 61883 | Pi al Cuadrado | 6 Sum[n=1 to ∞] {1/n^2} |
T | A002388 | [9;1,6,1,2,47,1,8,1,1,2,2,1,1,8,3,1,10,5,...] | 9.86960440108935861883449099987615114 | ||||
| 1,41421 35623 73095 04880[Mw 152] | Raíz cuadrada de 2, constante de Pitágoras[189] | 
|
prod[n=1 to ∞] {1+(-1)^(n+1) /(2n-1)} |
A | A002193 | [1;2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,...] = [1;2...] |
< -800 | 1.41421356237309504880168872420969808 | ||
| 262 53741 26407 68743 ,99999 99999 99250 073[Mw 153] |
Constante de Hermite-Ramanujan[190] | e^(π sqrt(163)) | T | A060295 | [262537412640768743;1,1333462407511,1,8,1,1,5,...] | 1859 | 262537412640768743.999999999999250073 | |||
| 0,76159 41559 55764 88811[Mw 154] | Tangente hiperbólica de 1[191] | 
|
(e-1/e)/(e+1/e) | T | A073744 | [0;1,3,5,7,9,11,13,15,17,19,21,23,25,27,...] = [0;2p+1], p∈ℕ |
0.76159415595576488811945828260479359 | |||
| 0,36787 94411 71442 32159[Mw 155] | Inverso del Número e[192] | sum[n=2 to ∞] {(-1)^n/n!} |
T | A068985 | [0;2,1,1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,...] = [0;2,1,1,2p,1], p∈ℕ |
1618 | 0.36787944117144232159552377016146086 | |||
| 1,53960 07178 39002 03869[Mw 156] | Constante Square Ice de Lieb[193] | (4/3)^(3/2) | A | A118273 | [1;1,1,5,1,4,2,1,6,1,6,1,2,4,1,5,1,1,2,...] | 1967 | 1.53960071783900203869106341467188655 | |||
| 1,23370 05501 36169 82735[Mw 157] | Constante de Favard[194] | sum[n=1 to ∞] {1/((2n-1)^2)} |
T | A111003 | [1;4,3,1,1,2,2,5,1,1,1,1,2,1,2,1,10,4,3,1,1,...] | 1902 a 1965 |
1.23370055013616982735431137498451889 | |||
| 7,38905 60989 30650 22723 | Constante cónica de Schwarzschild[195] | 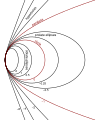
|
Sum[n=0 to ∞] {2^n/n!} |
T | A072334 | [7;2,1,1,3,18,5,1,1,6,30,8,1,1,9,42,11,1,...] = [7,2,1,1,n,4*n+6,n+2], n = 3, 6, 9, etc. |
7.38905609893065022723042746057500781 | |||
| 0,20787 95763 50761 90854[Mw 158] | i^i[196] | e^(-pi/2) | T | A049006 | [0;4,1,4,3,1,1,1,1,1,1,1,1,7,1,20,1,3,6,10,...] | 1746 | 0.20787957635076190854695561983497877 | |||
| 1,44466 78610 09766 13365[Mw 159] | Número de Steiner[197] |  |
|
e^(1/e) | A073229 | [1;2,4,55,27,1,1,16,9,3,2,8,3,2,1,1,4,1,9,...] | 1796 a 1863 |
1.44466786100976613365833910859643022 | ||
| 4,53236 01418 27193 80962 | Constante de van der Pauw | π/ln(2) | A163973 | [4;1,1,7,4,2,3,3,1,4,1,1,4,7,2,3,3,12,2,1,...] | 4.53236014182719380962768294571666681 | |||||
| 1,57079 63267 94896 61923[Mw 160] | Constante de Favard K1 Producto de Wallis[198] |

|
Prod[n=1 to ∞] {(4n^2)/(4n^2-1)} |
A019669 | [1;1,1,3,31,1,145,1,4,2,8,1,6,1,2,3,1,4,1,5,1...] | 1655 | 1.57079632679489661923132169163975144 | |||
| 3,27582 29187 21811 15978[Mw 161] | Constante de Khinchin-Lévy[199] ·[200] | e^(\pi^2/(12 ln(2)) | A086702 | [3;3,1,1,1,2,29,1,130,1,12,3,8,2,4,1,3,55,...] | 1936 | 3.27582291872181115978768188245384386 | ||||
| 1,61803 39887 49894 84820[Mw 162] | Phi, Número áureo[201] ·[202] | 
|
(1+5^(1/2))/2 | A | A001622 | [0;1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,...] = [0;1,...] |
-300 ~ | 1.61803398874989484820458683436563811 | ||
| 1,64493 40668 48226 43647[Mw 163] | Función Zeta (2) de Riemann | Sum[n=1 to ∞] {1/n^2} |
T | A013661 | [1;1,1,1,4,2,4,7,1,4,2,3,4,10 1,2,1,1,1,15,...] | 1826 a 1866 |
1.64493406684822643647241516664602519 | |||
| 1,73205 08075 68877 29352[Mw 164] | Constante de Theodorus[203] | 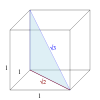
|
(3(3(3(3(3(3(3) ^1/3)^1/3)^1/3) ^1/3)^1/3)^1/3) ^1/3 ... |
A | A002194 | [1;1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,...] = [1;1,2,...] |
-465 a -398 |
1.73205080756887729352744634150587237 | ||
| 1,75793 27566 18004 53270[Mw 165] | Número de Kasner[204] | A072449 | [1;1,3,7,1,1,1,2,3,1,4,1,1,2,1,2,20,1,2,2,...] | 1878 a 1955 |
1.75793275661800453270881963821813852 | |||||
| 2,29558 71493 92638 07403[Mw 166] | Constante universal parabólica[205] | 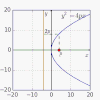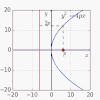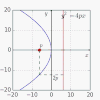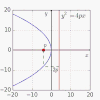
|
ln(1+sqrt 2)+sqrt 2 | T | A103710 | [2;3,2,1,1,1,1,3,3,1,1,4,2,3,2,7,1,6,1,8,7,2,1,...] | 2.29558714939263807403429804918949038 | |||
| 3,30277 56377 31994 64655[Mw 167] | Número de bronce[206] | (3+sqrt 13)/2 | A | A098316 | [3;3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,...] = [3;3,...] |
3.30277563773199464655961063373524797 | ||||
| 2,37313 82208 31250 90564 | Constante de Lévy 2 [207] | Pi^(2)/(6*ln(2)) | T | A174606 | [2;2,1,2,8,57,9,32,1,1,2,1,2,1,2,1,2,1,3,2,...] | 1936 | 2.37313822083125090564344595189447424 | |||
| 2,50662 82746 31000 50241 | Raíz cuadrada de 2 pi | 
|
Fórmula de Stirling | sqrt (2*pi) | T | A019727 | [2;1,1,37,4,1,1,1,1,9,1,1,2,8,6,1,2,2,1,3,...] | 1692 a 1770 |
2.50662827463100050241576528481104525 | |
| 2,66514 41426 90225 18865[Mw 168] | Constante de Gelfond-Schneider[208] | 2^sqrt{2} | T | A007507 | [2;1,1,1,72,3,4,1,3,2,1,1,1,14,1,2,1,1,3,1,...] | 1934 | 2.66514414269022518865029724987313985 | |||
| 2,68545 20010 65306 44530[Mw 169] | Constante de Khinchin[209] | 
|
... donde ak son elementos de la fracción continua [a0; a1, a2, a3, ...] |
prod[n=1 to ∞] {(1+1/(n(n+2))) ^((ln(n)/ln(2))} |
T | A002210 | [2;1,2,5,1,1,2,1,1,3,10,2,1,3,2,24,1,3,2,...] | 1934 | 2.68545200106530644530971483548179569 | |
| 3,35988 56662 43177 55317[Mw 170] | Constante de Prévost, sum. inversos de Fibonacci[210] | I | A079586 | [3;2,1,3,1,1,13,2,3,3,2,1,1,6,3,2,4,362,...] | 1977 | 3.35988566624317755317201130291892717 | ||||
| 1,32471 79572 44746 02596[Mw 171] | Número plástico[211] | 
|
A | A060006 | [1;3,12,1,1,3,2,3,2,4,2,141,80,2,5,1,2,8,...] | 1929 | 1.32471795724474602596090885447809734 | |||
| 4,13273 13541 22492 93846 | Raíz de 2 e pi | sqrt(2e pi) | A019633 | [4;7,1,1,6,1,5,1,1,1,8,3,1,2,2,15,2,1,1,2,4,...] | 4.13273135412249293846939188429985264 | |||||
| 23,14069 26327 79269 00572 [Mw 172] | Constante de Gelfond[212] | Sum[n=0 to ∞] {(pi^n)/n!} |
T | A039661 | [23;7,9,3,1,1,591,2,9,1,2,34,1,16,1,30,1,...] | 1906 a 1968 |
23.1406926327792690057290863679485474 |
Tabla de constantes matemáticas[editar]
Abreviaciones usadas:
- R - Número racional
- I - Número irracional algebraico
- T - número irracional trascendental
- ? - desconocido
| 0 | 0 | cero | R | - | - |
| 1 | 1 | uno | R | - | - |
| 2 | 2 | dos | R | - | - |
| 3,14159 26535 89793 23846 26433 83279 50288 41971 | Pi, constante de Arquímedes o número de Ludolph | T | 10.000.000.000.050[213] | 22/10/2011 | |
| 2,71828 18284 59045 23536 02874 71352 66249 77572 | Constante de Napier, base del logaritmo natural | T | 1.000.000.000.000[214][215] | 2010 | |
| 1,41421 35623 73095 04880 16887 24209 69807 85696 | Raíz cuadrada de dos, constante de Pitágoras. | I | 1.000.000.000.000[215] | 2010 | |
| 1,73205 08075 68877 29352 74463 41505 87236 69428 | Raíz cuadrada de tres | I | 10.000.000 | ||
| 2,23606 79774 99789 69640 91736 68731 27623 54406 | Raíz cuadrada de cinco | I | 10.000.000[216] | 20/12/1999 | |
| 1,61803 39887 49894 84820 45868 34365 63811 77203 | Número áureo, simbolizado tanto como φ como por τ. | I | 1.000.000.000.000[215] | 2010 | |
| 0,57721 56649 01532 86060 65120 90082 40243 10421 | Constante de Euler-Mascheroni | ? | 29.844.489.545[215] | 2009 | |
| -2,50290 78750 95892 82228 39028 73218 21578 63812 | Constante α de Feigenbaum | 1018[217] | 1999 | ||
| 4,66920 16091 02990 67185 32038 20466 20161 72581 | Constante δ de Feigenbaum | 1018[217] | 1999 | ||
| 0,37395 58136 19202 28805 47280 54346 41641 51116 | Constante de Artin | 1000[215] | 1999 | ||
| 0,66016 18158 46869 57392 78121 10014 55577 84326 | Constante de los primos gemelos | 5.020[215] | 2001 | ||
| 1,90216 0582 | Constante de Brun para los primos gemelos | 9[215] | 1999 / 2002 |
Libros[editar]
- Finch, Steven (2003). Mathematical constants. Cambridge University Press. ISBN 978-0-521-81805-6.
- Daniel Zwillinger (2012). Standard Mathematical Tables and Formulae. Imperial College Press. ISBN 978-1-4398-3548-7.
- Eric W. Weisstein (2003). CRC Concise Encyclopedia of Mathematics. Chapman & Hall/CRC. ISBN 1-58488-347-2.
- Lloyd Kilford (2008). Modular Forms, a Classical and Computational Introduction. Imperial College Press. ISBN 978-1-84816-213-6.
Referencias[editar]
- ↑ Koshy (2017). Fibonacci and Lucas Numbers with Applications (en inglés) (2 edición). John Wiley & Sons. ISBN 9781118742174. Consultado el 14 de agosto de 2018. }}
- ↑ Thomas Kerigan (1838). Mills and Son, ed. The Complete Mathematical and General Navigation Tables, Vol. 2. p. 669.
- ↑ Thomas Hales, Samuel Ferguson (2010). Springer, Jeffrey C. Lagarias, ed. The Kepler Conjecture: The Hales-Ferguson Proof. ISBN 978-1-4614-1128-4.
- ↑ Fernando Blasco (2014). Investigación y Ciencia, ed. Apilando naranjas.
- ↑ Robert Baillie (2013). arxiv, ed. Summing The Curious Series of Kempner and Irwin. p. 9.
- ↑ Leonhard Euler (1749). Consideratio quarumdam serierum, quae singularibus proprietatibus sunt praeditae. p. 108.
- ↑ RICHARD J. MATHAR (2010). Arxiv.org, ed. NUMERICAL EVALUATION OF THE OSCILLATORY INTEGRAL BETWEEN 1 AND INFINITY.
- ↑ Marvin Ray Burns. RECORD CALCULATIONS OF THE MKB CONSTANT.
- ↑ Steven Finch (2014). Harvard.edu, ed. Errata and Addenda to Mathematical Constants. p. 63.
- ↑ István Mezö (2011). University of Debrecen, Hungary, ed. On the integral of the fourth Jacobi theta function.
- ↑ University of Nebraska–Lincoln, ed. (2010). Volume and Surface area of the Spherical Tetrahedron (AKA Reuleaux tetrahedron) by geometrical methods.
- ↑ Pei-Chu Hu,Chung-Chun (2008). Hong Kong University, ed. Distribution Theory of Algebraic Numbers. p. 246. ISBN 978-3-11-020536-7.
- ↑ Ángulo áureo.
- ↑ saildart. [GKP,DEK1 Vardi].
- ↑ Robert P. Munafo (2012). Pixel Counting.
- ↑ Dmitrii Kouznetsov (2009). Institute for Laser Science (ILS), (UEC). Japan, ed. SOLUTION OF F(z + 1) = exp F(z) IN COMPLEX z-PLANE.
- ↑ World Heritage Encyclopedia. World eBooK Library, ed. EULER'S INFINITE TETRATION THEOREM.
- ↑ Marius Coman (2013). The Math Encyclopedia of Smarandache type Notions: Vol. I. Number Theory.
- ↑ Eric W. Weisstein (1999). Michigan State University Libraries, ed. Lebesgue Constants (Fourier Series).
- ↑ SERGI ELIZALDE. Arxiv.org, ed. ASYMPTOTIC ENUMERATION OF PERMUTATIONS AVOIDING GENERALIZED PATTERNS.
- ↑ Christoph Lanz. Technischen Universität Wien, ed. k-Automatic Reals.
- ↑ Steven Finch (2014). Harvard.edu, ed. Electrical Capacitance. p. 1.
- ↑ Thomas Ransford. Universite Laval, Quebec (QC), Canada, ed. Computation of Logarithmic Capacity. p. 557.
- ↑ Eric W. Weisstein (2002). Crc Press, ed. CRC Concise Encyclopedia of Mathematics. p. 1212.
- ↑ Clifford A. Pickover (2009). Sterling Publishing, ed. The Math Book. p. 266. ISBN 978-1-4027-5796-9.
- ↑ Steven Finch (2004). Harvard.edu, ed. Unitarism and Infinitarism. p. 1.
- ↑ Mireille Bousquet-Mélou. CNRS, LaBRI, Bordeaux, France, ed. Two-dimensional self-avoiding walks.
- ↑ Hugo Duminil-Copin and Stanislav Smirnov (2011). Universite de Geneve., ed. The connective constant of the honeycomb lattice √ (2 + √ 2).
- ↑ Steven R. Finch (2003). Mathematical Constants. Cambridge University Press. p. 238. ISBN 3-540-67695-3.
- ↑ Nayar. Tata McGraw-Hill Education., ed. The Steel Handbook. p. 953.
- ↑ Steven Finch (2007). Harvard.edu, ed. Series involving Arithmetric Functions. p. 1.
- ↑ Paul B. Slater (2013). University of California, ed. A Hypergeometric Formula .... p. 9.
- ↑ ECKFORD COHEN (1962). University of Tennessee, ed. SOME ASYMPTOTIC FORMULAS IN THE THEORY OF NUMBERS. p. 220.
- ↑ John Srdjan Petrovic (2014). CRC Press, ed. Advanced Calculus: Theory and Practice. p. 65. ISBN 978-1-4665-6563-0.
- ↑ Steven Finch (2014). Harvard.edu, ed. Errata and Addenda to Mathematical Constants. p. 53.
- ↑ FRANZ LEMMERMEYER (2003). arxiv.org, ed. HIGHER DESCENT ON PELL CONICS. I. FROM LEGENDRE TO SELMER. p. 13.
- ↑ Steven Finch (2007). Mathsoft, ed. Moving Sofa Constant.
- ↑ Steven Finch (2014). Harvard.edu, ed. Errata and Addenda to Mathematical Constants.
- ↑ Paul Manneville (2010). Imperial College Press, ed. Instabilities, Chaos and Turbulence. p. 176. ISBN 978-1-84816-392-8.
- ↑ Andrew Granville and K. Soundararajan (1999). Arxiv, ed. The spectrum of multiplicative functions. p. 3.
- ↑ John Horton Conway, Richard K. Guy (1995). Copernicus, ed. The Book of Numbers. p. 242. ISBN 0-387-97993-X.
- ↑ Steven Finch (2007). Harvard University, ed. Continued Fraction Transformation. p. 7.
- ↑ Curtis T. McMullen (1997). Hausdorff dimension and conformal dynamics III: Computation of dimension.
- ↑ J. B. Friedlander, A. Perelli, C. Viola, D.R. Heath-Brown, H.Iwaniec, J. Kaczorowski (2002). Springer, ed. Analytic Number Theory. p. 29. ISBN 978-3-540-36363-7.
- ↑ Simon Plouffe (1998). Université du Québec, ed. The Computation of Certain Numbers Using a Ruler and Compass. p. Vol. 1 (1998), Article 98.1.3.
- ↑ Simon Plouffe. Sum of the product of inverse of primes.
- ↑ Steven R. Finch (1999). Several Constants Arising in Statistical Mechanics. p. 5.
- ↑ Federico Ardila, Richard Stanley. Department of Mathematics, MIT, Cambridge, ed. Several Constants Arising in Statistical Mechanics.
- ↑ Kunihiko Kaneko,Ichiro Tsuda (1997). Complex Systems: Chaos and Beyond. p. 211. ISBN 3-540-67202-8.
- ↑ W.A. Coppel (2000). Springer, ed. Number Theory: An Introduction to Mathematics. p. 480. ISBN 978-0-387-89485-0.
- ↑ Facts On File, Incorporated (1997). Mathematics Frontiers. p. 46. ISBN 978-0-8160-5427-5.
- ↑ Aleksandr Ykovlevich Khinchin (1997). Courier Dover Publications, ed. Continued Fractions. p. 66. ISBN 978-0-486-69630-0.
- ↑ Jean-Pierre Serre (1969-1970). NUMDAM, Séminaire N. Bourbaki., ed. Travaux de Baker. p. 74.
- ↑ Julian Havil (2003). Princeton University Press, ed. Gamma: Exploring Euler's Constant. p. 31. ISBN 9780691141336.
- ↑ Horst Alzer (2002). Journal of Computational and Applied Mathematics, Volume 139, Issue 2. Elsevier. pp. 215-230.
- ↑ P. Habegger (2003). Institut für Mathematik, Universität Basel, Rheinsprung Basel, Switzerland, ed. Multiplicative dependence and isolation I. p. 2.
- ↑ Andrei Vernescu (2007). Gazeta Matemetica seria a revista de cultur matematica anul XXV(CIV)Nr. 1, Constante de tip Euler generalizate. Gazeta Matemetica. p. 14.
- ↑ Steven R. Finch (2003). Cambridge University Press, ed. Mathematical Constants. p. 479. ISBN 3-540-67695-3.
- ↑ Steven Finch (2007). Harvard University, ed. Continued Fraction Transformation III. p. 5.
- ↑ https://oeis.org/A014574
- ↑ University of Florida, Department of Mechanical and Aerospace Engineering (ed.). Evaluation of the complete elliptic integrals by the agm method.
- ↑ Steven Finch (2005). Harvard University, ed. Class Number Theory. p. 8.
- ↑ James Stewart (2010). Brooks/Cole, ed. Single Variable Calculus: Concepts and Contexts. p. 314. ISBN 978-0-495-55972-6.
- ↑ Steven Finch (2005). Harvard University, ed. Class Number Theory. p. 8.
- ↑ Steven R. Finch (2003). Mathematical Constants. Cambridge University Press. p. 421. ISBN 3-540-67695-3.
- ↑ Steven R. Finch (2003). Mathematical Constants. Cambridge University Press. p. 122. ISBN 3-540-67695-3.
- ↑ Benjamin Klopsch (2013). Representation growth and representation zeta functions of groups. Universita del Salento. p. 114. ISSN 1590-0932.
- ↑ Nikos Bagis. Some New Results on Prime Sums (3 The Euler Totient constant). Aristotle University of Thessaloniki. p. 8.
- ↑ Robinson, H.P. (1971-2011). MATHEMATICAL CONSTANTS.. Lawrence Berkeley National Laboratory. p. 40.
- ↑ Annmarie McGonagle (2011). Plattsburgh State University of New York, ed. A New Parameterization for Ford Circles.
- ↑ V. S. Varadarajan (2000). Euler Through Time: A New Look at Old Themes. AMS. ISBN 0-8218-3580-7.
- ↑ Leonhard Euler, Joseph Louis Lagrange (1810). Elements of Algebra, Volumen 1. J. Johnson and Company. p. 333.
- ↑ Eric W. Weisstein (2003). CRC Concise Encyclopedia of Mathematics, Second Edition. CRC Press. p. 151. ISBN 1-58488-347-2.
- ↑ Chebfun Team (2010). Lebesgue functions and Lebesgue constants. MATLAB Central.
- ↑ Simon J. Smith (2005). La Trobe University, Bendigo, Australia, ed. Lebesgue constants in polynomial interpolation.
- ↑ Steven Finch (2005). Harvard University, ed. Minkowski-Siegel Mass Constants. p. 5.
- ↑ J?org Waldvogel (2008). Analytic Continuation of the Theodorus Spiral. p. 16.
- ↑ Steven R. Finch (2003). Cambridge University Press, ed. Mathematical Constants. p. 121. ISBN 978-0-521-81805-6.
- ↑ Chan Wei Ting ... Moire patterns + fractals. p. 16.
- ↑ Sergey Kitaev and Toufik Mansour (2007). «The problem of the pawns». .
- ↑ Francisco J. Aragón Artacho, David H. Baileyy, Jonathan M. Borweinz, Peter B. Borwein (2012). Tools for visualizing real numbers.. p. 33.
- ↑ Jürgen Giesen (1998). UNIVERSITÄT DUISBURG-ESSEN, ed. Papierfalten.
- ↑ Christoph Zurnieden (2008). Descriptions of the Algorithms.
- ↑ James Stuart Tanton (2007). Encyclopedia of Mathematics. p. 458. ISBN 9781438110080.
- ↑ Steven R. Finch (2003). Cambridge University Press, ed. Mathematical Constants. p. 287. ISBN 3-540-67695-3.
- ↑ Richard J.Mathar (2010). «Table of Dirichlet L-series and Prime Zeta». .
- ↑ Leo Murata (1996). On the Average of the Least Primitive Root Modulo p. Meijigakuin University.
- ↑ Angel Chang y Tianrong Zhang. On the Fractal Structure of the Boundary of Dragon Curve.
- ↑ Laith Saadi (2004). Stealth Ciphers. p. 160. ISBN 978-1-41202-409-9.
- ↑ Jonathan Borwein,David Bailey (2008). A K Peters., ed. Mathematics by Experiment Plausible Reasoning in the 21 Century. p. 56. ISBN 978-1-56881-442-1.
- ↑ Michel A. Théra (2002). CMS-AMS, ed. Constructive, Experimental, and Nonlinear Analysis. p. 77. ISBN 0-8218-2167-9---.
- ↑ Dave Benson (2006). Cambridge University Press, ed. Music: A Mathematical Offering. p. 53. ISBN 978-0-521-85387-3.
- ↑ Joe Diestel (1995). Cambridge University Press, ed. Absolutely Summing Operators. p. 29. ISBN 0-521-43168-9.
- ↑ Ilan Vardi (1998). IHES, Bures sur Yvette, ed. Continued Fractions from Euclid till Present.
- ↑ Michael Trott. Wolfram Research, ed. Finding Trott Constants.
- ↑ Johann Georg Soldner (1809). Lindauer, München, ed. Théorie et tables d’une nouvelle fonction transcendante. p. 42.
- ↑ Lorenzo Mascheroni (1792). Petrus Galeatius, Ticini, ed. Adnotationes ad calculum integralem Euleri. p. 17.
- ↑ Yann Bugeaud (2004). Cambridge University Press, ed. Series representations for some mathematical constants. p. 72. ISBN 0-521-82329-3.
- ↑ Horst Alzera, Dimitri Karayannakisb, H.M. Srivastava (2005). Elsevier Inc, ed. Series representations for some mathematical constants. p. 149.
- ↑ H.M. Antia (2000). Birkhäuser Verlag, ed. Numerical Methods for Scientists and Engineers. p. 220. ISBN 3-7643-6715-6.
- ↑ Yann Bugeaud (2012). Cambridge University Press, ed. Distribution Modulo One and Diophantine Approximation. p. 87. ISBN 978-0-521-11169-0.
- ↑ DAVID EUGENE SMITH (1929). McGraw-Hill Book Company. Ihc, ed. A SOURCE BOOK IN MATHEMATICS. p. 250.
- ↑ Steven R. Finch (2005). Harvard University, ed. Quadratic Dirichlet L-Series. p. 12.
- ↑ Albert Gural. Infinite Power Towers.
- ↑ Eric W. Weisstein (2003). CRC Press, ed. CRC Concise Encyclopedia of Mathematics, Second Edition. p. 1688. ISBN 1-58488-347-2.
- ↑ Steven R. Finch (2003). Cambridge University Press, ed. Mathematical Constants. p. 322. ISBN 978-0-521-81805-6.
- ↑ Steven R. Finch (2003). Cambridge University Press, ed. Mathematical Constants. p. 110. ISBN 978-0-521-81805-6.
- ↑ Mathieu Dutour Sikirić,Yoshiaki Itoh (2011). World Scientific Publishing., ed. Random Sequential Packing of Cubes. p. 5. ISBN 978-981-4307-83-3.
- ↑ Holger Hermanns,Roberto Segala (2000). Springer-Verlag, ed. Process Algebra and Probabilistic Methods.. p. 270. ISBN 3-540-67695-3.
- ↑ Michael J. Dinneen,Bakhadyr Khoussainov,Prof. Andre Nies (2012). Springer, ed. Computation, Physics and Beyond. p. 110. ISBN 978-3-642-27653-8.
- ↑ Richard E. Crandall,Carl B. Pomerance (2005). Springer, ed. Prime Numbers: A Computational Perspective. p. 80. ISBN 978-0387-25282-7.
- ↑ Eric W. Weisstein (2002). CRC Press, ed. CRC Concise Encyclopedia of Mathematics, Second Edition. p. 1356. ISBN 1-58488-347-2.
- ↑ Calvin C. Clawson (2003). Perseus, ed. Mathematical Traveler: Exploring the Grand History of Numbers. p. 187. ISBN 0-7382-0835-3.
- ↑ John Horton Conway, Richard K. Guy (1995). Copernicus, ed. The Book of Numbers. p. 242. ISBN 0-387-97993-X.
- ↑ Xavier Gourdon, Pascal Sebah. Collection of series for Pi.
- ↑ R. A. Knoebel. Exponentials Reiterated. Maa.org.
- ↑ Renzo Sprugnoli. Universita di Firenze, ed. Introduzione alla Matematica.
- ↑ Andrei Vernescu. Constante de tip Euler generalizate.
- ↑ Eric W. Weisstein (2002). CRC Press, ed. CRC Concise Encyclopedia of Mathematics, Second Edition. p. 1356.
- ↑ T. Piezas. Tribonacci constant & Pi.
- ↑ Clifford A. Pickover (2005). John Wiley & Sons, Inc., ed. A Passion for Mathematics. p. 90. ISBN 978-0-471-69098-6.
- ↑ Eric Weisstein. The square root of i..
- ↑ J. Sondow. Generalization of Somos Quadratic.
- ↑ Jesus Guillera and Jonathan Sondow. arxiv.org, ed. Double integrals and infinite products....
- ↑ Andras Bezdek (2003). Marcel Dekkcr, Inc., ed. Discrete Geometry. p. 150. ISBN 0-8247-0968-3.
- ↑ Annie Cuyt, Viadis Brevik Petersen, Brigitte Verdonk, William B. Jones (2008). Springer, ed. Handbook of continued fractions for special functions. p. 190. ISBN 978-1-4020-6948-2.
- ↑ Simon Plouffe. Miscellaneous Mathematical Constants.
- ↑ Steven Finch. Harvard University, ed. Addenda to Mathematical Constants.
- ↑ Eric W. Weisstein (2003). CRC Concise Encyclopedia of Mathematics, Second Edition. CRC Press. p. 1688. ISBN 1-58488-347-2.
- ↑ Theo Kempermann (2005). Freiburger graphische betriebe, ed. Zahlentheoretische Kostproben. p. 139. ISBN 978-3-8171-1692-8.
- ↑ Steven Finch (2003). Cambridge University Press, ed. Mathematical Constants. p. 449. ISBN 978-0-521-81805-6.
- ↑ Edward Kasner y James Newman (2007). Matemáticas e imaginación. p. p.76. ISBN 978-970-35-1300-0.
- ↑ Bruce C. Berndt,Robert Alexander Rankin (2000). AMS, ed. Ramanujan: Essays and Surveys. p. 219. ISBN 0-8218-2624-7.
- ↑ PAJ Lewis (2008). Ratna-Sagar, ed. Essential Mathematics. p. p.24. ISBN 978-81-8332-367-3.
- ↑ Richard J. Mathar (2013). Circumscribed Regular Polygons. arxiv.org.
- ↑ Jan Feliksiak (2013). The Symphony of Primes, Distribution of Primes and Riemann’s Hypothesis. Xlibris Corporation. p. 18. ISBN 978-1-4797-6558-4.
- ↑ Refaat El Attar (2006). Lulu Press, ed. Special Functions And Orthogonal Polynomials. p. p.58. ISBN 1-4116-6690-9.
- ↑ H. M. Srivastava,Junesang Choi (2012). Zeta and q-Zeta Functions and Associated Series and Integrals. Elsevier. p. 613. ISBN 978-0-12-385218-2.
- ↑ M.R.Burns (1999). Root constant. http://marvinrayburns.com/.
- ↑ Richard E. Crandall (2012). Unified algorithms for polylogarithm, L-series, and zeta variants. http://www.perfscipress.com.
- ↑ RICHARD J. MATHAR (2010). NUMERICAL EVALUATION OF THE OSCILLATORY INTEGRAL. http://arxiv.org/abs/0912.3844.
- ↑ Steven Finch. Harvard University, ed. Volumes of Hyperbolic 3-Manifolds.
- ↑ J. Coates,Martin J. Taylor (1991). L-Functions and Arithmetic. Cambridge University Press. p. 333. ISBN 0-521-38619-5.
- ↑ Keith B. Oldham,Jan C. Myland,Jerome Spanier (2009). Springer, ed. An Atlas of Functions: With Equator, the Atlas Function Calculator. p. 15. ISBN 978-0-387-48806-6.
- ↑ David Darling (2004). Wiley & Sons inc., ed. The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes. p. 63. ISBN 0-471-27047-4.
- ↑ Dusko Letic, Nenad Cakic, Branko Davidovic and Ivana Berkovic. Springer, ed. Orthogonal and diagonal dimension fluxes of hyperspherical function.
- ↑ Lennart R©Æde,Bertil Westergren (2004). Mathematics Handbook for Science and Engineering. Springer-Verlag. p. 194. ISBN 3-540-21141-1.
- ↑ Julian Havil (2012). Princeton University Press, ed. The Irrationals: A Story of the Numbers You Can't Count On. p. 98. ISBN 978-0-691-14342-2.
- ↑ Keith J. Devlin (1999). Columbia University Press, ed. Mathematics: The New Golden Age. p. 66. ISBN 0-231-11638-1.
- ↑ M. B. Kanchi (2002). New Age International Ltd. Publishers, ed. Matrix Methods Of Structural Analysis. p. 231. ISBN 81-224-0429-5
|isbn=incorrecto (ayuda). - ↑ Andrija S. Radovic. A representation of factorial function, the natura of constat and a way for solving of functional equation F(x) = x . F(x - 1).
- ↑ Properties of the Lambert Function W(z).
- ↑ Properties of the Lambert function W(z).
- ↑ Julian Havil (2003). Princeton University Press, ed. Gamma: Exploring Euler's Constant. p. 64. ISBN 9780691141336.
- ↑ Paulo Ribenboim (2000). Springer-Verlag, ed. My Numbers, My Friends: Popular Lectures on Number Theory. p. 66. ISBN 0-387-98911-0.
- ↑ Paulo Ribenboim (2000). Springer, ed. My Numbers, My Friends: Popular Lectures on Number Theory. p. 66. ISBN 0-387-98911-0.
- ↑ Kathleen T. Alligood (1996). Springer, ed. Chaos: An Introduction to Dynamical Systems. p. 501. ISBN 0-387-94677-2.
- ↑ K. T. Chau,Zheng Wang (2011). John Wiley & Son, ed. Chaos in Electric Drive Systems: Analysis, Control and Application. p. 7. ISBN 978-0-470-82633-1.
- ↑ David Borwein, Jonathan M. Borwein, and Christopher Pinner (1998). Convergence of Madelung-Like Lattice sums. AMS. p. Volume 350, Number 8, Pages 3131-3167.
- ↑ Michael A. Idowu (2012). arXiv:1210.5559, ed. Fundamental relations between the Dirichlet beta function, euler numbers, and Riemann zeta function for positive integers. p. 1.
- ↑ Thomas Koshy (2007). Elsevier, ed. Elementary Number Theory with Applications. p. 119. ISBN 978-0-12-372-487-8.
- ↑ Pascal Sebah and Xavier Gourdon (2002). Introduction to twin primes and Brun’s constant computation.
- ↑ John Derbyshire (2003). Joseph Henry Press, ed. Prime Obsession: Bernhard Riemann and the Greatest unsolved problem. p. p.319. ISBN 0-309-08549-7.
- ↑ Michael Trott (2004). The Mathematica GuideBook for Programming. Springer Science. p. 173. ISBN 0-387-94282-3.
- ↑ James T. Smith (2000). John Wiley & Sons, ed. Methods of Geometry. p. 123. ISBN 0-471-25183-6.
- ↑ Michael Jacobson,Hugh Williams (2009). Springer, ed. Solving the Pell Equation. p. 159. ISBN 978-0-387-84922-5.
- ↑ Jonathan Sondowa, Diego Marques (2010). Annales Mathematicae, ed. Algebraic and transcendental solutions of some exponential equations.
- ↑ J.L. Berggren, Jonathan M. Borwein, Peter Borwein (2003). Springer-Verlag, ed. Pi: A Source Book. p. 637. ISBN 0-387-20571-3.
- ↑ Jorg Arndt,Christoph Haenel (2000). Verlag Berlin Heidelberg, ed. Pi -- Unleashed. p. 13. ISBN 3-540-66572-2.
- ↑ Eric W. Weisstein (2003). CRC Press, ed. CRC Concise Encyclopedia of Mathematics, Second Edition. p. 151. ISBN 1-58488-347-2.
- ↑ H. M. Srivastava, Junesang Choi (2012). Elsevier, ed. Zeta and q-Zeta Functions and Associated Series and Integrals. p. 2. ISBN 978-0-12-385218-2.
- ↑ Ivan Niven. Averages of exponents in factoring integers.
- ↑ D. R. Woodall (2005). University of Nottingham, ed. CHROMATIC POLYNOMIALS OF PLANE TRIANGULATIONS. p. 5.
- ↑ R. M. ABRAROV AND S. M. ABRAROV (2011). arxiv.org, ed. PROPERTIES AND APPLICATIONS OF THE PRIME DETECTING FUNCTION. p. 8.
- ↑ Howard Curtis (2014). Elsevier, ed. Orbital Mechanics for Engineering Students. p. 159. ISBN 978-0-08-097747-8.
- ↑ Lloyd N. Trefethen (2013). SIAM., ed. Approximation Theory and Approximation Practice. p. 211. ISBN 978-1-611972-39-9.
- ↑ William Dunham (2005). Princeton University Press, ed. The Calculus Gallery: Masterpieces from Newton to Lebesgue. p. 51. ISBN 978-0-691-09565-3.
- ↑ Jean Jacquelin (2010). SOPHOMORE'S DREAM FUNCTION.
- ↑ {Cita libro |autor= Mauro Fiorentini |título= Nielsen – Ramanujan (costanti di) |url= http://bitman.name/math/article/872 }}
- ↑ Lennart Råde,Bertil (2000). Springer-Verlag, ed. Mathematics Handbook for Science and Engineering. p. p.423. ISBN 3-540-21141-1.
- ↑ Henri Cohen (2000). Springer, ed. Number Theory: Volume II: Analytic and Modern Tools. p. 127. ISBN 978-0-387-49893-5.
- ↑ H. M. Srivastava,Choi Junesang (2001). Kluwer Academic Publishers, ed. Series Associated With the Zeta and Related Functions. p. 30. ISBN 0-7923-7054-6.
- ↑ E. Catalan (1864). Kluwer Academic éditeurs, ed. Mémoire sur la transformation des séries, et sur quelques intégrales définies, Comptes rendus hebdomadaires des séances de l’Académie des sciences 59. p. 618.
- ↑ Bart Snapp (2012). Creative Commons, ed. Numbers and Algebra.
- ↑ George Gheverghese Joseph (2011). Princeton University Press, ed. The Crest of the Peacock: Non-European Roots of Mathematics. p. 295. ISBN 978-0-691-13526-7.
- ↑ DIVAKAR VISWANATH (1999). Mathematics of computation, ed. Random Fibonacci Sequences and the number 1.13198824....
- ↑ Annie Cuyt, Vigdis Brevik Petersen, Brigitte Verdonk, Haakon Waadelantl, William B. Jones. (2008). Springer, ed. Handbook of Continued Fractions for Special Functions. p. 188. ISBN 978-1-4020-6948-2.
- ↑ John Derbyshire (2003). Joseph Henry Press, ed. Prime Obsession: Bernhard Riemann and the Greatest unsolved problem. p. 147. ISBN 0-309-08549-7.
- ↑ Calvin C Clawson (2001). Mathematical sorcery: revealing the secrets of numbers. p. IV. ISBN 978 0 7382 0496-3.
- ↑ L. J. Lloyd James Peter Kilford (2008). Imperial College Press, ed. Modular Forms: A Classical and Computational Introduction. p. 107. ISBN 978-1-84816-213-6.
- ↑ Marek Wolf (2010). arxiv.org: 1003.4015, ed. Continued fractions constructed from prime numbers. p. 16.
- ↑ Eli Maor (1994). Princeton University Press, ed. "e": The Story of a Number. p. 37. ISBN 978-0-691-14134-3.
- ↑ Robin Whitty. Lieb’s Square Ice Theorem.
- ↑ Helmut Brass,Knut Petras (2010). AMS, ed. Quadrature Theory: The Theory of Numerical Integration on a Compact Interval. p. p.274. ISBN 978-0-8218-5361-0.
- ↑ Jvrg Arndt,Christoph Haenel. Springer, ed. Pi: Algorithmen, Computer, Arithmetik. p. 67. ISBN 3-540-66258-8.
- ↑ Reinhold Remmert (1991). Springer, ed. Theory of Complex Functions. p. 162. ISBN 0-387-97195-5.
- ↑ Eli Maor (2006). Princeton University Press, ed. e: The Story of a Number. ISBN 0-691-03390-0.
- ↑ James Stuart Tanton (2005). Encyclopedia of Mathematics. p. 529. ISBN 9781438110080.
- ↑ Manfred Robert Schroeder (2006). Springer-Verlag, ed. Number Theory in Science And Communication: With Applications in. p. p.68. ISBN 3-540-26596-1.
- ↑ Marek Wolf (2010). Instytut Fizyki Teoretycznej, ed. Two arguments that the nontrivial zeros of the Riemann zeta function are irrational.
- ↑ Timothy Gowers, June Barrow-Green, Imre Leade (2007). Princeton University Press, ed. The Princeton Companion to Mathematics. p. 316. ISBN 978-0-691-11880-2.
- ↑ A.A. Hattangadi (2000). Universities Press (India), ed. Explorations In Mathematics. p. p.39. ISBN 81-7371-387-1.
- ↑ Vijaya AV (2007). Figuring Out Mathematics. Dorling Kindcrsley (India) Pvt. Lid. p. 15. ISBN 978-81-317-0359-5.
- ↑ AARON HERSCHFELD (1935). ON INFINITE RADICALS. Columbia University, JSTOR. p. 419.
- ↑ Steven Finch (2014). Harvard.edu, ed. Errata and Addenda to Mathematical Constants. p. 59.
- ↑ Grupoalquerque. NÚMERO DE BRONCE. PROPORCIÓN DE BRONCE.
- ↑ H.M. Antia (2000). Birkhäuser Verlag, ed. Numerical Methods for Scientists and Engineers. p. 220. ISBN 3-7643-6715-6.
- ↑ David Cohen (2006). Thomson Learning Inc., ed. Precalculus: With Unit Circle Trigonometry. p. 328. ISBN 0-534-40230-5.
- ↑ Julian Havil (2003). Princeton University Press, ed. Gamma: Exploring Euler's Constant. p. 161. ISBN 9780691141336.
- ↑ Gérard P. Michon (2005). Numericana, ed. Numerical Constants.
- ↑ Ian Stewart (1996). Birkhäuser Verlag, ed. Professor Stewart's Cabinet of Mathematical Curiosities. ISBN 978-1-84765-128-0.
- ↑ Samuel W. Gilbert (2009). BookSurge, ed. The Riemann Hypothesis and the Roots of the Riemann Zeta Function. p. 93. ISBN 978-1439216385.
- ↑ «Round 2... 10 Trillion Digits of Pi» (en inglés). Consultado el 31 de agosto de 2012.
- ↑ A list of notable large computations of e
- ↑ a b c d e f g «Constant and Records of Computation (agosto 2010)» (en inglés). Consultado el 31 de marzo de 2011.
- ↑ sqrt(5) en www.goldenratio.org.
- ↑ a b Weisstein, Eric W. «Feigenbaum Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Sitio MathWorld Wolfram.com[editar]
- ↑ Weisstein, Eric W. «Erdos-Borwein Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Hypersphere Packing». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Erdos-Borwein Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «/Double Factorial». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Log Gamma Function». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «/Reuleaux Tetrahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Salem Constants». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Golden Angle». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Sylvester's Sequence». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Mandelbrot Set». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Exponential Factorial». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Smarandache Constants». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Lebesgue Constants». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Disk Covering Problem». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Komornik-Loreti Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Chebyshev Constants». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Chi». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Golomb-Dickman Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Reuleaux Triangle». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Self-Avoiding Walk Connective Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Du Bois Reymond Constants». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Twenty-Vertex Entropy Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Silverman Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Baxter's Four-Coloring Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Feller-Tornier Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Tetranacci Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Prince Rupert's Cube». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Plouffe's Constants». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Thue-Morse Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Pell Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Moving Sofa Problem». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Hermite Constants». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Cantor Set». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Hall-Montgomery Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Calabi's Triangle». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Lochs' Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Apollonian Gasket». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Heath-Brown-Moroz Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Plouffe's Constants». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Primorial». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Domino Tiling». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Sarnak's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «e». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Gauss-Kuzmin-Wirsing Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Conway's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Levy Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Kempner Series». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Lebesgue Constants». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Foias Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Foias Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Robbins Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Lüroth's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «TwinPrimes». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Lemniscate Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Stephen's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Dottie Number». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Taniguchi's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Golden Spiral». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Lemniscate Case». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Totient Summatory Function». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Ford Circle». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Riemann Zeta Function». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Backhouse's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Lebesgue Constants». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Alladi-Grinstead Constants». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Koch Snowflake». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Fibonacci Factorial Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Paper Folding Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Goh-Schmutz Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Bifoliate». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Dragon Curve». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Dragon Curve». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Mills Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Figure Eight Knot». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Porter's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Wilbraham-Gibbs Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Grothendieck's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Khinchin Harmonic Mean». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Trott Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Soldner's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Cahen's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Gausss Digamma Theorem». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Carlson-Levin Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Copeland-Erdos Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Wallis's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Carefree Couple». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Omega Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Landau Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Polya's Random Walk Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Hafner-Sarnak-McCurley Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Renyi's Parking Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Relatively Prime». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Champernowne Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Landau-Ramanujan Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Pascal's Triangle». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Liouville's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Power Tower». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Sierpinski Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Power Tower». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ (en inglés)Paper Folding Constant
- ↑ Weisstein, Eric W. «Somos's Quadratic Recurrence Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Gompertz Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «ContinuedFraction Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Masser-Gramain Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «e». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Gaussian Sum». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Paris Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Polygon Inscribing». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Glaisher-Kinkelin Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Gamma Function». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Euler-Mascheroni Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «MRB Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Gieseking's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Lemniscate Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Gauss's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Chaitin's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Fransen-Robinson Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Riemann Zeta Function». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «i». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «PowerTower». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Mertens Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «PrimeFormulas». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Artin's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Feigenbaum Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Feigenbaum Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Madelung Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Brun's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Brun's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Pi Formulas». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Tree Searching». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Power Tower». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Plouffe's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Prime Products». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Weierstrass Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Euler-Mascheroni Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Niven's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Central Binomial Coefficient». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Silver Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Natural Logarithm of 2». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Twin Primes Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Laplace Limit». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Bernstein´s Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Sophomore's Dream Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Sophomore's Dream». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Nielsen-Ramanujan Constants». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Dirichlet Beta Function». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Catalan's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Random Fibonacci Sequence». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Apery's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Gamma Function». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Delian Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Pythagoras's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Ramanujan Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Hyperbolic Tangent». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Factorial Sums». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Liebs Square Ice Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Favard Constants». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «i». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Steiner's Problem». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Wallis Formula». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Levy Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Golden Ratio». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Riemann Zeta Function Zeta 2». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Theodorus's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Nested Radical Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Universal Parabolic Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Silver Ratio». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Gelfond-Schneider Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Khinchin's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Reciprocal Fibonacci Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ Weisstein, Eric W. «Plastic Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- ↑ (en inglés)Weisstein, Eric W. «Gelfond's Constant». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Sitio OEIS Wiki[editar]
- ↑ [https://arxiv.org/abs/0905.0163
- ↑ Analog of the series MRB constant
- ↑ Double factorial
- ↑ Iterated logarithm
- ↑ (en inglés)Reciprocal of the Euler–Mascheroni constant
- ↑ (en inglés)Sqrt(e)
- ↑ (en inglés)Buffon's constant
- ↑ (en inglés)Roots and powers of 2
Enlaces externos[editar]
- Inverse Symbolic Calculator, Plouffe's Inverter
- Tablas de decimales de constantes en http://www.gutenberg.org.
- Miscellaneous Mathematical Constants - 170000 digits of Euler or gamma.
- On-Line Encyclopedia of Integer Sequences (OEIS)
- Simon Plouffe, Tables of Constants
- Simon Plouffe, Inverse Symbolic Calculator
- Xavier Gourdon and Pascal Sebah's page of numbers, mathematical constants and algorithms
- MathConstants
- Weisstein, Eric W. «Constants - from Wolfram MathWorld». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.




![{\displaystyle {\frac {1+{\sqrt[{3}]{\frac {29+3{\sqrt {93}}}{2}}}+{\sqrt[{3}]{\frac {29-3{\sqrt {93}}}{2}}}}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3510de22f4cf5ef7ee75a3f8a20a420cbd5af61)








![{\displaystyle \lim _{n\rightarrow \infty }\int _{1}^{2n}(-1)^{x}~{\sqrt[{x}]{x}}~dx=\int _{1}^{2n}e^{i\pi x}~x^{1/x}~dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8a5f7620cf389898c275ed984f8688bbdf200b1)

![{\displaystyle \sum _{n=0}^{\infty }{\frac {1}{n!!}}={\sqrt {e}}\left[{\frac {1}{\sqrt {2}}}+\gamma ({\tfrac {1}{2}},{\tfrac {1}{2}})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e51ab5b1eae938ed34d7dd811be48e359de7b97)






















































































































![{\displaystyle {\frac {[\Gamma ({\tfrac {1}{4}})]^{2}}{\sqrt {2\pi }}}=4\int _{0}^{1}{\frac {dx}{\sqrt {(1-x^{2})(2-x^{2})}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838230a1a8781844335c2977f729a38f594a7da6)




















![{\displaystyle {\sqrt[{4}]{5}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ca317d0c75e7b6f908151e893d8a05f990ee060)
![{\displaystyle {\sqrt[{5}]{5\,{\sqrt[{5}]{5\,{\sqrt[{5}]{5\,{\sqrt[{5}]{5\,{\sqrt[{5}]{5\,\cdots }}}}}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3127d3db98c6e81870992019a1d56264a39f7a90)













![{\displaystyle \prod _{n=1}^{\infty }{\frac {n!}{{\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}{\sqrt[{12}]{1+{\tfrac {1}{n}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81ce7cd71c37a3c97c3b4244332953b626c26900)












![{\displaystyle {\sqrt[{3}]{1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/911022b24127c88770950e9ebfe48fbd12d3fddf)








![{\displaystyle {\frac {\log \left({\frac {1+{\sqrt[{3}]{73-6{\sqrt {87}}}}+{\sqrt[{3}]{73+6{\sqrt {87}}}}}{3}}\right)}{\log(2)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a4162d90ad47ab451e6a198868b1d38f9a4f305)















![{\displaystyle \textstyle [1,0,8,4,1,0,1,5,1,2,2,3,1,1,1,3,6,...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b68851379d89009d2aa551f5f625d15a16c033f)













![{\displaystyle {\sqrt[{3}]{\frac {45-{\sqrt {1929}}}{18}}}+{\sqrt[{3}]{\frac {45+{\sqrt {1929}}}{18}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4a477d1c213e6e2b9bad2f5190a12810278e06a)










![{\displaystyle \prod _{k=1}^{\infty }\left\{1-\left[1-\prod _{j=1}^{n}(1-p_{k}^{-j})\right]^{2}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c604e073b81c602f0926f2a05bc337eea83dcfc)

























![{\displaystyle \textstyle {\frac {1+{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\sqrt[{3}]{19-3{\sqrt {33}}}}}{3}}=\scriptstyle \,1+\left({\sqrt[{3}]{{\tfrac {1}{2}}+{\sqrt[{3}]{{\tfrac {1}{2}}+{\sqrt[{3}]{{\tfrac {1}{2}}+...}}}}}}\right)^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dae9951b8fe98213be5c592eca8d81e10dcbc441)



![{\displaystyle {\sqrt[{4}]{-1}}={\frac {1+i}{\sqrt {2}}}=e^{\frac {i\pi }{4}}=\cos \left({\frac {\pi }{4}}\right)+i\sin \left({\frac {\pi }{4}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37c0f3410cad402cfea4cf785416d99e3b2f417d)

![{\displaystyle \prod _{n=1}^{\infty }n^{{3}^{-n}}={\sqrt[{3}]{1{\sqrt[{3}]{2{\sqrt[{3}]{3\cdots }}}}}}=1^{1/3}\;2^{1/9}\;3^{1/27}\cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9e06c4b0df773f89d608077c7e00b4356a59994)

















![{\displaystyle 2\!\prod _{n=1}^{\infty }\!\!\textstyle {\sqrt[{2^{n}}]{\frac {\prod _{i=1}^{2^{n-1}}(2^{n}+2i)}{\prod _{i=1}^{2^{n-1}}\!(2^{n}+2i-1)}}}=2{\sqrt {\frac {4}{3}}}{\sqrt[{4}]{\frac {6\cdot 8}{5\cdot 7}}}{\sqrt[{8}]{\frac {10\cdot 12\cdot 14\cdot 16}{9\cdot 11\cdot 13\cdot 15}}}\cdots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6c0c981eac3e5b5b1d2f133e2e05b631a7d6d92)

















![{\displaystyle \sum _{n=1}^{\infty }({-}1)^{n}(n^{1/n}{-}1)=-{\sqrt[{1}]{1}}+{\sqrt[{2}]{2}}-{\sqrt[{3}]{3}}+{\sqrt[{4}]{4}}\,...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d24fe745eaaccd7b633f9fbe8f9f447729e1f17d)
















![{\displaystyle {\sqrt[{i}]{i}}=i^{-i}=i^{\frac {1}{i}}=(i^{i})^{-1}=e^{\frac {\pi }{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/904fff5ea95018fde18c45c94097a379edad291e)

















































![{\displaystyle 2+2\cos {\frac {2\pi }{7}}=\textstyle 2+{\frac {2+{\sqrt[{3}]{7+7{\sqrt[{3}]{7+7{\sqrt[{3}]{\,7+\cdots }}}}}}}{1+{\sqrt[{3}]{7+7{\sqrt[{3}]{7+7{\sqrt[{3}]{\,7+\cdots }}}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df4b6dfb762686eef1476628b27712ce19606c54)















![{\displaystyle {\sqrt[{12}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc835f27425fb3140e1f75a5faa35b1e8b9efc35)










![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)


















![{\displaystyle {\sqrt[{e}]{e}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96733766fde42bf61b329fba3cc27c54f46b21e5)











![{\displaystyle {\sqrt[{3}]{3\,{\sqrt[{3}]{3\,{\sqrt[{3}]{3\,{\sqrt[{3}]{3\,{\sqrt[{3}]{3\,\cdots }}}}}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6a7a7a3adada2776b2b2ade49205f1f22eafca1)












![{\displaystyle \prod _{n=1}^{\infty }\left[{1{+}{1 \over n(n{+}2)}}\right]^{\frac {\ln n}{\ln 2}}=\lim _{n\to \infty }\left(\prod _{k=1}^{n}a_{k}\right)^{\frac {1}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/527566b0fceb254898a4ff152297b8e0c5921ae6)


![{\displaystyle \textstyle {\sqrt[{3}]{1{+}{\sqrt[{3}]{1{+}{\sqrt[{3}]{1{+}\cdots }}}}}}={\sqrt[{3}]{{\frac {1}{2}}+{\frac {1}{6}}{\sqrt {\frac {23}{3}}}}}+{\sqrt[{3}]{{\frac {1}{2}}-{\frac {1}{6}}{\sqrt {\frac {23}{3}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/971c5e9de7ce0ab9336ef8da0dd6591aede8f98d)






![{\displaystyle \gamma =\lim _{n\rightarrow \infty }\left[\sum _{k=1}^{n}{\frac {1}{k}}-\ln(n)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8569bc7e2125dd8b06ab300011c683a0d82147e)




