Análisis de circuitos

Un circuito eléctrico es un grupo de componentes interconectados. El análisis de circuitos es el proceso de calcular los diferentes parámetros del circuito como lo son: intensidades, tensiones o potencias. Existen muchas técnicas para lograrlo, Sin embargo, se asume que los componentes de los circuitos son lineales. Los métodos descritos en este artículo solo se aplican al análisis de circuitos lineales salvo en los casos expresamente establecidos. Para entender este artículo se necesitan saber las partes básicas de un circuito así como sus leyes fundamentales.
Definiciones[editar]
| Componente | Un dispositivo con dos o más terminales capaz de hacer fluir carga. |
| Nodo | Punto donde dos o más elementos tienen una conexión común. Se considera un nodo a un conductor con una resistencia igual a cero. |
| Rama | Una rama es un conjunto de elementos que se pueden simplificar formando un dispositivo que represente el comportamiento de ellos. |
| Malla | Cualquier circuito cerrado de ramas es una malla, con la condición que no pase dos veces por el mismo nodo. |
| Circuito | Red donde circula una corriente proveniente de una fuente, a través de componentes pasivos. Un circuito es, en este sentido, una red de dos terminales que sea trivial analizarse. Frecuentemente, "circuito" y "red" se usan indistintamente, pero muchos analistas reservan "red" para referirse a un modelo idealizado consistente de componentes ideales.[1] |
| Función de transferencia | La relación de las corrientes y tensiones de dos puertos. Se define frecuentemente como una comparación entre un puerto de entrada y un puerto de salida para determinar ganancia o atenuación. |
Circuitos equivalentes[editar]

Un procedimiento muy útil en el análisis de circuitos es simplificar el circuito al reducir su número de componentes. Esto se puede hacer al reemplazar los componentes actuales con otros componentes mucho más sencillos y que produzcan el mismo efecto. Una técnica particular podría reducir directamente el número de componentes, por ejemplo al combinar las resistencias en serie. Por otro lado, se podría simplemente cambiar la forma en que está conectado un componente para posteriormente reducir el circuito de una manera más fácil. Por ejemplo, Se podría transformar una fuente de tensión por una fuente de corriente usando el teorema de Norton para que después se pueda combinar la resistencia interna de la fuente con las resistencias en paralelo de un circuito.
Un circuito resistivo es un circuito compuesto de solo resistores, fuentes de corriente ideales, y fuentes de tensión ideales. Si las fuentes son constantes, el resultado es un circuito de corriente continua. El análisis de circuitos es el proceso de resolver las tensiones y corrientes presentes en un circuito. Los principios para solucionar un circuito resumidos aquí también se pueden aplicar para el análisis de fasores de circuitos de corriente alterna.
Se dice que dos circuitos son equivalentes respecto a una pareja de terminales cuando la tensión y la corriente que fluye a través de ellos son iguales.
si implica para todos los valores reales de , para las terminales ab y xy, entonces circuit 1 y circuit 2 son equivalentes
Lo anterior es la definición de circuitos de dos terminales. Para circuitos de más de dos terminales, las tensiones y corrientes de todos los terminales deben mantener la misma relación. Por ejemplo, los circuitos estrella y delta son circuitos de seis terminales y por lo tanto requieren tres ecuaciones simultáneas para especificar completamente su equivalencia.
Impedancias en serie y en paralelo[editar]
Cualquier circuito de dos terminales puede reducirse a una simple impedancia sumando las que se encuentran en serie o en paralelo, así:
- Impedancias en serie:
- Impedancias en paralelo:
Transformación estrella-triángulo[editar]

Una red eléctrica de impedancias con más de dos terminales no puede reducirse a un circuito equivalente de una sola impedancia. Una red de n terminales puede, como máximo, reducirse a n impedancias. Para una red de tres terminales, las tres impedancias pueden expresarse como un red delta (Δ) de tres nodos o una red estrella (Y) de cuatro nodos. Estas dos redes son equivalentes y las transformaciones de cada una de ellas son expresadas más abajo. Una red general con un número arbitrario de terminales no puede reducirse al mínimo número de impedancias usando solamente combinaciones en serie o en paralelo. En general, se deben usar las transformaciones Y-Δ y Δ-Y. Puede demostrarse que esto bastará para encontrar la red más simplificada para cualquier red arbitraria con aplicaciones sucesivas en serie, paralelo, Y-Δ y Δ-Y. No se requieren transformaciones más complejas.
Ecuaciones para la transformación Delta-Estrella[editar]
Ecuaciones para la transformación Estrella-Delta[editar]
Forma general de la eliminación de nodos en la red[editar]
Las transformaciones estrella-triángulo y triángulo-estrella son casos especiales del algoritmo general de la eliminación de nodos de una red resistiva. Cualquier nodo conectado por N resistores 1 .... N pueden reemplazarse por resistores conectados en los N nodos restantes. La resistencia entre cualquier nodo x e y está dada por:
Para una estrella-triángulo (N=3) se reduce a:
Para una reducción en serie (N=2) se reduce a:
Transformación de fuentes[editar]

Una fuente no ideal con una impedancia interna puede representarse como una fuente de tensión ideal o una fuente de corriente ideal más la impedancia. Estas dos formas son equivalentes y las transformaciones son dadas a continuación. Si las dos redes son equivalentes con respecto a las terminales ab, entonces V e I deben ser idénticas para ambas redes. Además,
- o
- El teorema de Norton establece que cualquier red de dos terminales puede reducirse a una fuente ideal de corriente y a una resistencia en paralelo.
- El teorema de Thévenin establece que cualquier red de dos terminales puede reducirse a una fuente ideal de tensión y a una resistencia en serie.
Redes simples[editar]
Algunos circuitos sencillos pueden analizarse sin la necesidad de aplicar métodos de análisis.
Divisor de tensión[editar]
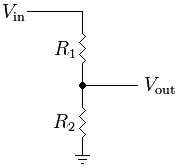
Dos o más resistencias conectadas en serie forman un divisor de tensión. De acuerdo con la segunda ley de Kirchhoff o ley de las mallas, la tensión total es suma de las tensiones parciales en cada resistencia, por lo que seleccionando valores adecuados de las mismas, se puede dividir una tensión en los valores más pequeños que se deseen. La tensión en bornes de la resistencia , en un divisor de tensión de n resistencias cuya tensión total es V, viene dada por:
En el caso particular de un divisor de dos resistencias, es posible determinar las tensiones en bornes de cada resistencia, VAB y VBC, en función de la tensión total, VAC, sin tener que calcular previamente la intensidad. Para ello se utilizan las siguientes ecuaciones de fácil deducción:
Divisor de corriente[editar]
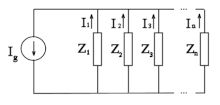
Dos o más resistencias conectadas en paralelo forman un divisor de intensidad. De acuerdo con la primera ley de Kirchhoff o ley de los nodos, la suma de las corrientes que entran en un nodo es igual a la suma de las corrientes que salen. Seleccionando valores adecuados de resistencias se puede dividir una corriente en los valores más pequeños que se deseen.
En el caso particular de un divisor de dos resistencias, es posible determinar las corrientes parciales que circulan por cada resistencia, I1 e I2, en función de la corriente total, I, sin tener que calcular previamente la caída de tensión en la asociación. Para ello se utilizan las siguientes ecuaciones de fácil deducción:
Análisis de nodos[editar]

- Marque todos los nodos en el circuito. Seleccione arbitrariamente cualquier nodo como de referencia.
- Defina una variable de tensión para todos los nodos restantes. Estas variables de tensión deben definirse como la tensión con respecto al nodo de referencia.
- Escriba una ecuación aplicando LCK para cualquier nodo excepto el de referencia.
- Resuelva el sistema de ecuaciones resultante.
Análisis de mallas[editar]
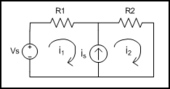
- Cuente el número de mallas existentes en el circuito. Asigne una corriente de malla a cada una de ellas.
- Escriba una ecuación LVK para cualquier malla cuya corriente sea desconocida.
- Resuelva las ecuaciones resultantes.
Superposición[editar]
En este método, se calcula el efecto de cada fuente por separado. Al analizar una fuente, se reemplazan las fuentes restantes por un cortocircuito para las fuentes de tensión o por un circuito abierto para las fuentes de corriente. La corriente que fluye en el componente o la tensión del componente es calculada al sumar todas las tensiones y corrientes individuales.
Este método funciona siempre y cuando se usen componentes lineales en el circuito. Nótese que para calcular los valores de cada fuente también se pueden usar análisis de malla y de nodos.
Elegir el método[editar]
Elegir el método adecuado necesita un poco de experiencia. Si el circuito es muy sencillo y solo se necesita calcular una tensión o una corriente entonces aplicando alguno de los dos métodos de redes simples podría resolverlo sin requerir a métodos más complicados.
- El Teorema de superposición es probablemente el método más sencillo pero se necesitan muchas más ecuaciones y muchas combinaciones de impedancias alargando mucho más el problema.
- Análisis de nodos: El número de variables de tensiones y del sistema de ecuaciones a resolver es igual al número de nodos menos uno. Toda fuente de tensión conectada al nodo de referencia reduce el número de variables desconocidas. Este método es muy útil cuando el circuito tiene fuentes de tensión.
- Análisis de malla: El número de las variables de corriente y del sistema de ecuaciones a resolver es igual al número de mallas. Cualquier fuente de corriente conectada en una malla reduce el número de variables desconocidas. Sin embargo, este método no se puede usar cuando el circuito no se pueda dibujar en un circuito plano de forma que ninguna rama se cruce con la otra. Este método es muy efectivo cuando el circuito tiene fuentes de corriente.
Funciones de transferencia[editar]
Una función de transferencia expresa la relación entre un valor de entrada y un valor de salida en un circuito. En los circuitos resistivos, siempre será un número real o una expresión que se puede reducir a un número real. Estos circuitos se representan por un sistema algebraico de ecuaciones. Sin embargo, para el caso general de las redes lineales, los circuitos se representan por un sistema de ecuaciones diferenciales lineales. En el análisis de circuitos, en vez de usar directamente las ecuaciones diferenciales, se prefiere usar la transformada de Laplace para así expresar los resultados en términos del parámetro de Laplace, que por lo general es complejo.
Esta aproximación es base para la teoría de control y es útil para determinar la estabilidad de un sistema.
Funciones de transferencia para componentes de dos terminales[editar]
Para componentes de dos terminales la función de transferencia, llamada también ecuación constitutiva, es la relación entre la corriente de entrada del dispositivo y la tensión resultante del componente. La función de transferencia Z(s) será la impedancia y tendrá unidades en ohms.
- Para los tres componentes pasivos que se encuentran en los circuitos eléctricos, las funciones de transferencia son en corriente alterna y corriente directa las siguientes:
| Componente | Función de transferencia | Corriente Alterna | Corriente Directa |
|---|---|---|---|
Funciones de transferencia para redes de dos puertos[editar]
Las funciones de transferencia, en teoría de control, son dadas por el símbolo H(s). Frecuentemente en electrónica la función de transferencia se define como la relación del voltaje de salida al voltaje de entrada y dado el símbolo A(s), o más general (porque el análisis es invariable en términos de la respuesta del seno) A(jω), así:
Donde A representa la atenuación, ganancia, o amplificación dependiendo del contexto. En general, esto será una función compleja de jω, que se puede derivar del análisis de impedancias en la red y sus funciones de transferencia individuales. Algunas veces se está interesado solamente en la magnitud de la ganancia y no en el ángulo de fase. Para este caso se pueden eliminar los números complejos de la función de transferencia que podría escribirse así:
Parámetros de un circuito de dos puertos[editar]
El concepto de una red de dos puertos o cuadripolo puede ser útil en análisis de redes como una caja negra en el análisis. El comportamiento de las redes cuadripolo en una gran red puede caracterizarse completamente sin mantener nada de la estructura interna. Sin embargo, para hacer esto es necesario tener más información que el A(jω) descrito más arriba. Puede demostrarse que se requieren 4 parámetros para caracterizar completamente la red cuadripolo. Esto puede ser la función de transferencia directa, la impedancia de entrada, la función de transferencia inversa(por ejemplo, el voltaje que hay en la entrada cuando un voltaje se aplica a la salida) y la impedancia de salida. Hay muchas otras (véase el artículo principal para una lista completa), una de estas expresa todos los cuatro parámetros como impedancias. Es normal expresar los cuatro parámetros como una matriz.
La matriz puede abreviarse a un elemento representativo;
or just
Estos conceptos pueden extenderse a las redes de más de dos puertos. Sin embargo, es muy raro hacerlo en la realidad debido a que en muchos casos los puertos se consideran como una entrada o una salida. Si las funciones de transferencia inversa se ignoran, una red multipuerto puede siempre descomponerse en una red de dos puertos.
Componentes distribuidos[editar]
Donde una red se compone de componentes discretos, el análisis usando solamente redes cuadripolo, no es esencial. La red siempre puede analizarse en términos de sus funciones de transferencia individuales. Sin embargo, si una red contiene componentes distribuidos, como es el caso de una línea de transmisión, no es posible analizarse en términos de los componentes individuales puesto que no existen. La aproximación más usada a esto es modelar la línea como una red de dos puertos y caracterizarla usando parámetros de dos puertos (o algo equivalente a esto). Otro ejemplo de esta técnica es modelar las cargas cruzando la región base en un transistor de alta frecuencia. La región base debe modelarse como una resistencia distribuida y la capacitancia como un modelo simplificado.
Redes no lineales[editar]

Muchos de los diseños electrónicos son, en realidad, no lineales. De hecho, la mayoría de los semiconductores son no lineales. Indiferentemente del circuito no lineal, la función de transferencia de un semiconductor pn ideal es dada por la siguiente relación no lineal:
donde:
- i y v son la corriente instantánea y la tensión.
- Io es un parámetro arbitrario llamado la corriente de fuga inverso cuyo valor depende de la construcción del dispositivo.
- VT es un parámetro proporcional llamado tensión térmica y que es igual a 25mV a temperatura ambiente.
Hay muchas formas de no linealidad. Todos los métodos que usan superposiciones lineales fallan cuando están presentes componentes no lineales. Hay muchas opciones para tratar la no linealidad dependiendo del tipo del circuito y de la información que el analista desea obtener.
Véase también[editar]
- Leyes de Kirchhoff
- Análisis de malla
- Ley de Ohm
- Circuito serie
- Circuito paralelo
- Teorema de Tellegen
- Cuadripolo
- Teorema de Kennelly
Referencias[editar]
- ↑ Belevitch V (mayo de 1962). «Summary of the history of circuit theory». Proceedings of the IRE 50 (5): 849. doi:10.1109/JRPROC.1962.288301. cites «IRE Standards on Circuits: Definitions of Terms for Linear Passive Reciprocal Time Invariant Networks, 1960». Proceedings of the IRE 48 (9): 1609. septiembre de 1960. doi:10.1109/JRPROC.1960.287676.to justify this definition.
Sidney Darlington Darlington S (1984). «A history of network synthesis and filter theory for circuits composed of resistors, inductors, and capacitors». IEEE Trans. Circuits and Systems 31 (1): 4.
follows Belevitch but notes there are now also many colloquial uses of "network".





































![{\displaystyle \left[z(j\omega )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10811182bc24215e2eb8f5675f205548a9dc10a4)
![{\displaystyle \left[z\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1602ad8f429c7bdd31909a2c96547ada8d4d3f36)
